🎲 [ICLR 2025] DICE: 去中心化学习中的数据影响级联

朱通天

TongtianZhu

关注

标签： 数据_影响，去中心化_学习

作者：   朱通天¹    李文豪¹    王灿¹    何凤祥²

¹浙江大学      ²爱丁堡大学

📄 Openreview • 💻 代码 • 📚 arXiv • 🔗 Twitter • 🖼️ 海报 • 📊 幻灯片 • 🎥 视频 (中文)

更新中。更多内容即将推出！😉

🗓️ 2025-07-17 — 更新了主要结果

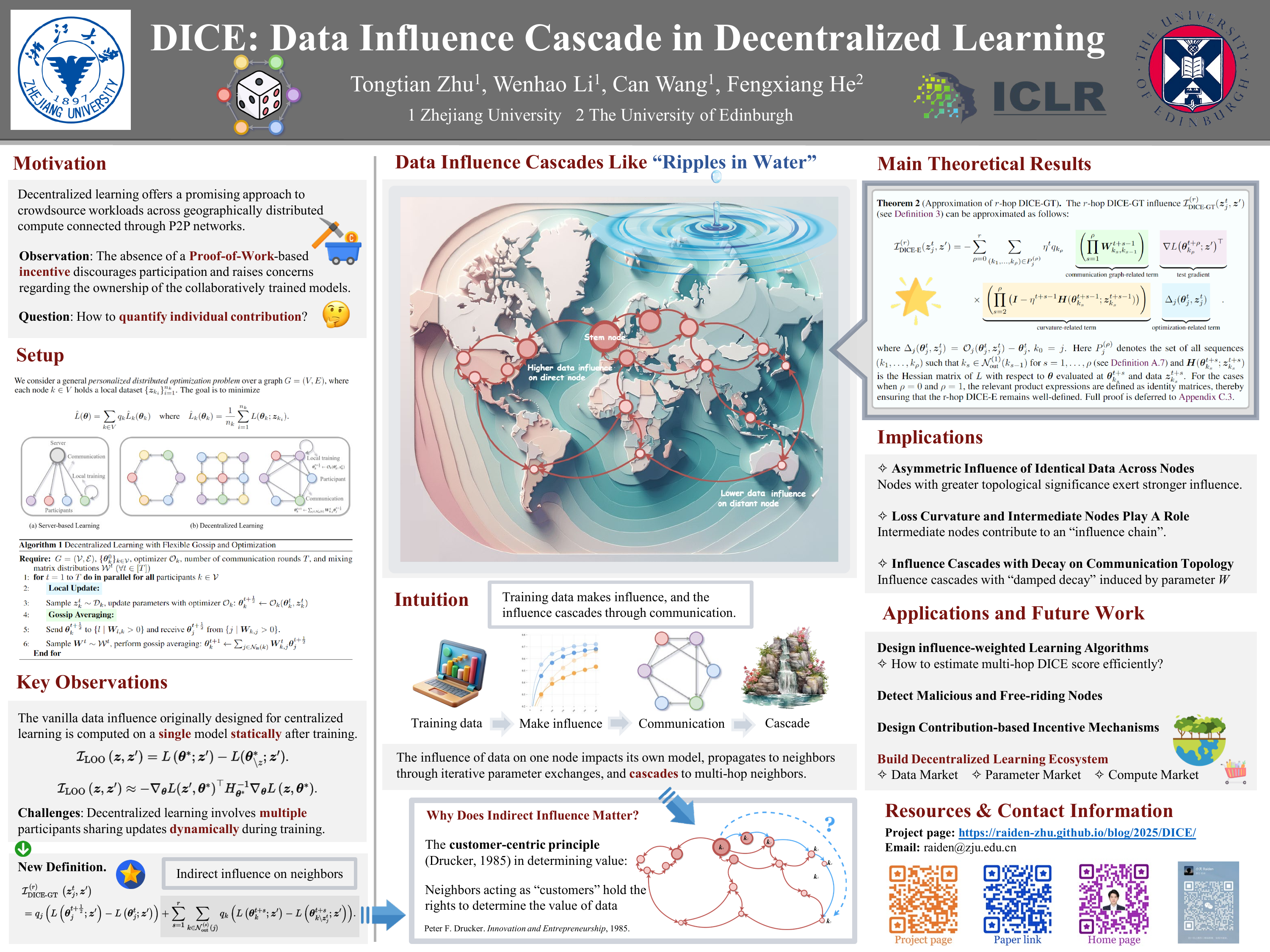
主要成果

定理 (r-跳 DICE-GT 的近似)

r-跳 DICE-GT 影响 ${\mathcal{I}}_{\mathrm{D}\mathrm{I}\mathrm{C}\mathrm{E}-\mathrm{G}\mathrm{T}}^{(r)}({\mathit{z}}_j^t,{\mathit{z}}^{\mathrm{\prime }})\backslash mathcal\{I\}\_\{\backslash mathrm\{DICE-GT\}\}^\{(r)\}(\backslash boldsymbol\{z\}\_j^t,\; \backslash boldsymbol\{z\}^\{\backslash prime\})$ 可近似如下

$$\begin{array}{cccc}& {\displaystyle \begin{array}{cc}{\displaystyle }& {\displaystyle {\mathcal{I}}_{\mathrm{D}\mathrm{I}\mathrm{C}\mathrm{E}-\mathrm{E}}^{(r)}({\mathit{z}}_j^t,{\mathit{z}}^{\mathrm{\prime }})}\\ {\displaystyle }& {\displaystyle =-\sum _{\rho =0}^r\sum _{(k_1,\dots ,k_{\rho })\in P_j^{(\rho )}}{\eta }^t{q}_{k_{\rho }}\underset{\text{communication graph-related term}}{\underbrace{\left(\prod _{s=1}^{\rho }{\mathit{W}}_{k_s,k_{s-1}}^{t+s-1}\right)}}\times \underset{\text{test gradient}}{\underbrace{\mathrm{\nabla }L({\mathit{\theta }}_{k_{\rho }}^{t+\rho };{\mathit{z}}^{\mathrm{\prime }}{)}^{\mathrm{\top }}}}}\\ {\displaystyle }& {\displaystyle \times \underset{\text{curvature-related term}}{\underbrace{\left(\prod _{s=2}^{\rho }(\mathit{I}-{\eta }^{t+s-1}\mathit{H}({\mathit{\theta }}_{k_s}^{t+s-1};{\mathit{z}}_{k_s}^{t+s-1}))\right)}}\times \underset{\text{optimization-related term}}{\underbrace{{\mathrm{\Delta }}_j({\mathit{\theta }}_j^t,{\mathit{z}}_j^t)}}}\end{array}}& & \end{array}$$

其中 ${\mathrm{\Delta }}_j({\mathit{\theta }}_j^t,{\mathit{z}}_j^t)={\mathcal{O}}_j({\mathit{\theta }}_j^t,{\mathit{z}}_j^t)-{\mathit{\theta }}_j^t\backslash Delta\_j(\backslash boldsymbol\{\backslash theta\}\_j^t,\backslash boldsymbol\{z\}\_j^t)\; =\; \backslash mathcal\{O\}\_j(\backslash boldsymbol\{\backslash theta\}\_j^t,\backslash boldsymbol\{z\}\_j^t)-\backslash boldsymbol\{\backslash theta\}\_j^t$, $k_0=jk\_0\; =\; j$。这里 $P_j^{(\rho )}P\_j^\{(\backslash rho)\}$ 表示所有序列 $(k_1,\dots ,k_{\rho })(k\_1,\; \backslash dots,\; k\_\{\backslash rho\})$ 的集合，使得 $k_s\in {\mathcal{N}}_{\mathrm{o}\mathrm{u}\mathrm{t}}^{(1)}(k_{s-1})k\_s\; \backslash in\; \backslash mathcal\{N\}\_\{\backslash mathrm\{out\}\}^\{(1)\}(k\_\{s-1\})$ 对于 $s=1,\dots ,\rho s=1,\backslash dots,\backslash rho$ 且 $\mathit{H}({\mathit{\theta }}_{k_s}^{t+s};{\mathit{z}}_{k_s}^{t+s})\backslash boldsymbol\{H\}(\backslash boldsymbol\{\backslash theta\}\_\{k\_s\}^\{t+s\};\; \backslash boldsymbol\{z\}\_\{k\_s\}^\{t+s\})$ 是 $LL$ 相对于 $\mathit{\theta }\backslash boldsymbol\{\backslash theta\}$ 在 ${\mathit{\theta }}_{k_s}^{t+s}\backslash boldsymbol\{\backslash theta\}\_\{k\_s\}^\{t+s\}$ 和数据 ${\mathit{z}}_{k_s}^{t+s}\backslash boldsymbol\{z\}\_\{k\_s\}^\{t+s\}$ 处的Hessian矩阵。

对于 $\rho =0\backslash rho\; =\; 0$ 和 $\rho =1\backslash rho\; =\; 1$ 的情况，相关乘积表达式被定义为单位矩阵，从而确保 r-跳 DICE-E 仍然是良好定义的。

引用

@inproceedings{zhu2025dice,
  title="{DICE: Data Influence Cascade in Decentralized Learning}",
  author="Tongtian Zhu and Wenhao Li and Can Wang and Fengxiang He",
  booktitle="The Thirteenth International Conference on Learning Representations",
  year="2025",
  url="[https://openreview.net/forum?id=2TIYkqieKw](https://openreview.net/forum?id=2TIYkqieKw)"
}