什么是 Transformer？
动机
小时候，我被科技及其带来的创新深深吸引。我特别感兴趣的一个领域是人工智能 (AI) 的基础，以及其子集机器学习 (ML)。带着这份新热情，我通过构建卷积神经网络 (CNN) 了解了计算机视觉 (CV) 以及计算机是如何“看到”的。通过训练强化学习 (RL) 模型，我对自动驾驶汽车如何导航有了直观的理解。现在，我偶然发现了《Attention Is All You Need》这篇论文，这促使我深入探索计算机如何对语言进行建模。
深入研究这篇论文后，它所奠定的基础及其对深度学习未来的影响令我印象深刻。论文中提出的细微之处具有变革性，为强大的大型语言模型 (LLM) 铺平了道路，例如：GPT-2 和 3、BERT、XLNET、编码助手 GitHub Copilot 以及非常著名的 ChatGPT。在我撰写本文时，LLM 已在我们的工作流程中占据主导地位，它们减少了研究时间，帮助我们调试代码，有时甚至完成了我们的作业……基于这些可能性和我的好奇心，我接受了构建这些模型背后的架构——Transformer——的挑战。
这项任务相当困难，对该主题知识的完善耗费了数月时间，但构建原始的序列到序列 Transformer 让我对 LLM 及其在未来 AI 中的重要性有了更深入的理解。最终，我希望不仅能向您展示如何构建 Transformer，还能让您对您的努力产生这个项目带给我的同样热情。
先决条件
鉴于这个主题相对高级，我假定您有一定的编程经验，并且对 AI 背后的技术方面有基本的了解。由于我们将使用 PyTorch，因此建议您也具备使用此 Python 框架的背景知识。接下来，我们将介绍许多概念和术语；如果您不熟悉，我在下面提供了复习资料，以帮助您理解我们将讨论的一些主题。
Transformer 解释
首先，Transformer 是一种深度神经网络，用于学习各种序列到序列任务（如语言翻译）中输入序列（源）和输出序列（目标）之间的关系。它利用词元（嵌入）的隐藏表示、词元在序列中的位置（位置编码）、词元之间上下文相关性（注意力机制）、非线性关系（位置级前馈网络）以及其他一些深度学习技术（例如归一化、正则化等）来执行此任务。这种方法不仅使 Transformer 成为 NLP 任务的最新（SOTA）架构，而且还解决了旧 NLP 架构（如 RNN）的一些缺陷。
注意：为方便日后参考，我交替使用“词元”和“词”，但两者含义不同。词元可以被认为是词或子词（例如，“learning”被词元化为“learn”和“ing”）。如果您对词元化感到好奇，可以从 huggingface nlp 课程中了解更多信息。
编码器-解码器架构
在 NMT 中，编码器-解码器架构是一种常见的实现方式，用于将输入序列转换为隐藏表示以进行翻译。在 Transformer 内部，编码器接收长度为 *n* 的输入词元序列 *xₙ*，并将其编码为隐藏表示 *zₙ*。接下来，解码器接收编码器的输出 *zₙ*，并将其解码为长度为 *m* 的输出词元序列 *yₘ*。这个过程是自回归的，因此解码器每次从编码器输出 *zₙ* 和之前预测的信息 *yₘ₋₁* 中预测一个词元。
Transformer 架构（左侧是编码器，右侧是解码器）嵌入
嵌入（Embeddings）是词元组成的序列转换为隐藏表示的重要部分。简单来说，嵌入将词语序列中的每个词映射成一系列值，这些值能最好地描述该词。每个词的值由嵌入权重分配，这些权重会随着嵌入层学习整个词汇表内词语之间的关系而改变（更多关于嵌入的信息请参阅本文）。
在“Attention Is All You Need”论文中，序列中的每个词元都将被嵌入到一个 512 维的向量中。（即 *dₘ = 512*）。展望未来，*dₘ* 是一个超参数，定义了 Transformer 隐藏表示的维度。在原始论文中，它被称为 *dmodel*，但我为了简化采用了我的符号。您会看到这个超参数在整个 Transformer 中重复使用，随着您阅读本博客，这会变得更有意义。
import torch.nn as nn
class Embeddings(nn.Module):
def __init__(self, vocab_size, dm, pad_id) -> None:
super().__init__()
self.embedding = nn.Embedding(vocab_size, dm, padding_idx=pad_id)
def forward(self, x):
# inshape: x - (batch_size, seq_len)
# embed tokens to dm | shape: out - (batch_size, seq_len, dm)
out = self.embedding(x)
return out
位置编码
现在，我们已经有了理解输入序列中词元含义的方法，接下来必须将它们彼此之间进行位置关联。这很重要，因为我们不会说“星球大战是史上最伟大的电影系列。”与“大战最伟大星球这部电影系列是时间最伟大的全部。”具有相同的含义，因此需要位置编码来捕获序列中词元的顺序。
由于 Transformer 模型不使用先前架构中用于位置关联词元的循环，因此使用正弦模式（即正弦和余弦函数）来编码序列中词元的位置。
位置编码函数编码首先根据序列的最大长度和模型的隐藏维度创建。接下来，上述方程允许通过正弦曲线映射词元的位置。`pos` 表示词在分词文本序列中的位置或索引，`i` 表示位置隐藏表示的索引，`d model` 是模型的隐藏维度；我们之前提到 `dₘ = 512`。
如果使用正弦函数绘制位置，不同的位置将由于函数的波浪状行为而具有不同的编码。尽管如此，一些具有不同位置的词元可能会得到相同的编码，因为正弦波会重复。为了抵消这种情况，`i` 用于为单个位置输出多个正弦曲线（频率），从而为序列中的每个词元提供唯一的编码。本质上，`i` 根据其值是偶数还是奇数创建交替的正弦和余弦波，从而使模型在训练期间更容易“通过相对位置进行注意”（此帖子中的视觉效果和更详细的解释）。
在处理输入时，位置编码器将嵌入和相应的位置编码相加，以捕获序列中词元的含义和顺序。
import torch
import torch.nn as nn
import numpy as np
class PositionalEncoder(nn.Module):
def __init__(self, dm, maxlen, dropout=0.1, scale=True) -> None:
super().__init__()
self.dm = dm
self.drop = nn.Dropout(dropout)
self.scale = scale
# shape: pos - (maxlen, 1) dim - (dm, )
pos = torch.arange(maxlen).float().unsqueeze(1)
dim = torch.arange(dm).float()
# apply pos / (10000^2*i / dm) -> use sin for even indices & cosine for odd indices
values = pos / torch.pow(1e4, 2 * torch.div(dim, 2, rounding_mode="floor") / dm)
encodings = torch.where(dim.long() % 2 == 0, torch.sin(values), torch.cos(values))
# reshape: encodings - (1, maxlen, dm)
encodings = encodings.unsqueeze(0)
# register encodings w/o grad
self.register_buffer("pos_encodings", encodings)
def forward(self, embeddings):
# inshape: embeddings - (batch_size, seq_len, dm)
# scale embeddings (if applicable)
if self.scale:
embeddings = embeddings * np.sqrt(self.dm)
# sum embeddings w/ respective positonal encodings | shape: embeddings - (batch_size, seq_len, dm)
seq_len = embeddings.size(1)
embeddings = embeddings + self.pos_encodings[:, :seq_len]
# drop neurons | out - (batch_size, seq_len, dm)
out = self.drop(embeddings)
return out
注意：在 Transformer 中，通常不仅将嵌入值乘以模型隐藏维度的平方根进行归一化，还通过使用 Dropout（即 *scale = sqrt(dₘ)* 和 *dropout = 0.1*）丢弃 10% 的值来进行正则化。这些组件的添加有助于模型的学习能力，并防止其在训练期间过拟合。
解释了嵌入和位置编码后，我们可以进一步探讨允许 Transformer 理解上下文信息的主要子层：注意力机制。
注意力
注意力是一种机制，它接受一个查询和一组键值对，并根据查询和键之间的相似性对值施加权重。从某种意义上说，注意力机制允许 Transformer 学习如何对序列进行上下文化，以及如何“翻译”这些上下文化后的序列。在 NMT 中，注意力有许多不同的实现，但在 Transformer 中，使用了缩放点积注意力。
缩放点积注意力
缩放点积注意力图和函数在缩放点积注意力中，我们计算查询（Q）和键（K）之间的点积，两者维度均为 *dₖ*。这会得出查询和键之间的相似性。接下来，相似性会根据模型隐藏维度的平方根进行缩放；这是为了防止由于后续应用 softmax 而导致反向传播过程中出现梯度消失的必要步骤。在对缩放后的相似性应用 softmax 后，我们得到注意力权重。最后，我们对注意力权重和值（V）进行矩阵乘法，值的维度为 *dᵥ*。此步骤的结果是传递序列的上下文向量。
import torch
import torch.nn as nn
import numpy as np
class ScaledDotProductAttention(nn.Module):
def __init__(self, dk, dropout=None) -> None:
super().__init__()
self.dk = dk
self.drop = nn.Dropout(dropout)
self.softmax = nn.Softmax(dim=-1)
def forward(self, q, k, v, mask=None):
# inputs are projected | shape: q - (batch_size, *n_head, q_len, dk) k - (batch_size, *n_head, k_len, dk) v - (batch_size, *n_head, k_len, dv)
# compute dot prod w/ q & k then scale | shape: similarities - (batch_size, *n_head, q_len, k_len)
similarities = torch.matmul(q, k.transpose(-2, -1)) / np.sqrt(self.dk)
# apply mask (if required)
if mask is not None:
mask = mask.unsqueeze(1) # for multi-head attention
similarities = similarities.masked_fill(mask == 0,-1e9)
# compute attention weights | shape: attention - (batch_size, *n_head, q_len, k_len)
attention = self.softmax(similarities)
# drop attention weights
attention = self.drop(attention)
# compute context given v | shape: context - (batch_size, *n_head, q_len, dv)
context = torch.matmul(attention, v)
return context, attention
注意：在我的实现中，我在注意力权重与值进行矩阵乘法之前，会使用一个 dropout 层来正则化注意力权重。
缩放点积注意力允许 Transformer 并行地评估给定序列中词元之间的重要性。这种并行能力被证明是此架构组件的一大优势，因为先前的架构一直受限于顺序处理。不知何故，《Attention Is All You Need》论文的作者找到了通过多头注意力从该组件中获取更多性能的方法。
多头注意力
多头注意力图多头注意力是一个子层，它通过将查询和键值对分割成多个注意力头，同时执行多个缩放点积注意力计算。在此实现中，查询和键（两者维度均为 *dₖ*）以及值（维度为 *dᵥ*）都将被投影 *h* 次，其中“h”表示注意力头的数量。查询和键值对的投影由三个可学习的权重矩阵创建：查询的 *Wq*、键的 *Wₖ* 和值的 *Wᵥ*。查询和键值对的投影允许 Transformer 在不同位置关注多个子空间。
一旦投影并分成注意力头，查询和键值对之间的缩放点积注意力将在每个头内同时计算。接下来，分割成多个头的所得上下文向量将被连接在一起，形成一个单一的上下文向量；该向量与模型的维度匹配。现在统一后，上下文向量将使用一个独特的、可学习的权重矩阵 *Wₒ* 进行投影。此操作的结果将输出查询和键值对的最终上下文向量。
为了简化其底层运作，多头注意力让 Transformer 能够从不同角度查看序列的不同部分，从而提高了注意力的有效性。
class MultiHeadAttention(nn.Module):
def __init__(self, dm, dk, dv, nhead, bias=False, dropout=None) -> None:
super().__init__()
if dm % nhead != 0:
raise ValueError("Embedding dimensions (dm) must be evenly divisble by number of heads (nhead)")
self.dm = dm
self.dk = dk
self.dv = dv
self.nhead = nhead
self.wq = nn.Linear(dm, dk * nhead, bias=bias)
self.wk = nn.Linear(dm, dk * nhead, bias=bias)
self.wv = nn.Linear(dm, dv * nhead, bias=bias)
self.wo = nn.Linear(dv * nhead, dm)
self.scaled_dot_prod_attn = ScaledDotProductAttention(dk, dropout=dropout)
def forward(self, q, k, v, mask=None):
# inshape: q - (batch_size, q_len, dm) k & v - (batch_size, k_len, dm)
batch_size, q_len, k_len = q.size(0), q.size(1), k.size(1)
# linear projections into heads | shape: q - (batch_size, nhead, q_len, dk) k - (batch_size, nhead, k_len, dk) v - (batch_size, nhead, k_len, dv)
q = self.wq(q).view(batch_size, q_len, self.nhead, self.dk).transpose(1, 2)
k = self.wk(k).view(batch_size, k_len, self.nhead, self.dk).transpose(1, 2)
v = self.wv(v).view(batch_size, k_len, self.nhead, self.dv).transpose(1, 2)
# get context & attn weights | shape: attention - (batch_size, nhead, q_len, k_len) context - (batch_size, nhead, q_len, dv)
context, attention = self.scaled_dot_prod_attn(q, k, v, mask=mask)
# concat heads | shape: context - (batch_size, q_len, dm)
context = context.transpose(1, 2).contiguous().view(batch_size, q_len, self.dm)
# project context vector | shape: context - (batch_size, q_len, dm)
context = self.wo(context)
return context, attention
注意：用于投影查询和键值对的可学习权重矩阵没有偏差（即 *bias = False*）。
填充掩码和无后续掩码
您可能已经注意到在我们的 PyTorch 实现中，掩码应用于计算缩放点积注意力。掩码对注意力机制至关重要，并扮演着两个特定用例的角色：
- 确保在计算注意力时忽略序列中填充的位置。
- 防止解码器在训练期间预测词语时获得不公平的优势。
忽略填充
为了并行和高效训练，序列被批量处理，批处理中的所有序列必须具有相同的序列长度。由于训练数据中并非所有序列都具有完全相同的长度，因此我们将序列填充到相同长度，使其能够批量处理。由于填充对序列没有上下文含义，因此我们忽略存在填充的嵌入值；这正是填充掩码将要执行的操作。
def generate_pad_mask(seq, pad_id):
# inshape: seq - (batch_size, seq_len)
# mark non-pad True & pad False
mask = (seq != pad_id).unsqueeze(-2)
# outshape: mask - (batch_size, 1, seq_len)
return mask
当掩码应用于缩放点积注意力时，被标记为 False 的填充位置将被填充为极大的负数（例如，-1,000,000,000）。一旦应用 softmax 以获得注意力权重，这些值将变得微不足道，以至于用于更新填充位置权重的梯度将可以忽略不计。简单来说，填充位置将被忽略，不会用于序列的上下文化。
无后续掩码
在训练阶段，无后续掩码是必要的，因为它们确保解码器不会关注序列的后续位置，而是关注它已经在序列中预测过的位置。简单来说，它确保解码器学习逐个（即一个接一个）从它已经在给定句子中预测过的词语中预测每个词语，而不是向前查看以预测同一句子中的词语。
这是通过创建一个 *l x l* 矩阵实现的，其中 *l* 是序列的长度。矩阵的行表示解码器可以在“时间步”关注的序列位置，列表示序列中词元的位置。标记为 True 的位置可以被关注，而标记为 False 的位置不能被关注。
import torch
def generate_nopeak_pad_mask(trg, pad_id):
# inshape: trg - (batch_size, trg_len)
# create pad mask (True = no pad False = pad) | shape: trg_mask - (batch_size, 1, trg_len)
trg_mask = generate_pad_mask(trg, pad_id)
# create subsequent mask | shape: trg_nopeak_mask - (1, trg_len, trg_len)
trg_len = trg.size(1)
trg_nopeak_mask = torch.triu(torch.ones((1, trg_len, trg_len)) == 1)
trg_nopeak_mask = trg_nopeak_mask.transpose(1, 2)
# combine pad & subsequent mask shape
trg_mask = trg_mask & trg_nopeak_mask
# outshape: trg_mask - (batch_size, trg_len, trg_len)
return trg_mask
由于填充规则仍然适用，无后续掩码会与相应的填充掩码结合（逻辑与运算），以保持填充位置为 False，无论解码器是否可以关注该位置。从那里，在应用 softmax 时遵循相同的原则，本质上否定了对解码器中后续和填充位置的注意力。
词元化序列的示例张量（填充词元 ID = 0）
示例张量的填充掩码
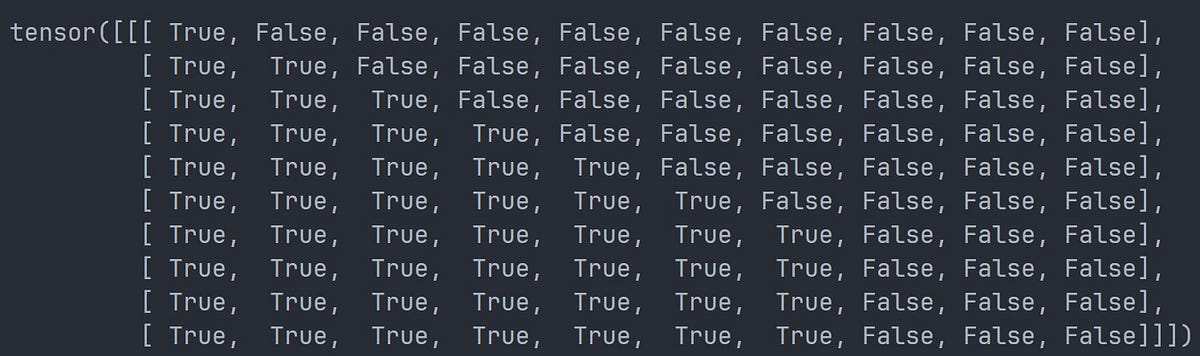示例张量的无后续掩码def generate_masks(src, trg, pad_id):
# inshape: src - (batch_size, src_len) trg - (batch_size, trg_len)
# create pad mask for src (True = no pad False = pad)
src_mask = generate_pad_mask(src, pad_id)
# generate pad nopeak mask for trg
trg_mask = generate_nopeak_pad_mask(trg, pad_id)
# outshape: src_mask - (batch_size, 1, src_len) trg_mask - (batch_size, trg_len, trg_len)
return src_mask, trg_mask
注意：此代码片段生成源序列和目标序列所需的掩码。
位置级前馈网络
大部分繁重的工作已经完成，我们可以探索位置级前馈网络。这个子层对于提升 Transformer 的学习能力至关重要。
位置级前馈网络函数前馈网络由两个可学习的权重矩阵 *W₁* 和 *W₂* 组成，它们之间有一个单一的 ReLU 激活函数。两个矩阵的维度由模型的隐藏维度和网络指定的维度定义。使用“Attention Is All You Need”论文中的参数，这些矩阵的维度分别为 *512x2048* 和 *2048x512*（即 *dff = 2048*）。
位置级前馈网络对于编码器和解码器块都至关重要，因为它对注意力模块进行参数化。如果没有它，传递给后续层中注意力模块的上下文向量只会“重新平均化”，从而阻碍模型的学习能力。因此，它的包含对于允许模型学习数据中复杂模式的更多功能是必要的（此处提供了更多关于其实现的解释）。
import torch.nn as nn
class FeedForwardNetwork(nn.Module):
def __init__(self, dm, dff, dropout=0.1) -> None:
super().__init__()
self.w1 = nn.Linear(dm, dff)
self.w2 = nn.Linear(dff, dm)
self.relu = nn.ReLU(inplace=False)
self.drop = nn.Dropout(dropout)
def forward(self, x):
# inshape: x - (batch_size, seq_len, dm)
# first linear transform with ReLU | shape: x - (batch_size, seq_len, dff)
x = self.relu(self.w1(x))
# drop neurons
x = self.drop(x)
# second linear transform | shape: out - (batch_size, seq_len, dm)
out = self.w2(x)
return out
注意：在我的实现中，我在第二次线性变换之前丢弃神经元，以帮助泛化并减少训练期间网络过拟合的可能性。
层归一化
层归一化公式，来自 PyTorch最后，但同样重要的是，我们有层归一化模块（LayerNorm）。层归一化是一种技术，用于根据输入的均值和方差对其特征进行归一化。在训练期间，层归一化模块使用 gamma (γ) 进行缩放，然后使用 beta (β) 移动特征的均值和方差。gamma 和 beta 都是可学习的参数，它们可能会随着模块试图稳定均值和方差而调整。在 Transformer 中，被归一化的特征是标记化序列的不同隐藏表示。
层归一化被整合到编码器和解码器块中，具有多种益处。首先，它在训练期间稳定梯度，从而提高学习性能。它还能加快收敛速度，从而全面减少训练时间。最后，它的存在可能会在推理期间引入更好的泛化能力（此处有一篇深入探讨层归一化的研究论文供进一步理解）。
import torch
import torch.nn as nn
class Norm(nn.Module):
def __init__(self, dm, eps=1e-6):
super().__init__()
self.gamma = nn.Parameter(torch.ones(dm))
self.beta = nn.Parameter(torch.zeros(dm))
self.eps = eps
def forward(self, x: torch.Tensor):
# inshape: x - (batch_size, seq_len, dm)
# calc mean & variance (along dm)
mean = x.mean(dim=-1, keepdim=True)
var = x.var(dim=-1, unbiased=True, keepdim=True)
# normalize, scale & shift | shape: out - (batch_size, seq_len, dm)
norm = (x - mean) / torch.sqrt(var + self.eps)
out = norm * self.gamma + self.beta
return out
描述了所有子层和模块后，我们可以创建编码器和解码器。
编码器块
编码器块在《Attention Is All You Need》论文中，编码器使用了多种组件才能有效运行。其主要组件是多头注意力和位置级前馈网络子层。除此之外，还使用 dropout、残差连接和层归一化来生成子层的最终输出。
残差连接
在 Transformer 中，所有子层的输出形状都与模型的维度（*dₘ = 512*）相同，这是为了实现残差连接。残差连接是 Transformer 编码器和解码器块中的一项关键技术。它们充当子层之间梯度的快捷方式，防止在反向传播过程中信息丢失。由于求和是线性运算，即使某些子层产生小梯度，通过残差连接的梯度在反向传播过程中也不会受到阻碍。残差连接还有助于使信息与子层的原始输入保持一致。在多头注意力中，输入被任意置换，这改变了它们的原始表示。残差连接基本上有助于子层“记住”它们的原始输入是什么。这确保了计算出的子层输出确实来自它们的原始输入，而不是来自置换后的修改（进一步解释）。
Dropout
Dropout 的工作原理是忽略一部分输入（即将其值设置为零），这意味着模型被迫独立学习输入的不同表示。这种正则化可以使模型不易过拟合，并提高其在推理时泛化到未见输入时的鲁棒性（您可以从这篇研究论文中了解更多关于 Dropout 的信息）。
子层输出
残差连接和 dropout 用于生成子层的最终输出。在传递到另一个子层之前，描述此输出的函数可以用以下伪代码定义：
output = LayerNorm(x + dropout(Sublayer(x)))
回到编码器块，输入序列（源）经过嵌入和位置编码。随后，结果被传递到多头注意力子层，在那里计算上下文向量。然后对上下文向量应用 Dropout，接着通过残差连接将其与多头注意力子层的原始输入相加。最后，将和进行归一化，并作为位置级前馈网络的新输入。
对于位置级前馈网络，重复相同的过程，只是输入是通过前馈网络而不是多头注意力子层。这生成了编码器块的最终输出，该输出稍后将用作解码器块中编码器-解码器注意力的输入。
import torch.nn as nn
from embedding import Embeddings
from pos_encoder import PositionalEncoder
from attention import MultiHeadAttention
from norm import Norm
from feedforward import FeedForwardNetwork
class EncoderLayer(nn.Module):
def __init__(self, dm, dk, dv, nhead, dff, bias=False, dropout=0.1, eps=1e-6) -> None:
super().__init__()
self.multihead = MultiHeadAttention(dm, dk, dv, nhead, bias=bias, dropout=dropout)
self.feedforward = FeedForwardNetwork(dm, dff, dropout=dropout)
self.norm1 = Norm(dm, eps=eps)
self.norm2 = Norm(dm, eps=eps)
self.drop1 = nn.Dropout(dropout)
self.drop2 = nn.Dropout(dropout)
def forward(self, src, src_mask=None):
# inshape: src - (batch_size, src_len, dm)
# get context | shape - x_out (batch_size, src_len, dm)
x = src
x_out, attn = self.multihead(x, x, x, mask=src_mask)
# drop neurons
x_out = self.drop1(x_out)
# add & norm (residual connections) | shape: x - (batch_size, src_len, dm)
x = self.norm1(x + x_out)
# linear transforms | shape: x_out (batch_size, src_len, dm)
x_out = self.feedforward(x)
# drop neurons
x_out = self.drop2(x_out)
# add & norm (residual connections) | shape: out - (batch_size, src_len, dm)
out = self.norm2(x + x_out)
return out, attn
class Encoder(nn.Module):
def __init__(self, vocab_size, maxlen, pad_id, dm, dk, dv, nhead, dff, layers=6, bias=False,
dropout=0.1, eps=1e-6, scale=True) -> None:
super().__init__()
self.embeddings = Embeddings(vocab_size, dm, pad_id)
self.pos_encodings = PositionalEncoder(dm, maxlen, dropout=dropout, scale=scale)
self.stack = nn.ModuleList([EncoderLayer(dm, dk, dv, nhead, dff, bias=bias, dropout=dropout, eps=eps)
for l in range(layers)])
def forward(self, src, src_mask=None):
# inshape: src - (batch_size, src_len, dm) src_mask - (batch_size, 1, src_len)
# embeddings + positional encodings | shape: x - (batch_size, src_len, dm)
x = self.embeddings(src)
x = self.pos_encodings(x)
# pass src through stack of encoders (out of layer is in for next)
for encoder in self.stack:
x, attn = encoder(x, src_mask=src_mask)
# shape: out - (batch_size, src_len, dm)
out = x
return out, attn
注意：编码器块可以多次堆叠，其中前一个块的输出是下一个块的输入。这些块的累积，或者更准确地说，它们的堆叠以及源嵌入和位置编码，构成了整个编码器。在“Attention Is All You Need”论文中，基础模型堆叠了六个（即 *N = 6*）。
解码器块
解码器块解码器块与编码器块非常相似，因为它嵌入并位置编码其输入，使用相同的子层输出方程（请参见“残差连接和 Dropout”部分），并使用位置级前馈网络作为其最终子层。然而，它采用掩码多头注意力，然后如前所述，采用编码器-解码器注意力。
掩码多头注意力类似于编码器块中的多头注意力。不同之处在于它应用了无后续掩码（参见“填充掩码和无后续掩码”部分），以防止解码器在学习生成输出序列（目标）时过早预测词元，或者“作弊”。
当计算掩码多头注意力时，上下文向量被传递到下一个多头注意力子层进行编码器-解码器注意力。在此实例中，由掩码多头注意力生成的上下文向量充当查询，而编码器的输出则用于键值对。此步骤教授模型如何将源序列“翻译”为目标序列。最后，从编码器-解码器注意力计算出的上下文向量通过位置级前馈网络，从而创建解码器块的最终输出。
import torch.nn as nn
from embedding import Embeddings
from pos_encoder import PositionalEncoder
from attention import MultiHeadAttention
from norm import Norm
from feedforward import FeedForwardNetwork
class DecoderLayer(nn.Module):
def __init__(self, dm, dk, dv, nhead, dff, bias=False, dropout=0.1, eps=1e-6) -> None:
super().__init__()
self.maskmultihead = MultiHeadAttention(dm, dk, dv, nhead, bias=bias, dropout=dropout)
self.multihead = MultiHeadAttention(dm, dk, dv, nhead, bias=bias, dropout=dropout)
self.feedforward = FeedForwardNetwork(dm, dff, dropout=dropout)
self.norm1 = Norm(dm, eps=eps)
self.norm2 = Norm(dm, eps=eps)
self.norm3 = Norm(dm, eps=eps)
self.drop1 = nn.Dropout(dropout)
self.drop2 = nn.Dropout(dropout)
self.drop3 = nn.Dropout(dropout)
def forward(self, src, trg, src_mask=None, trg_mask=None):
# inshape: src - (batch_size src_len, dm) trg - (batch_size, trg_len, dm) \
# src_mask - (batch_size, 1 src_len) trg_mask - (batch_size trg_len, trg_len)/(batch_size, 1 , trg_len)
# calc masked context | shape: x_out - (batch_size, trg_len, dm)
x = trg
x_out, attn1 = self.maskmultihead(x, x, x, mask=trg_mask)
# drop neurons
x_out = self.drop1(x_out)
# add & norm (residual connections) | shape: x - (batch_size, trg_len, dm)
x = self.norm1(x + x_out)
# calc context | shape: x_out - (batch_size, trg_len, dm)
x_out, attn2 = self.multihead(x, src, src, mask=src_mask)
# drop neurons
x_out = self.drop2(x_out)
# add & norm (residual connections) | shape: x - (batch_size, trg_len, dm)
x = self.norm2(x + x_out)
# calc linear transforms | shape: x_out - (batch_size, trg_len, dm)
x_out = self.feedforward(x)
# drop neurons
x_out = self.drop3(x_out)
# add & norm (residual connections) | shape: out - (batch_size, trg_len, dm)
out = self.norm3(x + x_out)
return out, attn1, attn2
class Decoder(nn.Module):
def __init__(self, vocab_size, maxlen, pad_id, dm, dk, dv, nhead, dff, layers=6, bias=False,
dropout=0.1, eps=1e-6, scale=True) -> None:
super().__init__()
self.embeddings = Embeddings(vocab_size, dm, pad_id)
self.pos_encodings = PositionalEncoder(dm, maxlen, dropout=dropout, scale=scale)
self.stack = nn.ModuleList([DecoderLayer(dm, dk, dv, nhead, dff, bias=bias, dropout=dropout, eps=eps)
for l in range(layers)])
def forward(self, src, trg, src_mask=None, trg_mask=None):
# inshape: src - (batch_size, src_len, dm) trg - (batch_size, trg_len, dm)
# embeddings + positional encodings | shape: x - (batch_size, trg_len, dm)
x = self.embeddings(trg)
x = self.pos_encodings(x)
# pass src & trg through stack of decoders (out of layer is in for next)
for decoder in self.stack:
x, attn1, attn2 = decoder(src, x, src_mask=src_mask, trg_mask=trg_mask)
out = x
return out, attn1, attn2
注意：与编码器块类似，解码器块也可以堆叠，并与目标嵌入和位置编码配对以形成整个解码器。原始论文使用了 *N = 6* 的堆叠。
现在，解码器输出实际上没什么可做的，因为它只是它的最终隐藏表示。由于我们的目标是生成一个向量，其中每个位置都包含目标词汇表中每个词的概率列表，因此隐藏表示被转换。
线性变换和 Softmax
线性变换和 softmax 应用线性变换
首先，解码器输出需要从模型的连续向量空间（维度）转换为目标词汇表的表示。这可以通过添加一个可学习的线性层来实现，该层的维度是模型的维度和目标词汇表中词元的数量（即 *dₘ* x *Vₜ*，其中 *Vₜ* 是目标词汇表中词元的数量）。
Softmax
下一步是为序列中的每个位置在目标词汇表上创建概率分布。这通过在目标词汇表的维度上对变换后的向量进行 softmax 计算，即可轻松实现。一旦应用，它将生成一个序列，其中每个位置对应于目标词汇表中每个词的概率列表，即预测的输出词元概率。
将所有部分组合在一起
在讨论了隐藏的细节和复杂性之后，我们终于可以开始将每一块拼图组合起来，构建一个 Transformer。
import torch.nn as nn
from encoder import Encoder
from decoder import Decoder
class Transformer(nn.Module):
def __init__(self, vocab_enc, vocab_dec, maxlen, pad_id, dm=512, dk=64, dv=64, nhead=8, layers=6,
dff=2048, bias=False, dropout=0.1, eps=1e-6, scale=True) -> None:
super().__init__()
self.encoder = Encoder(vocab_enc, maxlen, pad_id, dm, dk, dv, nhead, dff,
layers=layers, bias=bias, dropout=dropout, eps=eps, scale=scale)
self.decoder = Decoder(vocab_dec, maxlen, pad_id, dm, dk, dv, nhead, dff,
layers=layers, bias=bias, dropout=dropout, eps=eps, scale=scale)
self.linear = nn.Linear(dm, vocab_dec)
self.maxlen = maxlen
self.pad_id = pad_id
self.apply(xavier_init)
def forward(self, src, trg, src_mask=None, trg_mask=None):
# inshape: src - (batch_size, src_len) trg - (batch_size, trg_len)\
# src_mask - (batch_size, 1, src_len) trg_mask - (batch_size, 1, trg_len, trg_len)
# encode embeddings | shape: e_out - (batch_size, src_len, dm)
e_out, attn = self.encoder(src, src_mask=src_mask)
# decode embeddings | shape: d_out - (batch_size, trg_len, dm)
d_out, attn, attn = self.decoder(e_out, trg, src_mask=src_mask, trg_mask=trg_mask)
# linear transform decoder output | shape: out - (batch_size, trg_len, vocab_size)
out = self.linear(d_out)
return out
def xavier_init(module):
if hasattr(module, "weight") and module.weight.dim() > 1:
init.xavier_uniform_(module.weight.data)
注意：我想指出，在我们的代码中，解码器输出经过转换后没有应用 softmax。原因是在 PyTorch 中，用于训练 Transformer 的损失函数——交叉熵损失——在计算损失时会为您应用 softmax。此外，还使用了 Xavier 权重初始化来防止梯度消失和爆炸，并为模型在训练期间收敛提供一个良好的起点（关于权重初始化的更多直观理解可以在这篇文章中找到）。
训练
除非我们在一些数据上训练 Transformer 来进行翻译，否则我们无法真正利用它。下面是一个通用的训练函数，它使用自定义的 Pytorch DataLoader、Optimizer，并可选地使用所需设备（例如用于并行 GPU 计算的“cuda”），在一定数量的 epoch 中训练您的 Transformer。
import numpy as np
import torch.nn as nn
from utils.functional import generate_masks
def train(dataloader, model, optimizer, epochs=1000, device=None):
# setup
model.train()
m = len(dataloader)
cross_entropy = nn.CrossEntropyLoss(ignore_index=model.pad_id)
losses = []
# train over epochs
print("Training Started")
for epoch in range(epochs):
accum_loss = 0 # reset accumulative loss
for inputs, labels in dataloader:
# get src & trg
src, trg, out = inputs, labels[:, :-1], labels[:, 1:] # shape: src - (batch_size, src_len) trg & out - (batch_size, trg_len)
src, trg, out = src.long(), trg.long(), out.long()
# generate the masks
src_mask, trg_mask = generate_masks(src, trg, model.pad_id)
# move to device
src, trg, out = src.to(device), trg.to(device), out.to(device)
src_mask, trg_mask = src_mask.to(device), trg_mask.to(device)
# zero the grad
optimizer.zero_grad()
# get pred & reshape outputs
pred = model(src, trg, src_mask=src_mask, trg_mask=trg_mask) # shape: pred - (batch_size, seq_len, vocab_size)
pred, out = pred.contiguous().view(-1, pred.size(-1)), out.contiguous().view(-1) # shape: pred - (batch_size * seq_len, vocab_size) out - (batch_size * seq_len)
# calc grad & update model params
loss = cross_entropy(pred, out)
loss.backward()
optimizer.step()
# accumulate loss over time
accum_loss += loss.item()
# get epoch loss & keep track
epoch_loss = accum_loss / m
losses.append(epoch_loss)
print(f"Epoch {epoch + 1} Complete | Loss: {epoch_loss:.4f}")
# calc avg train loss
loss = np.mean(losses).item()
print(f"Training Complete | Average Loss: {loss:.4f}")
return loss
实验
在我的实验中，我训练 Transformer 进行英德语言翻译。我使用来自 torchtext 0.4.0 版本的 Multi30k 数据集训练和评估了该模型。对于配置和超参数，我复制了“Attention Is All You Need”论文中基础模型的设置。我采用了相同的 Adam 优化器，初始学习率为 0.00001（即 *lr = 1e-5*），*beta₁ = 0.9* 和 *beta₂ = 0.98*。我还包含了一个 调度器，如果测试损失在 10 个 epoch 内保持平稳，它会将学习率降低 10%。最后，我使用束搜索（beam search）和束宽 3 在推理期间解码词元。
我还使用了许多其他模块、工具和超参数，以帮助模型在训练过程中并查看其性能。如果您感兴趣，可以在我的 GitHub 仓库中找到我的完整实现。
结果
在 Lambda Cloud 的 Nvidia A10 GPU 上训练模型 1000 个 epoch 后，与原始“Attention Is All You Need”论文中的基础 Transformer 相比，我获得了卓越的性能。
Transformer 模型训练片段对于我的模型，在 Multi30k 数据集上的平均训练损失为 1.2493，平均测试损失为 2.5804，最佳 BLEU（双语评估替补）得分为 25.7。这个结果与“Attention Is All You Need”论文中对类似任务评估的 Transformer 结果（具体为 25.8）相比，差了 0.1。
Transformer 训练后的度量性能（红色为训练损失，蓝色为测试损失）结论
我们不仅一步步地剖析了 Transformer 模型，还使用 PyTorch 构建了一个，并且成功地训练了该模型，在英德翻译数据集上取得了令人满意的性能。
走到这一步，我希望我已经能够帮助您理解 Transformer 的复杂性，同时阐明其使其成为构建大型语言模型（LLM）的可行架构的特点。这项工作完成后，我要感谢您阅读本文，未来的工作，我计划深入研究仅解码器 Transformer 模型，其中最著名的是 ChatGPT。
敬请期待…