理解 BigBird 的块稀疏注意力机制
简介
基于 Transformer 的模型已被证明在许多 NLP 任务中非常有用。然而,基于 Transformer 的模型的一个主要限制是其 的时间和内存复杂度(其中 是序列长度)。因此,将基于 Transformer 的模型应用于长序列()在计算上非常昂贵。最近的一些论文,例如 Longformer、Performer、Reformer、Clustered attention 试图通过近似完整的注意力矩阵来解决这个问题。如果你不熟悉这些模型,可以查看 🤗 最近的这篇博文 post。
BigBird(在这篇论文中提出)是解决此问题的最新模型之一。BigBird 依赖于**块稀疏注意力**(block sparse attention)而不是普通的注意力(即 BERT 的注意力),并且可以处理长达 **4096** 的序列,其计算成本远低于 BERT。它在涉及非常长序列的各种任务上取得了 SOTA(State-of-the-Art)的成绩,例如长文档摘要、长上下文问答。
类 BigBird RoBERTa 的模型现已在 🤗Transformers 中提供。这篇文章的目标是让读者**深入**理解 BigBird 的实现,并简化在 🤗Transformers 中使用 BigBird 的过程。但在深入探讨之前,重要的是要记住,BigBird 的注意力是对 BERT 完整注意力的一种近似,因此它并不追求**优于** BERT 的完整注意力,而是为了更高效。它只是使得基于 Transformer 的模型能够应用于更长的序列,因为 BERT 的二次方内存需求很快变得无法承受。简而言之,如果我们拥有的计算资源和的时间,BERT 的注意力会比块稀疏注意力(我们将在本文中讨论)更受青睐。
如果你想知道为什么在处理更长序列时需要更多的计算资源,那么这篇博文正适合你!
在使用标准的类 BERT 注意力时,人们可能会有的一些主要问题包括:
- 所有的 token 真的都需要关注所有其他的 token 吗?
- 为什么不只计算对重要 token 的注意力呢?
- 如何判断哪些 token 是重要的?
- 如何以一种非常高效的方式只关注少数 token?
在这篇博文中,我们将尝试回答这些问题。
哪些 token 应该被关注?
我们将通过一个实际例子来解释注意力机制的工作原理,以句子 "BigBird is now available in HuggingFace for extractive question answering" 为例。在类 BERT 的注意力机制中,每个词都会简单地关注所有其他 token。用数学语言来说,这意味着每个查询 token ,都会关注完整的键 token 列表 。
让我们通过编写一些伪代码来思考一下,对于一个查询 token,哪些键 token 才是它真正应该关注的。我们将假设查询的 token 是 `available`,并为其构建一个合理的键 token 列表。
>>> # let's consider following sentence as an example
>>> example = ['BigBird', 'is', 'now', 'available', 'in', 'HuggingFace', 'for', 'extractive', 'question', 'answering']
>>> # further let's assume, we're trying to understand the representation of 'available' i.e.
>>> query_token = 'available'
>>> # We will initialize an empty `set` and fill up the tokens of our interest as we proceed in this section.
>>> key_tokens = [] # => currently 'available' token doesn't have anything to attend
邻近的 token 应该是重要的,因为在一个句子(词序列)中,当前词高度依赖于其相邻的过去和未来 token。这种直觉是 `滑动注意力`(sliding attention)概念背后的思想。
>>> # considering `window_size = 3`, we will consider 1 token to left & 1 to right of 'available'
>>> # left token: 'now' ; right token: 'in'
>>> sliding_tokens = ["now", "available", "in"]
>>> # let's update our collection with the above tokens
>>> key_tokens.append(sliding_tokens)
长程依赖:对于某些任务来说,捕捉 token 之间的长程关系至关重要。例如,在“问答”任务中,模型需要将上下文的每个 token 与整个问题进行比较,以便找出上下文的哪一部分对正确答案有用。如果大部分上下文 token 只关注其他上下文 token,而不关注问题,那么模型就很难从不太重要的上下文 token 中筛选出重要的上下文 token。
现在,`BigBird` 提出了两种在保持计算效率的同时允许长程注意力依赖的方法。
- 全局 token:引入一些 token,它们将关注每一个 token,并且被每一个 token 所关注。例如:“HuggingFace is building nice libraries for easy NLP”。现在,假设我们将“building”定义为一个全局 token,而模型需要知道“NLP”和“HuggingFace”之间的关系以完成某个任务(注意:这两个 token 位于句子的两端);现在让“building”全局关注所有其他 token,这很可能会帮助模型将“NLP”与“HuggingFace”联系起来。
>>> # let's assume 1st & last token to be `global`, then
>>> global_tokens = ["BigBird", "answering"]
>>> # fill up global tokens in our key tokens collection
>>> key_tokens.append(global_tokens)
- 随机 token:随机选择一些 token,它们通过将信息传递给其他 token,而这些 token 又可以将信息传递给其他 token,从而实现信息传递。这可以降低信息从一个 token 传递到另一个 token 的成本。
>>> # now we can choose `r` token randomly from our example sentence
>>> # let's choose 'is' assuming `r=1`
>>> random_tokens = ["is"] # Note: it is chosen compleletly randomly; so it can be anything else also.
>>> # fill random tokens to our collection
>>> key_tokens.append(random_tokens)
>>> # it's time to see what tokens are in our `key_tokens` list
>>> key_tokens
{'now', 'is', 'in', 'answering', 'available', 'BigBird'}
# Now, 'available' (query we choose in our 1st step) will attend only these tokens instead of attending the complete sequence
这样,查询 token 只关注所有可能 token 的一个子集,同时可以很好地近似完整的注意力。同样的方法也适用于所有其他查询 token。但请记住,这里的关键在于尽可能高效地近似 `BERT` 的完整注意力。简单地让每个查询 token 像 BERT 那样关注所有键 token,可以在现代硬件(如 GPU)上非常高效地计算为一系列矩阵乘法。然而,滑动、全局和随机注意力的组合似乎意味着稀疏矩阵乘法,这在现代硬件上难以高效实现。`BigBird` 的主要贡献之一是提出了一种 `块稀疏` 注意力机制,该机制可以有效地计算滑动、全局和随机注意力。让我们深入了解一下!
通过图理解全局、滑动和随机键的必要性
首先,让我们使用图来更好地理解 `全局`、`滑动` 和 `随机` 注意力,并尝试理解这三种注意力机制的组合如何能很好地近似标准的 `Bert-like` 注意力。
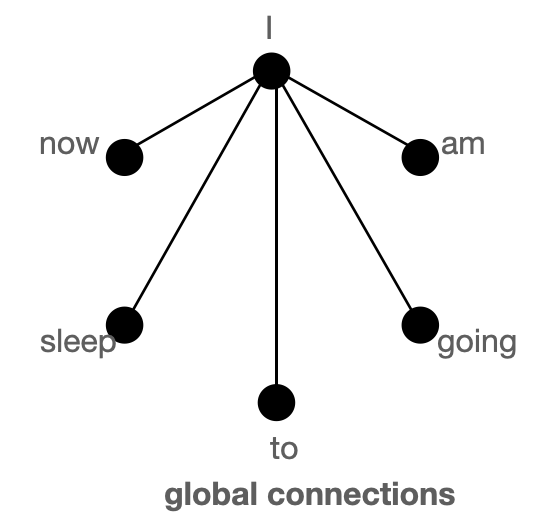
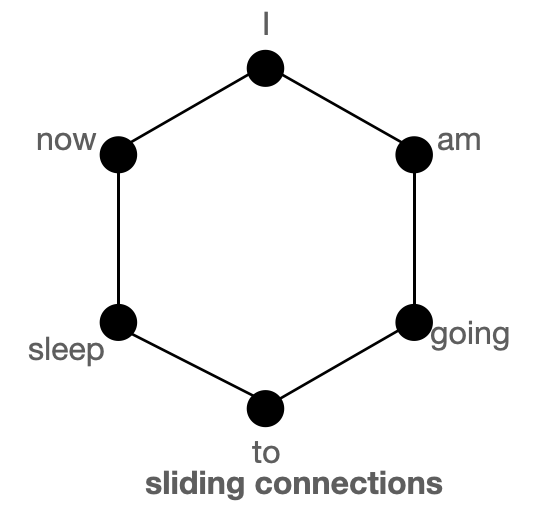
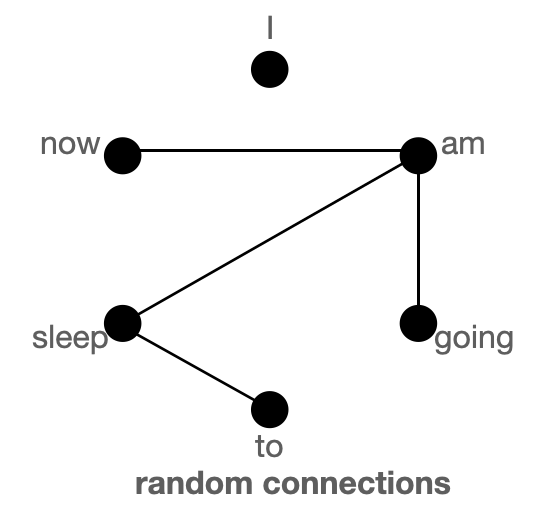
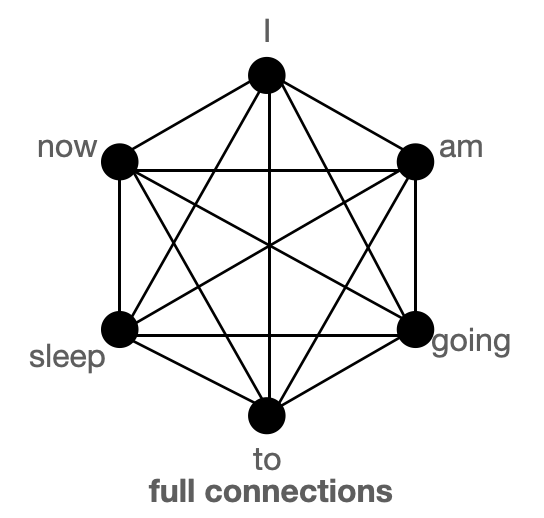
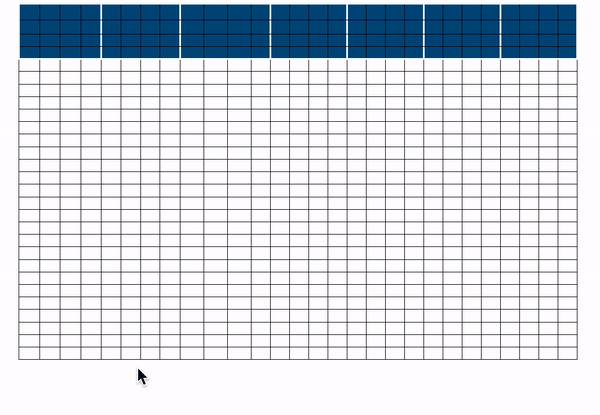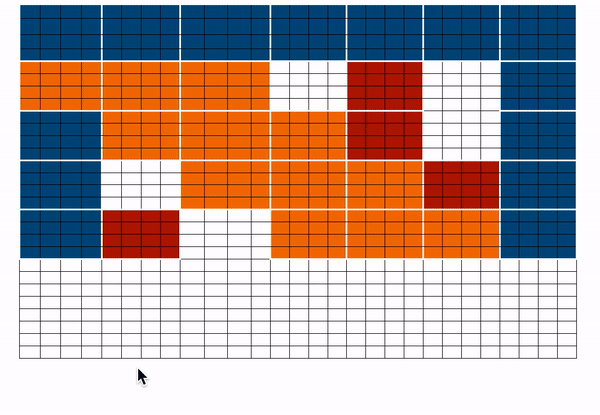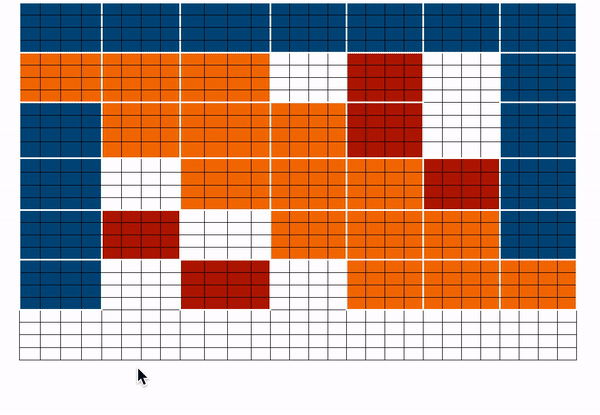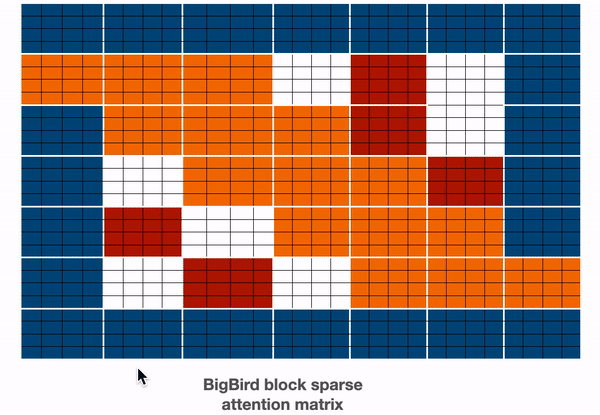
上图分别以图的形式展示了 `全局`(左)、`滑动`(中)和 `随机`(右)连接。每个节点对应一个 token,每条线代表一个注意力分数。如果两个 token 之间没有连接,则假定注意力分数为 0。
BigBird 块稀疏注意力是滑动、全局和随机连接的组合(总共 10 个连接),如左侧的 `gif` 所示。而一个**普通注意力**(右)的图将拥有所有 15 个连接(注意:总共有 6 个节点)。你可以简单地认为普通注意力是所有 token 都进行全局关注。
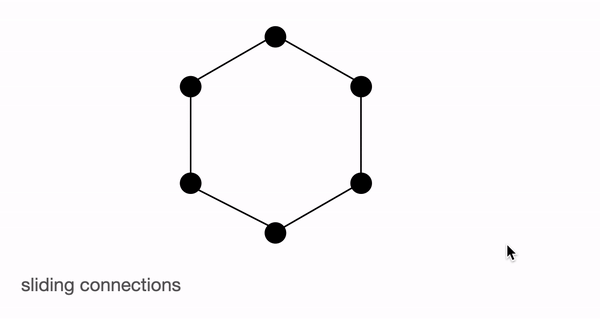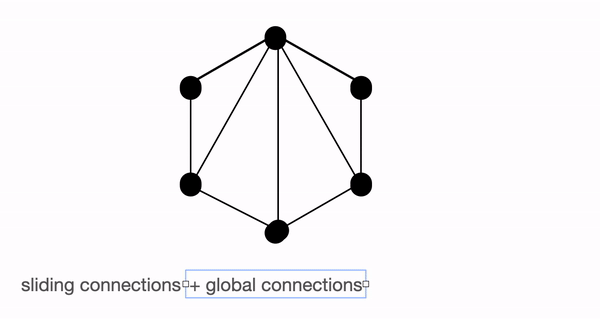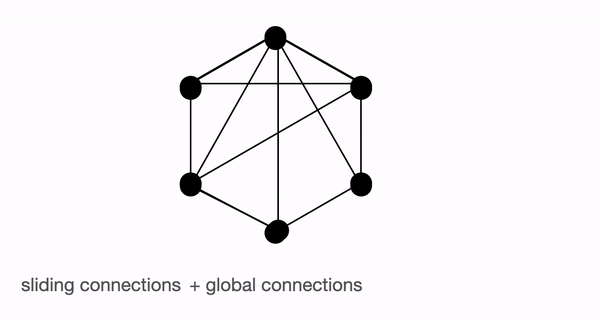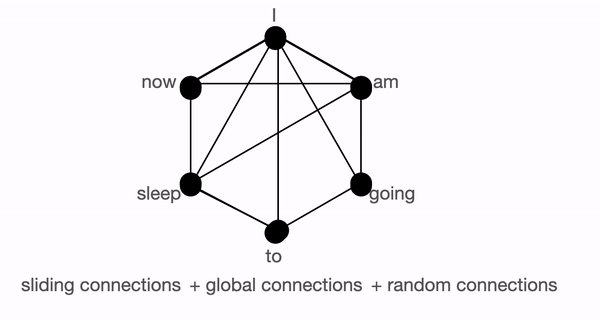
普通注意力:模型可以在单层内直接将信息从一个 token 传递到另一个 token,因为每个 token 都会查询所有其他 token,并被所有其他 token 关注。让我们考虑一个与上图类似的例子。如果模型需要将“going”与“now”关联起来,它可以在单层内简单地做到这一点,因为有一条直接连接这两个 token 的线。
块稀疏注意力:如果模型需要在两个节点(或 token)之间共享信息,对于某些 token,信息将不得不沿着路径上的其他各个节点传播;因为并非所有节点都在单层内直接连接。例如,假设模型需要将“going”与“now”关联起来,那么如果只有滑动注意力存在,这两个 token 之间的信息流将由路径:`going -> am -> i -> now` 定义(即信息必须经过另外两个 token)。因此,我们可能需要多层来捕捉序列的全部信息。而普通注意力可以在单层内捕捉到这一点。在极端情况下,这可能意味着需要与输入 token 数量一样多的层。然而,如果我们引入一些全局 token,信息可以通过路径:`going -> i -> now`(更短)传播。如果我们再引入随机连接,信息可以通过:`going -> am -> now` 传播。借助随机连接和全局连接,信息可以非常迅速地(只需几层)从一个 token 传递到下一个 token。
如果我们有很多全局 token,那么我们可能就不需要随机连接了,因为将会有多条短路径可以供信息传播。这就是在处理 BigBird 的一个变体 ETC(稍后会详细介绍)时,将 `num_random_tokens = 0` 的原因。
在这些图形中,我们假设注意力矩阵是对称的,**即** ,因为在图中如果某个 token **A** 关注 **B**,那么 **B** 也会关注 **A**。从下一节展示的注意力矩阵图中可以看出,这个假设对于 BigBird 中的大多数 token 是成立的。
| 注意力类型 | 全局 token |
滑动 token |
随机 token |
|---|---|---|---|
原始完整注意力 |
n |
0 | 0 |
块稀疏注意力 |
2 x block_size |
3 x block_size |
num_random_blocks x block_size |
original_full 代表 `BERT` 的注意力,而 `block_sparse` 代表 `BigBird` 的注意力。想知道 `block_size` 是什么吗?我们将在后面的章节中介绍。现在,为简单起见,可以将其视为 1。
BigBird 块稀疏注意力
BigBird 块稀疏注意力只是我们上面讨论内容的一种高效实现。每个 token 只关注一些**全局 token**、**滑动 token** 和**随机 token**,而不是关注**所有**其他 token。作者为多个查询组件分别硬编码了注意力矩阵,并使用了一个巧妙的技巧来加速在 GPU 和 TPU 上的训练/推理。
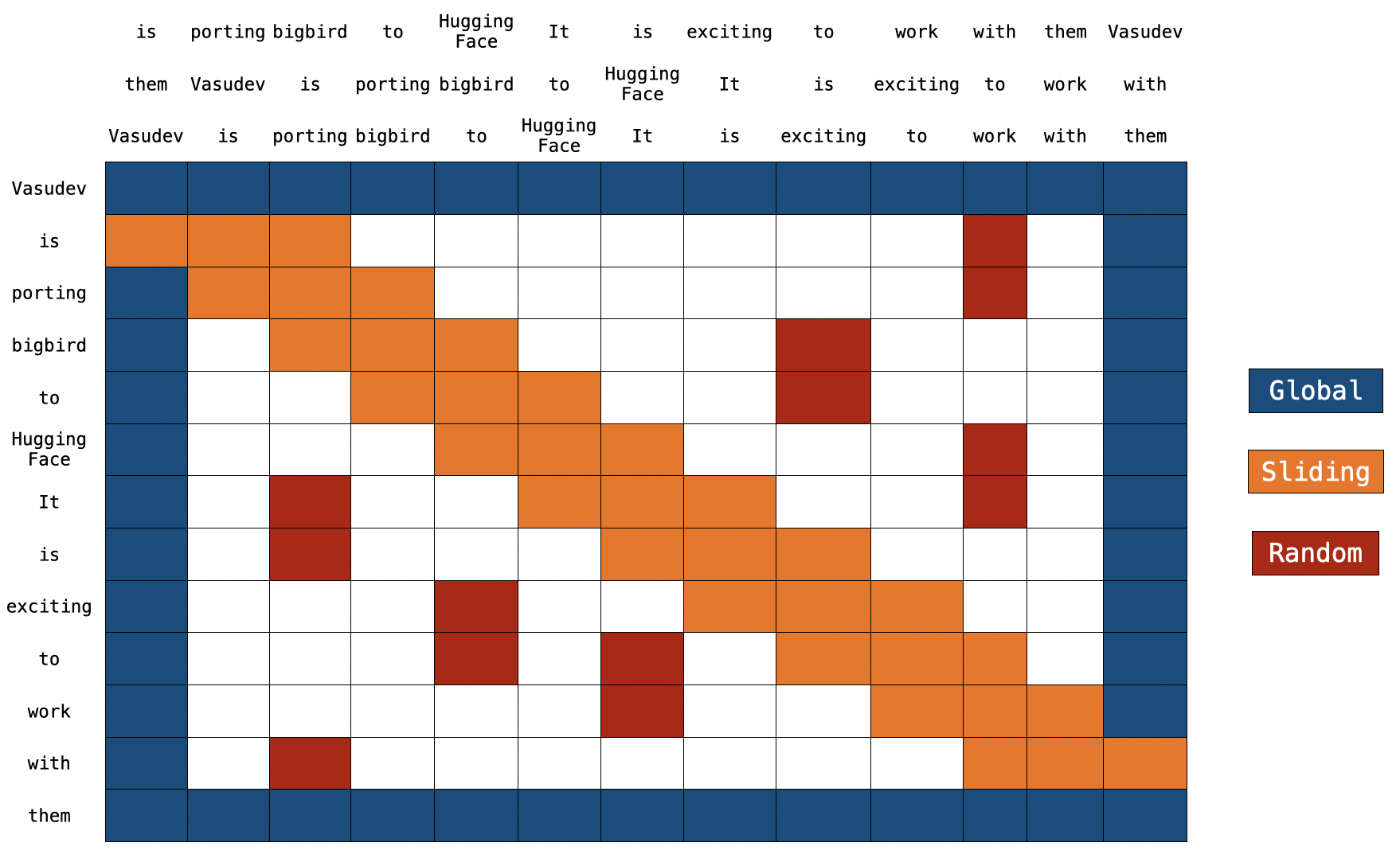 注意:在顶部,我们有两个额外的句子。正如你所注意到的,在两个句子中,每个 token 都只移动了一个位置。这就是滑动注意力的实现方式。当 `q[i]` 与 `k[i,0:3]` 相乘时,我们将得到 `q[i]` 的滑动注意力分数(其中 `i` 是序列中元素的索引)。
注意:在顶部,我们有两个额外的句子。正如你所注意到的,在两个句子中,每个 token 都只移动了一个位置。这就是滑动注意力的实现方式。当 `q[i]` 与 `k[i,0:3]` 相乘时,我们将得到 `q[i]` 的滑动注意力分数(其中 `i` 是序列中元素的索引)。
你可以在这里找到 `block_sparse` 注意力的实际实现。现在看起来可能很吓人😨😨。但这篇文章肯定会让你更容易理解这段代码。
全局注意力
对于全局注意力,每个查询都简单地关注序列中的所有其他 token,并被所有其他 token 关注。让我们假设 `Vasudev`(第一个 token)和 `them`(最后一个 token)是全局的(如上图所示)。你可以看到这些 token 直接连接到所有其他 token(蓝色方框)。
# pseudo code
Q -> Query martix (seq_length, head_dim)
K -> Key matrix (seq_length, head_dim)
# 1st & last token attends all other tokens
Q[0] x [K[0], K[1], K[2], ......, K[n-1]]
Q[n-1] x [K[0], K[1], K[2], ......, K[n-1]]
# 1st & last token getting attended by all other tokens
K[0] x [Q[0], Q[1], Q[2], ......, Q[n-1]]
K[n-1] x [Q[0], Q[1], Q[2], ......, Q[n-1]]
滑动注意力
将键 token 序列复制 2 次,其中一个副本中的每个元素向右移动,另一个副本中的每个元素向左移动。现在,如果我们将查询序列向量与这 3 个序列向量相乘,我们就能覆盖所有的滑动 token。计算复杂度仅为 `O(3xn) = O(n)`。参考上图,橙色方框代表滑动注意力。你可以在图的顶部看到 3 个序列,其中 2 个被移动了一个 token(一个向左,一个向右)。
# what we want to do
Q[i] x [K[i-1], K[i], K[i+1]] for i = 1:-1
# efficient implementation in code (assume dot product multiplication 👇)
[Q[0], Q[1], Q[2], ......, Q[n-2], Q[n-1]] x [K[1], K[2], K[3], ......, K[n-1], K[0]]
[Q[0], Q[1], Q[2], ......, Q[n-1]] x [K[n-1], K[0], K[1], ......, K[n-2]]
[Q[0], Q[1], Q[2], ......, Q[n-1]] x [K[0], K[1], K[2], ......, K[n-1]]
# Each sequence is getting multiplied by only 3 sequences to keep `window_size = 3`.
# Some computations might be missing; this is just a rough idea.
随机注意力
随机注意力确保每个查询 token 也会关注一些随机的 token。对于实际实现来说,这意味着模型会随机收集一些 token 并计算它们的注意力分数。
# r1, r2, r are some random indices; Note: r1, r2, r3 are different for each row 👇
Q[1] x [K[r1], K[r2], ......, K[r]]
.
.
.
Q[n-2] x [K[r1], K[r2], ......, K[r]]
# leaving 0th & (n-1)th token since they are already global
注意:当前的实现进一步将序列划分为块(block),每个符号都是相对于块而不是 token 来定义的。我们将在下一节更详细地讨论这一点。
实现
回顾:在常规的 BERT 注意力机制中,一个 token 序列,即 ,通过一个全连接层投影成 ,注意力分数 的计算公式为 。在 BigBird 块稀疏注意力中,使用的是相同的算法,但只使用部分选定的查询和键向量。
让我们来看看 bigbird 块稀疏注意力是如何实现的。首先,我们假设 分别代表 `block_size`(块大小)、`num_random_blocks`(随机块数)、`num_sliding_blocks`(滑动块数)、`num_global_blocks`(全局块数)。在视觉上,我们可以用 来说明 big bird 块稀疏注意力的组成部分,如下所示:
的注意力分数是分别计算的,如下所述:
由 表示的 的注意力分数,其中 ,这其实就是第一个块中的所有 token 与序列中所有其他 token 之间的注意力分数。
 代表第一个块, 代表第 个块。我们只是在 和 (即所有的键)之间执行普通的注意力操作。
代表第一个块, 代表第 个块。我们只是在 和 (即所有的键)之间执行普通的注意力操作。
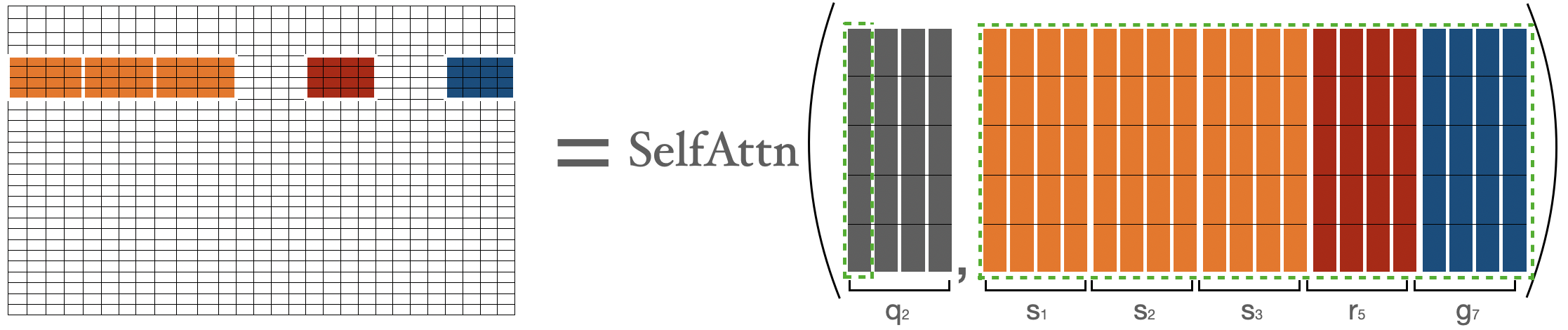
为了计算第二个块中 token 的注意力分数,我们收集前三个块、最后一个块和第五个块。然后我们可以计算 。
我用 来表示 token,只是为了明确地表示它们的性质(即显示全局、随机、滑动 token),否则它们都只是 。
为了计算 的注意力分数,我们将收集全局、滑动、随机键,并对 和收集到的键执行普通的注意力操作。请注意,滑动键是使用前面在滑动注意力部分讨论过的特殊移动技巧收集的。
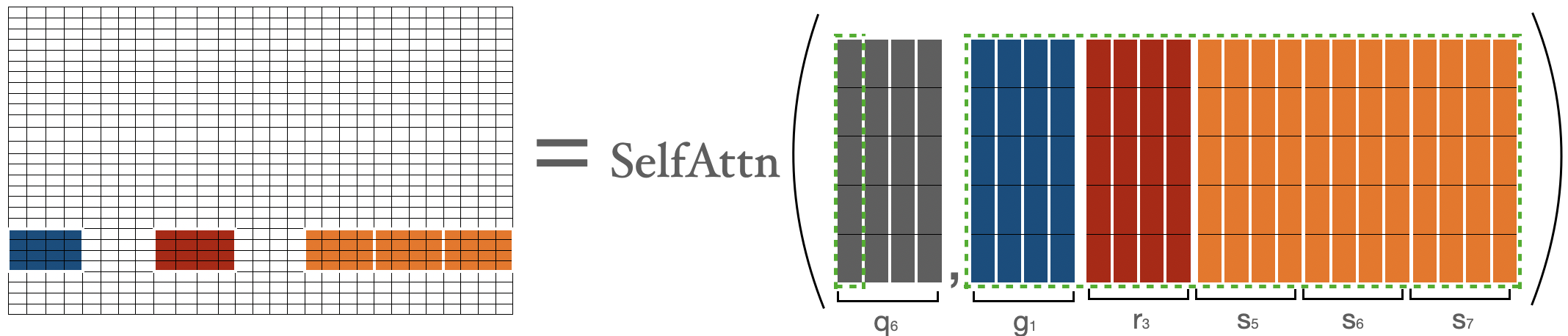
为了计算倒数第二个块中 token 的注意力分数(即 ),我们收集第一个块、最后三个块和第三个块。然后我们可以应用公式 。这与我们对 所做的非常相似。
的注意力分数由 表示,其中 ,这其实就是最后一个块中的所有 token 与序列中所有其他 token 之间的注意力分数。这与我们对 所做的非常相似。
让我们结合上述矩阵来得到最终的注意力矩阵。这个注意力矩阵可以用来获得所有 token 的表示。
`蓝色 -> 全局块`,`红色 -> 随机块`,`橙色 -> 滑动块`。这个注意力矩阵仅用于说明。在前向传播过程中,我们不会存储 `白色` 块,而是如上所述,直接为每个分离的组件计算一个加权值矩阵(即每个 token 的表示)。
现在,我们已经介绍了块稀疏注意力最难的部分,即其实现。希望你现在对理解实际代码有了更好的背景知识。欢迎深入研究代码,并将代码的每个部分与上述组件之一联系起来。
时间与内存复杂度
| 注意力类型 | 序列长度 | 时间与内存复杂度 |
|---|---|---|
原始完整注意力 |
512 | T |
| 1024 | 4 x `T` | |
| 4096 | 64 x `T` | |
块稀疏注意力 |
1024 | 2 x `T` |
| 4096 | 8 x `T` |
BERT 注意力与 BigBird 块稀疏注意力的时间与空间复杂度比较。
展开此代码段以查看计算过程
BigBird time complexity = O(w x n + r x n + g x n)
BERT time complexity = O(n^2)
Assumptions:
w = 3 x 64
r = 3 x 64
g = 2 x 64
When seqlen = 512
=> **time complexity in BERT = 512^2**
When seqlen = 1024
=> time complexity in BERT = (2 x 512)^2
=> **time complexity in BERT = 4 x 512^2**
=> time complexity in BigBird = (8 x 64) x (2 x 512)
=> **time complexity in BigBird = 2 x 512^2**
When seqlen = 4096
=> time complexity in BERT = (8 x 512)^2
=> **time complexity in BERT = 64 x 512^2**
=> compute in BigBird = (8 x 64) x (8 x 512)
=> compute in BigBird = 8 x (512 x 512)
=> **time complexity in BigBird = 8 x 512^2**
ITC vs ETC
BigBird 模型可以使用两种不同的策略进行训练:**ITC** 和 **ETC**。ITC (internal transformer construction,内部 Transformer 构建) 就是我们上面讨论的内容。在 ETC (extended transformer construction,扩展 Transformer 构建) 中,一些额外的 token 被设为全局,这样它们将关注所有 token,并被所有 token 关注。
ITC 需要较少的计算资源,因为只有很少的 token 是全局的,同时模型仍能捕捉到足够的全局信息(也借助了随机注意力)。另一方面,ETC 对于那些需要大量全局 token 的任务非常有用,例如“问答”,其中整个问题应该被上下文全局关注,以便能够将上下文与问题正确关联起来。
注意:Big Bird 论文中表明,在许多 ETC 实验中,随机块的数量被设置为 0。根据我们在图部分的讨论,这是合理的。
下表总结了 ITC 和 ETC
| ITC | ETC | |
|---|---|---|
| 带全局注意力的注意力矩阵 | ||
全局 token |
2 x block_size |
extra_tokens + 2 x block_size |
随机 token |
num_random_blocks x block_size |
num_random_blocks x block_size |
滑动 token |
3 x block_size |
3 x block_size |
在 🤗Transformers 中使用 BigBird
你可以像使用其他 🤗 模型一样使用 BigBirdModel。下面我们来看一些代码示例。
from transformers import BigBirdModel
# loading bigbird from its pretrained checkpoint
model = BigBirdModel.from_pretrained("google/bigbird-roberta-base")
# This will init the model with default configuration i.e. attention_type = "block_sparse" num_random_blocks = 3, block_size = 64.
# But You can freely change these arguments with any checkpoint. These 3 arguments will just change the number of tokens each query token is going to attend.
model = BigBirdModel.from_pretrained("google/bigbird-roberta-base", num_random_blocks=2, block_size=16)
# By setting attention_type to `original_full`, BigBird will be relying on the full attention of n^2 complexity. This way BigBird is 99.9 % similar to BERT.
model = BigBirdModel.from_pretrained("google/bigbird-roberta-base", attention_type="original_full")
在撰写本文时,🤗Hub 中总共有 3 个检查点可用:bigbird-roberta-base、bigbird-roberta-large、bigbird-base-trivia-itc。前两个检查点来自使用 masked_lm loss 预训练 BigBirdForPretraining;而最后一个是在 trivia-qa 数据集上微调 BigBirdForQuestionAnswering 后的检查点。
让我们看一些你可以编写的最简代码(如果你喜欢使用自己的 PyTorch 训练器),以使用 🤗 的 BigBird 模型来微调你的任务。
# let's consider our task to be question-answering as an example
from transformers import BigBirdForQuestionAnswering, BigBirdTokenizer
import torch
device = torch.device("cpu")
if torch.cuda.is_available():
device = torch.device("cuda")
# lets initialize bigbird model from pretrained weights with randomly initialized head on its top
model = BigBirdForQuestionAnswering.from_pretrained("google/bigbird-roberta-base", block_size=64, num_random_blocks=3)
tokenizer = BigBirdTokenizer.from_pretrained("google/bigbird-roberta-base")
model.to(device)
dataset = "torch.utils.data.DataLoader object"
optimizer = "torch.optim object"
epochs = ...
# very minimal training loop
for e in range(epochs):
for batch in dataset:
model.train()
batch = {k: batch[k].to(device) for k in batch}
# forward pass
output = model(**batch)
# back-propogation
output["loss"].backward()
optimizer.step()
optimizer.zero_grad()
# let's save final weights in a local directory
model.save_pretrained("<YOUR-WEIGHTS-DIR>")
# let's push our weights to 🤗Hub
from huggingface_hub import ModelHubMixin
ModelHubMixin.push_to_hub("<YOUR-WEIGHTS-DIR>", model_id="<YOUR-FINETUNED-ID>")
# using finetuned model for inference
question = ["How are you doing?", "How is life going?"]
context = ["<some big context having ans-1>", "<some big context having ans-2>"]
batch = tokenizer(question, context, return_tensors="pt")
batch = {k: batch[k].to(device) for k in batch}
model = BigBirdForQuestionAnswering.from_pretrained("<YOUR-FINETUNED-ID>")
model.to(device)
with torch.no_grad():
start_logits, end_logits = model(**batch).to_tuple()
# now decode start_logits, end_logits with what ever strategy you want.
# Note:
# This was very minimal code (in case you want to use raw PyTorch) just for showing how BigBird can be used very easily
# I would suggest using 🤗Trainer to have access for a lot of features
在使用 BigBird 时,务必牢记以下几点:
- 序列长度必须是块大小的倍数,即
seqlen % block_size = 0。你无需担心,因为如果批次序列长度不是block_size的倍数,🤗Transformers 会自动进行<pad>(填充到大于序列长度的最小块大小倍数)。 - 目前,HuggingFace 版本不支持 ETC,因此只有第一个和最后一个块是全局的。
- 当前的实现不支持
num_random_blocks = 0。 - 作者建议在序列长度小于 1024 时设置
attention_type = "original_full"。 - 必须满足以下条件:
seq_length > global_token + random_tokens + sliding_tokens + buffer_tokens,其中global_tokens = 2 x block_size、sliding_tokens = 3 x block_size、random_tokens = num_random_blocks x block_size和buffer_tokens = num_random_blocks x block_size。如果你未能满足此条件,🤗Transformers 会自动将attention_type切换为original_full并显示一条警告。 - 当使用 BigBird 作为解码器(或使用
BigBirdForCasualLM)时,attention_type应该是original_full。但你无需担心,如果你忘记设置,🤗Transformers 会自动将attention_type切换为original_full。
下一步是什么?
@patrickvonplaten 制作了一个非常酷的 notebook,介绍了如何在 trivia-qa 数据集上评估 BigBirdForQuestionAnswering。欢迎使用该 notebook 来体验 BigBird。
你很快就会在库中找到类似 BigBird Pegasus 的模型,用于长文档摘要任务💥。