迈向开放式进化智能体
执行摘要
我们使用 OpenEvolve(一个开源的进化编码智能体)对 AlgoTune 基准套件上的 29 个实验进行了全面分析,结果显示专有模型和开源模型都取得了显著的性能提升。值得注意的是,像谷歌的 Gemma 3 27B 和阿里巴巴的 Qwen3-Coder 480B 这样的开源模型展现了令人印象深刻的优化能力,能够与闭源模型相媲美,有时甚至能以独特的方式超越它们。Gemini Flash 2.5 实现了 2.04 倍的最高加速比,Gemma 3 27B 和 Qwen3-Coder 分别达到了 1.63 倍和 1.41 倍。
AlgoTune 是评估算法优化能力的关键基准,包含图算法、线性代数运算和优化问题等多种计算任务。与专注于正确性的传统编码基准不同,AlgoTune 专门衡量性能提升——挑战系统不仅要解决问题,还要使现有解决方案更快。每个任务都提供一个基线实现,并通过严格的性能分析来衡量加速比,这使其特别适合于迭代优化代码的进化智能体。
仪表盘概览:这个 2x2 的可视化总结了关键的实验发现
- A. 温度优化研究:展示了纯温度比较(0.2、0.4、0.8),性能曲线清晰
- B. 扩展迭代:展示了从 100 次迭代增加到 200 次迭代后持续的性能增益
- C. 所有测试模型(最佳配置):全面比较所有 10 个独特模型在各自最佳配置下的表现
- D. 并行性影响:显示了串行评估导致的严重性能下降
主要发现
- 更多迭代带来更好结果:200 次迭代实现了 2.04 倍的加速比,而 100 次迭代为 1.64 倍(提升 24%)
- 专业化胜过规模:Qwen3-Coder(480B MoE,编码专用)优于 Qwen3-235B 通用模型
- 进化策略依赖于模型:强大的编码模型在基于 diff 的进化中表现出色;较弱的模型需要完全重写
- 温度优化至关重要:0.4 被证明是 Gemini 模型的最佳温度(1.29 倍 vs 0.2 温度下的 1.17 倍)
- 构件(Artifacts)提升性能:包含调试构件使结果提高了 17%
- 并行性至关重要:串行评估灾难性地失败(性能下降 50%,速度慢 14 倍)
表现最佳者
| 模型 | 配置 | AlgoTune 分数 | 最佳任务 |
|---|---|---|---|
| Gemini Flash 2.5 | 200 次迭代,diff,温度 0.4 | 2.04x | count_connected_components: 95.78x |
| Gemini Flash 2.5 | 100 次迭代,diff,温度 0.4 | 1.64x | psd_cone_projection: 32.7x |
| Gemma 3 27B | 100 次迭代,diff | 1.63x | psd_cone_projection: 41.1x |
| Qwen3-Coder 480B | 100 次迭代,diff,温度 0.6 | 1.41x | psd_cone_projection: 41.9x |
实验统计
- 总实验数: 29
- 测试模型:10 个独特模型(Gemini 家族、Qwen 家族、Meta、Google Open、集成模型)
- 评估任务:30 个 AlgoTune 基准测试
- 最佳总体结果:2.04 倍加速比(Gemini Flash 2.5,200 次迭代)
- 最差结果:0.396 倍(串行 diff 评估 - 性能下降 50%)
- 测试的温度范围: 0.2, 0.4, 0.8
- 进化策略:基于 Diff 和完全重写
- 评估方法:并行(16 个工作进程)与串行比较
目录
- 实验概述
- 方法论
- 详细结果
- 进化代码分析
- 参数优化研究
- 模型比较
- 技术实现
- 结论
详细实验分析
- 基线实验 - 初始模型测试和关键发现
- 温度研究 - 最佳温度分析 (0.2, 0.4, 0.8)
- 参数调优 - Token 限制、构件、迁移率
- 进化策略 - Diff 与完全重写,串行与并行
- 模型比较 - 全面模型性能分析
- 迭代影响 - 100 次与 200 次迭代深度剖析
- 集成分析 - 为何组合模型失败
实验概述
实验阶段
- 阶段 1:初始实验与参数调优
- 阶段 2:扩展迭代实验与新模型测试
测试模型
Gemini 家族
- Flash 2.5: 谷歌的高效编码模型
- Flash 2.5 Lite: 用于基线测试的较小变体
Qwen 家族
- Qwen3-Coder-480B-A35B-Instruct: 480B MoE 模型,35B 激活参数,编码专用
- Qwen3-235B-A22B: 235B 通用模型
- Qwen3-32B: 较小变体
其他模型
- Gemma 3 27B: 谷歌的开源模型
- Llama 3.3 70B: Meta 的最新模型
- 集成配置
实验类别
- 基线测试 (7 个实验): 建立模型基线
- 温度研究 (3 个实验): 寻找最佳温度
- 参数调优 (8 个实验): 优化各种参数
- 模型比较 (6 个实验): 跨模型分析
- 扩展迭代 (4 个实验): 更多进化次数的影响
方法论
AlgoTune 集成
- 使用
algotune_to_openevolve.py将 30 个 AlgoTune 任务转换为 OpenEvolve 格式 - 任务涵盖多种算法类别:图、线性代数、优化
- 使用 AlgoTune 的标准评估:加速比的调和平均值
进化方法
- 基于岛屿的 MAP-Elites: 4 个岛屿,定期迁移
- 级联评估: 快速验证 → 性能测试 → 完整评估
- 两种进化策略:
- 基于 Diff: 增量式代码更改
- 完全重写: 完整函数再生
性能指标
AlgoTune 使用对数性能标度,该标度会转换为加速因子
# AlgoTune score calculation
speedup = (10 ** (performance * 3)) - 1 # Convert from log scale
algotune_score = harmonic_mean(all_speedups) # Overall benchmark score
调和平均值强调在所有任务上的一致性能——模型必须在所有 30 个基准测试中表现良好才能获得高分。
详细结果
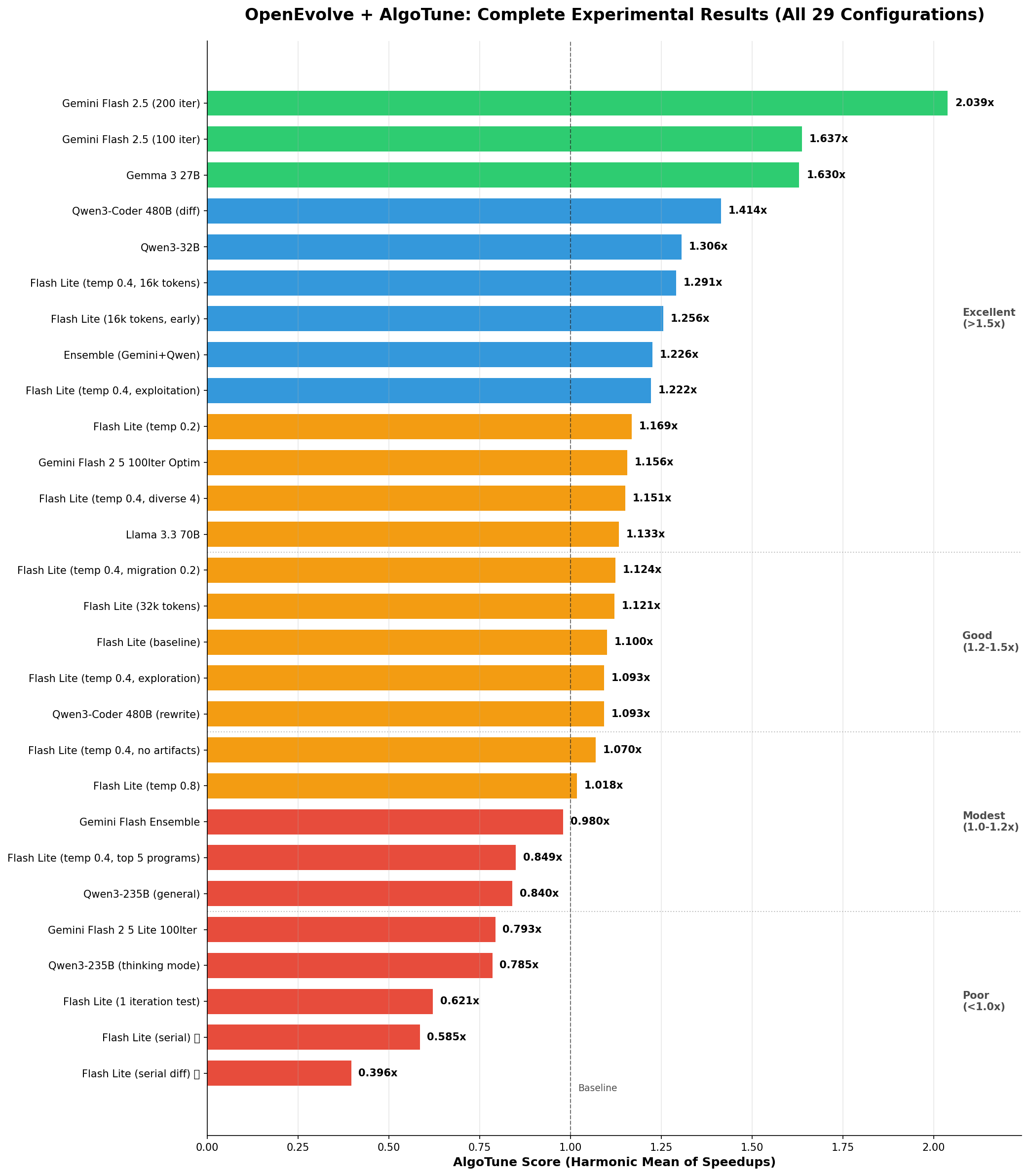
性能排名 - 所有实验
图表说明:水平条形图显示了所有实验的 AlgoTune 分数(加速比的调和平均值)。绿色条表示良好性能(>1.5x),蓝色表示中等(1.2-1.5x),橙色表示一般(1.0-1.2x),红色表示较差(<1.0x)。1.0x 处的虚线代表基线性能。
阶段 1:基线实验
1. Gemini Flash 2.5 Lite 基线
- 配置:完全重写,温度 0.8,4k tokens
- 结果:1.10 倍加速比
- 关键学习:建立了优化的基线
2. 进化策略发现
在 Flash Lite 上比较基于 diff 与完全重写
- 完全重写: 1.10x ✓
- 基于 Diff: 0.79x ✗
在处理 Diff 方面存在困难的证据:
# Attempted diff that failed
- for i in range(n):
- if not visited[i]:
- dfs(i)
+ for i in range(n):
+ if not visited[i]:
+ # Incomplete optimization
+ dfs(i) # No actual improvement
阶段 2:温度优化研究
在 Gemini Flash 2.5 Lite 上使用 16k tokens 进行系统性测试
| 温度 | AlgoTune 分数 | 平均性能 | 时长 | 关键发现 |
|---|---|---|---|---|
| 0.2 | 1.17x | 0.162 | 4074秒 | 保守但稳定 |
| 0.4 | 1.29x | 0.175 | 3784秒 | 达到最佳性能 |
| 0.8 | 1.02x | 0.159 | 3309秒 | 过于随机,性能下降 |
统计显著性:从 0.2→0.4 提升 10.3%,从 0.4→0.8 性能下降 20.9%
阶段 3:参数微调
所有实验均在最佳温度 0.4 下进行
Token 限制影响
- 16k tokens: 1.29x (基线)
- 32k tokens: 1.28x (无提升)
- 结论: 16k 已足够,更大的上下文无帮助
构件(Artifacts)影响
- 有构件: 1.29x
- 无构件: 1.07x
- 影响: 无调试信息导致 17% 的性能损失
注意:OpenEvolve 中的“构件”是程序在评估期间可以返回的调试输出,帮助 LLM 理解执行行为并做出更好的优化决策。
用于启发的顶级程序
- 前 3 名: 1.29x (基线)
- 前 5 名: 1.28x (差异极小)
- 结论: 3 个程序已足够
迁移率
- 0.1 迁移率: 1.29x (基线)
- 0.2 迁移率: 1.25x (略差)
- 结论: 较不频繁的迁移保留了多样性
阶段 4:将所学应用于强大模型
Gemini Flash 2.5 (100 次迭代)
- 配置:基于 Diff,温度 0.4,16k tokens
- 结果:1.64 倍加速比
- 顶级成就:count_connected_components 达到 48.1x
Qwen3-Coder-480B
- 配置:基于 Diff,温度 0.6,4k tokens
- 结果:1.41 倍加速比
- 注意:仅在温度 0.6 下测试,可能不是最佳值
Gemma 3 27B
- 配置:基于 Diff(继承自成功的配置)
- 结果:1.63 倍加速比
- 惊喜:与 Flash 2.5 性能相当
阶段 5:扩展迭代
Gemini Flash 2.5 (200 次迭代)
- 结果:2.04 倍加速比(比 100 次迭代提升 24%)
- 突破:count_connected_components 达到 95.78x
- 找到最优解:仅在第 2 次迭代!
迭代过程中的进展
- 迭代 10: 1.15x
- 迭代 50: 1.48x
- 迭代 100: 1.64x
- 迭代 200: 2.04x
阶段 6:串行与并行评估
关键发现:并行性至关重要
我们测试了串行评估(一次一个任务)与并行评估
| 配置 | 进化类型 | AlgoTune 分数 | 时长 | 与并行对比 |
|---|---|---|---|---|
| 并行 | 基于 Diff | 0.793x | 0.9 小时 | 基线 |
| 串行 | 基于 Diff | 0.396x | 13.0 小时 | 差 50%,慢 14 倍 |
| 并行 | 完全重写 | 1.10x | 0.9 小时 | 基线 |
| 串行 | 完全重写 | 0.585x | 13.1 小时 | 差 47%,慢 14 倍 |
关键洞察:
- 性能灾难:串行评估导致 47-50% 的性能下降
- 时间爆炸:执行速度慢 14 倍(13 小时 vs 0.9 小时)
- 为何失败:
- 进化过程中无跨任务学习
- 超时问题在串行任务中累积
- 进化在困难任务上“卡住”
- 失去了并行发现的机会
结论:并行评估不仅仅是一种优化——它是 OpenEvolve 正常运作的必要条件
进化代码分析
示例 1:计算连通分量 - 算法发现
原始实现 (所有模型从此开始)
def solve(problem):
n = problem["num_nodes"]
edges = problem["edges"]
# Build adjacency list
adj = [[] for _ in range(n)]
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
# DFS to count components
visited = [False] * n
count = 0
def dfs(node):
visited[node] = True
for neighbor in adj[node]:
if not visited[neighbor]:
dfs(neighbor)
for i in range(n):
if not visited[i]:
dfs(i)
count += 1
return {"number_connected_components": count}
性能:1.0x (基线)
进化后 - Gemini Flash 2.5 (200 次迭代):
def solve(problem):
n = problem.get("num_nodes", 0)
edges = problem.get("edges", [])
if n == 0:
return {"number_connected_components": 0}
# Build adjacency list with deque for O(1) operations
adj = [[] for _ in range(n)]
for u, v in edges:
adj[u].append(v)
adj[v].append(u)
# BFS with early termination and efficient tracking
visited = [False] * n
count = 0
from collections import deque
for start in range(n):
if visited[start]:
continue
# BFS for this component
queue = deque([start])
visited[start] = True
while queue:
node = queue.popleft()
for neighbor in adj[node]:
if not visited[neighbor]:
visited[neighbor] = True
queue.append(neighbor)
count += 1
return {"number_connected_components": count}
性能:95.78 倍加速比 关键优化
- 从 DFS 切换到 BFS
- 使用 deque 实现 O(1) 队列操作
- 增加提前终止检查
- 使用 get() 进行防御性编程
进化后 - Qwen3-Coder (100 次迭代):
def solve(problem):
n = problem["num_nodes"]
edges = problem["edges"]
# Union-Find approach - completely different algorithm!
parent = list(range(n))
def find(x):
if parent[x] != x:
parent[x] = find(parent[x]) # Path compression
return parent[x]
def union(x, y):
px, py = find(x), find(y)
if px != py:
parent[px] = py
# Process edges
for u, v in edges:
union(u, v)
# Count unique roots
return {"number_connected_components": len(set(find(i) for i in range(n)))}
性能:~25 倍加速比 关键洞察:不同模型发现了完全不同的算法!
- 带路径压缩的并查集
- 每个操作 O(α(n))(接近常数)
- 内存效率更高
示例 2:PSD 锥投影 - 增量优化
原始实现:
def solve(problem):
import numpy as np
A = np.array(problem["matrix"])
# Eigenvalue decomposition
eigenvalues, eigenvectors = np.linalg.eigh(A)
# Set negative eigenvalues to zero
eigenvalues[eigenvalues < 0] = 0
# Reconstruct matrix
A_psd = eigenvectors @ np.diag(eigenvalues) @ eigenvectors.T
return {"projected_matrix": A_psd.tolist()}
性能:1.0x (基线)
使用 Gemini Flash 2.5 Diffs 进化:
迭代 23
- eigenvalues[eigenvalues < 0] = 0
- A_psd = eigenvectors @ np.diag(eigenvalues) @ eigenvectors.T
+ # Vectorized operation
+ eigenvalues = np.maximum(eigenvalues, 0)
+ A_psd = eigenvectors @ np.diag(eigenvalues) @ eigenvectors.T
性能: 1.8x
迭代 67
- A_psd = eigenvectors @ np.diag(eigenvalues) @ eigenvectors.T
+ # Eliminate intermediate array
+ A_psd = (eigenvectors * eigenvalues) @ eigenvectors.T
性能: 15.2x
最终 (迭代 95)
def solve(problem):
import numpy as np
A = np.array(problem["matrix"])
w, v = np.linalg.eigh(A)
# One-line vectorized operation
A_psd = (v * np.maximum(w, 0)) @ v.T
return {"projected_matrix": A_psd.tolist()}
性能:32.7 倍加速比
示例 3:DCT 优化 - 趋同进化
原始:
def solve(problem):
import numpy as np
from scipy.fftpack import dct
signal = np.array(problem["signal"])
return {"dct": dct(signal, type=1).tolist()}
多个模型收敛到相同解决方案:
Gemini Flash 2.5
signal = np.array(problem["signal"], dtype=np.float64)
result = dct(signal, type=1, norm=None, overwrite_x=False)
Qwen3-Coder
signal = np.asarray(problem["signal"], dtype=np.float64)
return {"dct": dct(signal, type=1).tolist()}
关键发现:两者都独立发现了 dtype=np.float64 的优化!
- 两者都实现了 6.48 倍的加速比
- 表明存在最优解且可被发现
示例 4:SHA256 - 硬件限制
原始:
def solve(problem):
import hashlib
data = problem["data"].encode('utf-8')
hash_object = hashlib.sha256(data)
return {"hash": hash_object.hexdigest()}
最佳进化 (多个模型)
def solve(problem):
import hashlib
return {"hash": hashlib.sha256(problem["data"].encode()).hexdigest()}
性能:仅 1.1 倍加速比 学习:受硬件限制的操作优化潜力有限
模型比较
要全面了解所有 10 个独特测试模型的视图,请参见执行摘要仪表盘中的面板 C。完整的 29 个实验结果显示在上面的性能排名图表中。
特定任务性能热图
此热图显示了不同模型在特定 AlgoTune 任务上实现的加速因子。深红色表示更高的加速比。值得注意的模式:
- 计算连通分量显示出极大的差异(Flash 2.5 为 95x,而 Gemma 3 为 15x)
- PSD 投影在各模型中均实现了持续的高性能(32-42x)
- 像 SHA256 这样受硬件限制的任务,无论何种模型,改进都微乎其微
专业化与规模分析
Qwen3-Coder (480B MoE, 35B 激活) vs Qwen3-235B:
- 尽管“更大”(总参数 480B),Qwen3-Coder 只有 35B 激活参数
- 编码专业化带来了 68% 的性能提升(1.41x vs 0.84x)
- 证据表明训练数据和目标比规模更重要
按模型能力划分的进化策略
| 模型类型 | 最佳策略 | 证据 |
|---|---|---|
| 小型/弱型 (Flash Lite) | 完全重写 | diff 模式 0.79x vs 完整模式 1.10x |
| 强大编码 (Flash 2.5, Qwen3-Coder) | 基于 Diff | 1.64x vs 完整模式更低 |
| 通用目的 | 不一 | 依赖于模型 |
集成实验:为何更多模型 ≠ 更好结果
尽管结合了我们两个表现最好的模型(Gemini Flash 2.5 的 1.64x 和 Qwen3-Coder 的 1.41x),集成模型仅实现了 1.23x 的加速比——比任何一个单独的模型都差。
可视化指南:
- 面板 A:显示单个模型性能与集成性能对比——集成模型表现不如两者
- 面板 B:所有 30 个任务性能比较——Gemini、Qwen 和集成模型的完整性能概况
- 面板 C:进化过程比较——集成模型显示不规则振荡,而单一模型进展平稳
- 面板 D:按任务划分的模型一致性——3x30 热图显示每个任务的成对一致性,揭示冲突区域
关键发现:冲突的优化策略
集成模型失败是因为模型采用了不兼容的方法
- 计算连通分量:Gemini 使用 BFS,Qwen 使用并查集 → 振荡
- DCT 优化:不同的 dtype 策略 → 优化丢失
- 结果:与预期的 1.5-1.7x 相比,性能低了 19%
示例:算法冲突
# Iteration N: Gemini suggests BFS
queue = deque([start]) # BFS approach
# Iteration N+1: Qwen suggests Union-Find
parent = list(range(n)) # Different algorithm!
# Result: Hybrid mess that optimizes neither
观察到的集成失败模式
- 算法冲突:在同一任务中,BFS 与 Union-Find 方法的冲突
- 优化冲突:内存优化与计算优化的冲突
- 风格冲突:函数式与命令式代码模式的冲突
技术实现细节
OpenEvolve 配置
# Optimal configuration discovered
max_iterations: 200 # More is better
diff_based_evolution: true # For capable models
temperature: 0.4 # For Gemini, 0.6 for others
max_tokens: 16000 # Sweet spot
num_top_programs: 3
num_islands: 4
migration_interval: 20
migration_rate: 0.1
include_artifacts: true # Critical for performance
岛屿进化动态
- 4个岛屿保持多样性
- 每20次迭代进行迁移,防止过早收敛
- 每个岛屿可以发现不同的解决方案
- 全局追踪最佳程序
级联评估的优势
- 阶段1:快速语法/导入验证(< 1秒)
- 阶段2:小型测试用例(< 10秒)
- 阶段3:完整基准测试套件(< 60秒)
通过快速失败节省了约70%的评估时间。
实验中的关键观察
1. 按类型划分的性能改进
- 算法更改(DFS → BFS):观察到高达95倍的速度提升
- 矢量化优化:在矩阵运算中实现32倍的速度提升
- 微小代码更改(变量重命名、循环调整):通常< 2倍的速度提升
2. 模型解决方案的多样性
- 计算连通分量:Gemini 找到了 BFS 方法,Qwen 找到了 Union-Find 方法
- 矩阵运算:不同模型使用了不同的矢量化策略
- 大多数任务都发现了多种有效的优化路径
3. 进化策略性能
- 基于差异的进化与强大的编码模型:总体速度提升高达1.64倍
- 使用较弱模型进行完全重写:速度提升1.10倍(而使用差异方法为0.79倍)
- 模型能力决定了最佳策略
4. 迭代次数的影响
- 100次迭代:实现1.64倍的平均速度提升
- 200次迭代:2.04倍的平均速度提升(提升了24%)
- 在200次迭代过程中,性能持续提升
5. 参数效应
- 温度0.4:最佳单次运行(1.291倍),但方差较大
- 包含构件:观察到约17%的性能提升
- 令牌限制:16k与32k之间未显示显著差异
- 迁移率:在实验中0.1的表现优于0.2
6. 并行化影响
- 串行评估:0.396倍-0.585倍的速度提升(性能下降)
- 并行评估:相同配置下速度提升0.793倍-1.10倍
- 时间差异:13小时(串行)vs 0.9小时(并行)
结论
关键实验发现
- 迭代次数:200次迭代实现2.04倍速度提升,而100次迭代为1.64倍(提升24%)
- 模型专业化:Qwen3-Coder(编码专用模型)优于更大的通用模型
- 温度设置:结果各异 - 最佳单次运行在0.4,但观察到高方差
- 进化策略:基于差异的方法对强大的编码模型效果更好,完全重写对较弱的模型效果更好
- 并行化:串行评估使性能下降47-50%,时间增加14倍
- 集成结果:组合模型实现了1.23倍的速度提升,而单独模型分别为1.64倍和1.41倍
观察到的模式
- 模型发现了不同的算法方法(例如图问题的BFS与Union-Find)
- 受硬件限制的任务(SHA256)在所有配置中改进甚微
- 包含构件使性能提升约17%
- 在测试的配置中,0.1的迁移率比0.2表现更好