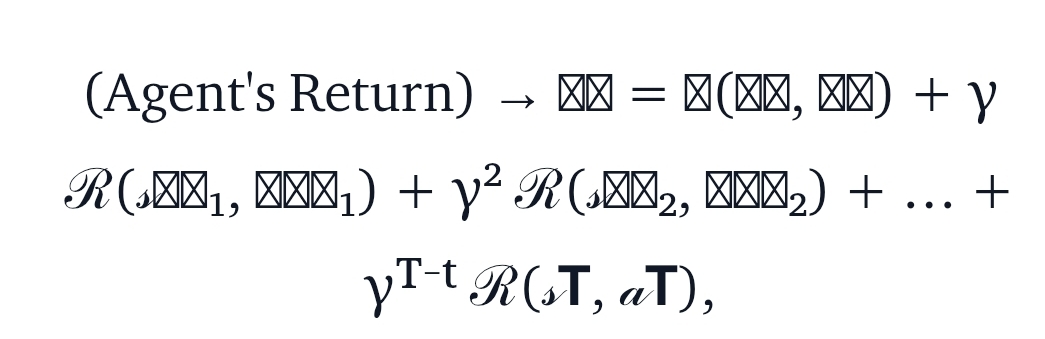Bourbaki (7b): 面向普特南基准（第一部分：推理 MDPs）的 SOTA 7B 算法

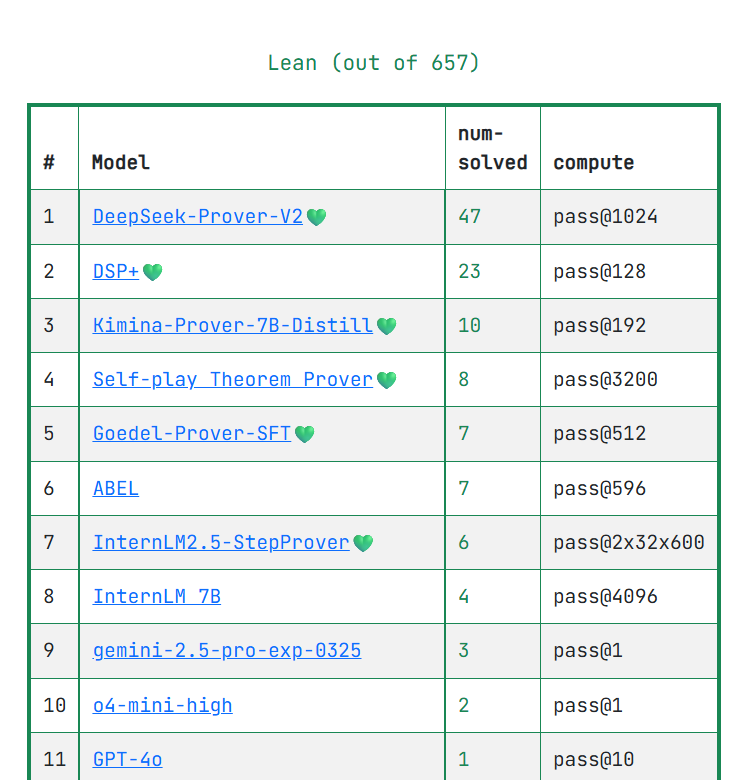
对于 LLMs 来说，推理仍然是一个开放的挑战。在我看来，衡量推理能力最好的方法之一是让 LLMs 执行数学证明。在这方面，我认为 PutnamBench 是一个了不起的测试——它要求 LLMs 证明大学水平的问题。PutnamBench 的作者在阐明这些问题的重要性及其难度方面做得非常出色。鉴于其难度，在排行榜上，最好的模型（DeepSeek-Proverv2 671B）仅能用 Lean 证明 657 个问题中的 47 个，而最好的 7B 模型（Kimina-Distil）只能证明 10 个，这并不令人惊讶。这项任务非常艰巨！！

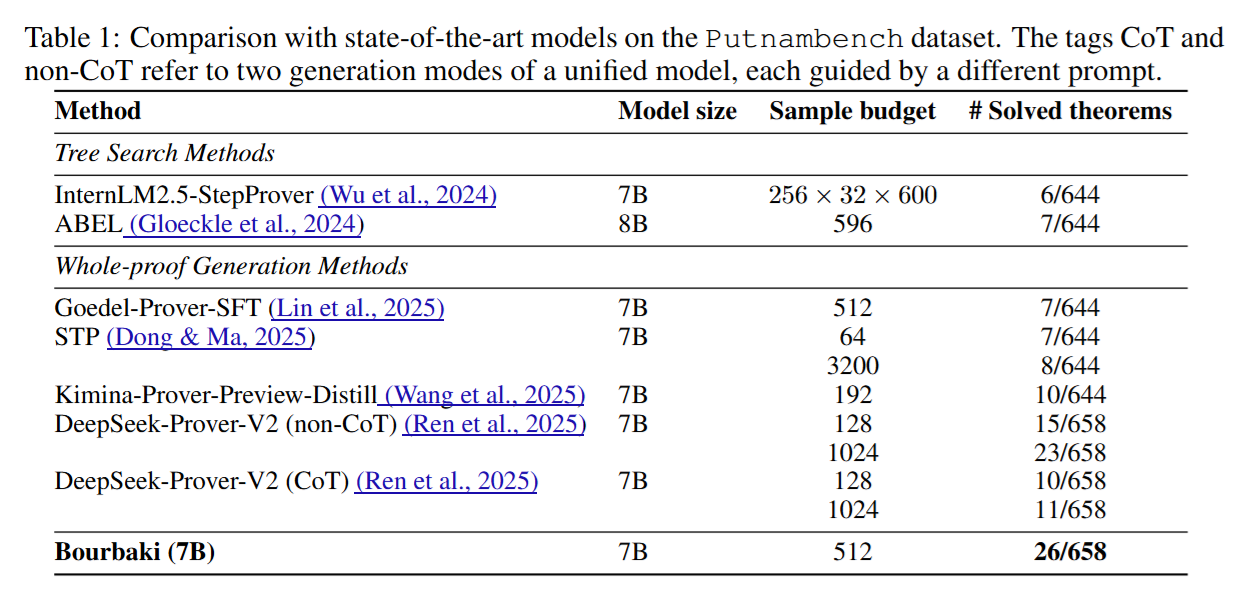
在我们最近的论文中，我们引入了 Bourbaki (7b)，这是一种在奖励非常稀疏的环境中有效搜索证明的 LLMs 算法。我们的搜索利用了我们提出的一种蒙特卡洛树搜索（MCTS）变体，它近似于我们称之为自生成目标条件 MDPs（sG-MDPs）的解决方案。sG-MDPs 是一种新型 MDPs，其中智能体根据不断演变的证明状态生成并追求其子目标。鉴于这种更结构化的目标生成，所产生的问题更易于搜索。在这里，我们可以应用类似 MCTS 的算法来解决 sG-MDP，在 Bourbaki (7b) 中实例化我们的方法，这是一个可以集成多个 7B LLMs 进行子目标生成和策略合成的模块化系统。在 PutnamBench 上，Bourbaki (7b) 解决了 26 个问题，在此规模的模型中取得了新的 SOTA 结果。

为什么是系列博客： 好吧，我想努力让每个人都理解 Bourbaki (7b) 是什么以及它做什么。我不想只是给你一个带有结果宣传的 ChatGPT 摘要。Bourbaki (7b) 是一个好的开始，我相信它是我们进行证明时应该采取的正确途径之一。我希望通过更多的曝光，除了实验和代码之外，一些人会感兴趣并帮助我们改进它！在本系列的第一篇博客中，我们将讨论基础知识：1) MCTS 以及为什么它应该应用于 LLMs，这样整个世界就不会只是用 10 个数据点微调一个 100000000000000000000000 b 模型（并不是我以前没做过 :-P ），2) MDPs 的基础知识，以及 3) 香草 MCTS 算法。

让我们开始： 蒙特卡洛树搜索 (MCTS) 是一种用于做出最佳决策的启发式方法。它在选择众多的领域中受益匪浅，例如游戏、规划和基于模型的优化问题。虽然 MCTS 背后的概念已经存在了几十年，但由于其在游戏 AI 中的成功，该方法在 2010 年代中期获得了广泛关注，例如 AlphaGo，它使用 MCTS 在围棋游戏中击败了专业人类玩家。此外，MCTS 已在机器人学、自动化规划甚至药物发现中找到应用。这些成功以及 MCTS 在无需暴力搜索的情况下处理大型搜索空间的有效性使其成为现代 AI 的宝贵工具。

在 2010 年代和 2020 年代初期，随着大规模神经网络、大型计算集群和互联网规模数据的出现，人工智能从电脑游戏毕业，掌握了类人文本生成。这一时期见证了大型语言模型（LLMs）的兴起，它们利用海量数据集和数十亿参数在自然语言处理任务中取得了前所未有的表现。这些模型展示了生成连贯、上下文相关文本的卓越能力，使它们成为重塑学术界、工业界乃至人类的变革性工具，我敢说。

为什么 MCTS 适用于 LLMs： 尽管 LLMs 在生成流畅且与上下文相关的回复方面表现出色，但它们在需要长期规划、推理或探索复杂决策空间的任务中面临挑战。这种行为不足为奇，因为这些模型主要通过下一个词元预测进行训练。它们的目标是根据先前的上下文生成下一个最可能的词元，而不是进行战略性思考或朝着特定目标努力。因此，它们可能不会进行目标条件推理，而是专注于生成局部合理但可能缺乏逻辑一致性的输出。例如，在解决复杂的数学问题或在类似游戏的设置中做出战略决策时，LLMs 可能会生成局部合理的输出，但缺乏全局最优性。

这是蒙特卡洛树搜索可以在 LLMs 中发挥关键作用的地方。通过将 MCTS 整合到 LLMs 的推理和决策过程中，可以探索多个潜在的延续、模拟它们的结果，并利用这些模拟来指导生成过程。MCTS 提供了一种潜在的实用方法来导航语言生成的巨大搜索空间，平衡探索创造性可能性和利用满足相关目标的有前途的路径。将 MCTS 与 LLMs 结合起来，为以下方面打开了机会：

1. 改进规划： MCTS 可以帮助 LLMs 提前评估多个步骤，确保决策与长期目标或约束保持一致；
2. 提高连贯性： 通过模拟和评估不同分支的结果，MCTS 减少了生成文本中矛盾或不一致的风险；
3. 优化推理： MCTS 允许 LLMs 探索各种问题解决策略并确定最有效的方法；以及
4. 处理大型动作/令牌空间： MCTS 可以系统地探索巨大的词汇表和可能的序列，重点关注最有希望的选项。

MCTS 和 LLMs 之间的这种协同作用有潜力解决当前语言模型中的关键限制，使它们能够以更高的精度和可靠性处理更复杂的、多步骤的推理任务。

回到 MDPs：

为了更好地理解这一切是如何运作的，让我们回到标准的马尔可夫决策过程 (MDPs) 并了解 MCTS 如何用于解决它们。虽然 MCTS 可以并且已经更广泛地应用，但在本教程中，我们将主要关注序贯决策问题，这些问题最好被形式化为马尔可夫决策过程，简称 MDPs。MDP 由以下元组定义：ℳ = ⟨𝒮, 𝒜, ℛ, 𝒫, γ⟩，其中

• 𝒮 (状态): 智能体可能遇到的所有可能情况——例如，对我们来说是令牌历史。
• 𝒜 (行动): 智能体可以采取的所有可能行动——例如，下一个令牌或步骤。
• ℛ (奖励): 根据所采取的行动向智能体提供反馈的函数——例如，我们是否得到了数学问题的正确解决方案？
• 𝒫 (转移概率): 给定一个行动，从一个状态转移到另一个状态的概率——例如，在我们的例子中是确定性的（将新行动附加到历史记录）。
• γ (折扣因子): 决定未来奖励的重要性——例如，0.99 左右。

在 MDP 中，一个配备策略的智能体随着时间步长与环境交互。策略 π: 𝒮 × 𝒜 → [0,1] 是一种行动选择策略，它为在状态 s 中选择行动 a 分配概率。在每个时间步长 t，智能体观察当前状态 𝓈ₜ，根据其策略 𝒶ₜ ∼ π(⋅|𝓈ₜ) 选择一个行动，并作为奖励 ℛ(𝓈ₜ,𝒶ₜ) 接收反馈。通过这种方式，环境根据 𝓈ₜ₊₁ ∼ 𝒫(⋅|𝓈ₜ,𝒶ₜ) 转移到新状态，并重复上述过程。智能体的目标是最大化其轨迹中累积的奖励

我们定义给定时间步的累积奖励（回报）如下：

其中 T 是时间范围长度或终止时间步长。这个方程捕捉了智能体决策不仅应关注即时奖励，还应考虑未来奖励 ℛ(𝓈ₜ₊₁, 𝒶ₜ₊₁)、ℛ(𝓈ₜ₊₂, 𝒶ₜ₊₂) 等的想法。折扣因子 γ 平衡了即时奖励和未来奖励的重要性，因为

• 即时奖励： 第一项表示智能体对其当前行动收到的直接反馈。它的权重更高（γ⁰ =1），因为它直接反映了在时间 t 所做决策的质量。
• 未来奖励： 后续项表示智能体可以从未来决策中获得的预期奖励。γ 的幂次方对这些奖励进行加权。这意味着当 γ <1 时，未来更远的奖励对当前决策的影响较小，因为 γ² > γ³ > γ⁴ > …

当然，我们智能体的目标是找到最优的行动选择规则（或策略），以最大化这些回报。在此之前，我们首先需要一个度量来评估状态或行动在策略 π(⋅|𝓈ₜ) 下的“好坏”。如果配备了这种度量，我们就可以优化出最大化它的最佳策略。为了量化这种“好坏”，我们定义了两个函数：价值函数，用于评估从某个状态开始的预期回报；以及 Q-函数，用于评估从某个状态开始并采取特定行动的预期回报。

• 价值函数： 价值函数 𝓥^π(𝓈) = ℰ_{π,𝒫}[𝓖ₜ | 𝓈ₜ = 𝓈]，提供了在给定策略 π 下衡量状态 𝓈 “好坏”的度量。它表示智能体如果从状态 𝓈 开始并随后遵循策略 π，可以实现的预期累积奖励。这个函数包含了智能体在 𝓈 中可能获得的即时奖励，以及通过 π 指导的未来行动可以累积的长期奖励。价值函数对于评估状态的整体 desirability 是有益的。如果一个智能体可以比较不同状态的价值，它就可以优先考虑那些有望在长期内带来更高回报的状态。
• Q-函数： Q-函数 𝓠^π(𝓈, 𝒶) 提供了在给定策略 π 下，在状态 𝓈 中采取特定行动 𝒶 “好坏”的度量。它表示智能体通过在状态 𝓈 中采取行动 𝒶，并在所有后续行动中遵循策略 π，可以实现的预期累积奖励。虽然价值函数评估状态的整体吸引力，但 Q-函数将这种评估扩展到包括特定行动，使其在行动选择中特别有用。通过比较同一状态中不同行动的 Q-值，智能体可以确定哪些行动将带来更高的回报。我们将 𝓠^π(𝓈, 𝒶) 定义为
  (Q-函数) → 𝓠^π(𝓈, 𝒶) = ℰ_{π,𝒫}[𝓖ₜ | 𝓈ₜ = 𝓈, 𝒶ₜ = 𝒶]。
  这里，期望是根据 π 诱导的状态和行动轨迹，从 𝓈ₜ = 𝓈 和 𝒶ₜ = 𝒶 开始。

智能体必须识别出最大化长期奖励的最优策略，记为 π。最优策略做出决策以最大化每个状态的预期回报。价值函数 𝓥^π(𝓈) 和 Q-函数 𝓠^π(𝓈, 𝒶) 在定义和寻找最优策略中都起着作用。更具体地说，最优策略 π 可以从最优 Q-函数 𝓠^★(𝓈, 𝒶) 中导出，如下所示：

最优 Q 函数 𝓠^★(𝓈, 𝒶) 满足以下条件

这个方程简单地说明，在状态 𝓈 中采取行动 𝒶 的最优 Q 值等于即时奖励 ℛ(𝓈, 𝒶) 加上下一个状态 𝓈' 的折扣最大预期 Q 值（即，我们未来会得到什么）。折扣因子 γ 决定了未来奖励的重要性。

虽然 Q 函数评估特定动作在给定状态下的质量，但状态本身的整体质量（独立于任何特定动作）则由最优价值函数 𝓥^★(𝓈) 捕捉。此函数通过选择最佳可能动作来总结从状态 𝓈 可实现的最大预期回报。形式上，𝓥^★(𝓈) 定义为

这个方程，被称为 𝓥^★(𝓈) 的贝尔曼最优性方程，强调了状态的价值取决于即时奖励 ℛ(𝓈, 𝒶) 和预期的未来奖励，并由转移概率和折扣因子 γ 加权。

MCTS 算法

既然我们已经定义了最优价值函数和最优 Q 函数，接下来的挑战是找到通过近似这些项来解决 MDP 的方法。虽然有多种方法可以解决这个问题，但在本博客中，我们主要关注基于规划的方法，更具体地说是 MCTS。MCTS 在规划方面特别有效，因为它通过模拟逐步构建搜索树以近似价值函数和 Q 函数。为了理解 MCTS 在 MDP 上下文中的运作方式，将其组件映射到 MDP 框架的组件是很有用的

但那是棵什么树——如何将 MDP 映射到搜索树： 在深入研究算法如何搜索树中的最优遍历之前，我们需要了解要构建哪种树以及它如何映射到我们上面定义的 MDP。让我们开始吧！

1. 状态作为搜索树中的节点： 在 MCTS 中，搜索树中的每个节点都对应于 MDP 的一个状态 𝓈 ∈ 𝒮。树的根节点表示起始状态，其他节点表示从根通过一系列行动可到达的状态。例如，这些节点还存储统计相关信息，以方便搜索最优策略。这些统计信息可以包括当前状态的访问次数和累积奖励，可用于估计 Q 值等。
2. 动作作为节点之间的边： 如前所述，在 MDP 中，动作 𝒶 ∈ 𝒜 允许环境根据 𝓈′ ∼ 𝒫(⋅|𝓈, 𝒶) 从状态 𝓈 转移到后继状态 𝓈′。在 MCTS 中，这些动作映射到树中的边。每条边代表从 𝓈 采取的特定动作 𝒶，导致一个新的状态（或树中的节点） 𝓈′。树搜索将根据存储在节点中的估计 Q 值 𝓠(𝓈, 𝒶) 和访问计数来选择边（或动作），平衡探索（尝试较少访问的状态）和利用（偏好具有更高累积奖励估计的动作）。
3. 回报和转换用于展开： MCTS 在搜索最优策略时执行模拟或展开。在模拟过程中，MCTS 算法根据 𝒫(⋅|𝓈, 𝒶) 采样 𝓈′ 并累积奖励以估计回报 𝓖ₜ。因此，这些展开在近似 𝓠(𝓈, 𝒶) 中起着关键作用，其结果用于更新存储在树节点中的值估计。

---

香草算法： MCTS 是一种迭代算法，它逐步构建搜索树以近似最优价值函数和最优策略。从高层次上看，它模拟轨迹（rollouts），遵循环境模型，从奖励函数 ℛ 收集奖励，并随着时间的推移细化价值估计。具体来说，该算法包含四个主要步骤：1) 选择，2) 扩展，3) 模拟，和 4) 反向传播。

1) 选择阶段： 从根节点（初始状态 𝓈₀）开始，算法通过选择子节点（后续状态）遍历搜索树，其选择依据的策略平衡了探索和利用。一种常见的选择策略是树的上限置信度（Upper Confidence Bound for Trees），我们简称它为 UCT，它是对上限置信度的改编：

其中 UCT(𝓈, 𝒶) 有两项，一项负责利用，另一项负责探索，其定义基于访问统计数据

其中 β 是权衡探索与利用的参数，N(𝓈) 是状态 𝓈 的访问次数，N(𝓈, 𝒶) 是在状态 𝓈 中应用动作 𝒶 的次数，ln 是自然对数。

这个 UCT 公式旨在处理探索-利用困境，这直观地归结为回答以下问题：我应该依赖我已知的信息，还是应该寻找新的可能性？

在我们的例子中，如果算法只利用（仅根据 𝓠(𝓈, 𝒶) 选择行动），它就有可能错过那些尚未充分探索的更好行动。另一方面，如果它探索过多，它就会在（可能）无用的行动上花费过多时间，损害其收敛到最佳策略。通过将 𝓠(𝓈, 𝒶) 与探索奖励相结合，UCT 可以动态调整其行为。为了理解这一点，让我们更详细地研究这个方程，并将我们的分析分为两个阶段：搜索的早期和后期。

在搜索开始时，探索项 √(ln [N(𝓈)/N(𝓈, 𝒶)]) 占主导地位，因为在状态 𝓈 中执行动作 𝒶 的次数，即 N(𝓈, 𝒶) 很小。这确保了尝试频率较低的动作获得更高的探索奖励，鼓励算法尝试它们。请注意，分子以 N(𝓈) 的对数形式增长，这确保即使状态 𝓈 被访问多次，探索奖励也不会增长过快。此外，分母 N(𝓈, 𝒶) 最初非常小，极大地提升了奖励，确保每个动作至少被尝试一次。

在搜索的后期，随着动作在状态 𝓈 中被更频繁地尝试，N(𝓈, 𝒶) 变得更大，从而减少了探索项 β√(ln [N(𝓈)/N(𝓈, 𝒶)])。在此阶段，Q 值估计 𝓠(𝓈, 𝒶) 项占主导地位，鼓励算法偏爱过去模拟中估计奖励最高的动作。换句话说，它促使我们的算法利用其先前的知识，而不仅仅是探索。这反映了算法对其 Q 值估计的信心日益增加，因为该动作已经采样了足够多次。

2) 扩展阶段： 在选择阶段确定一个叶节点（一个尚未完全探索的节点）后，算法进入扩展阶段。扩展旨在通过添加一个或多个子节点来增长搜索树，这些子节点代表从所选叶节点可到达的状态。换句话说，上面描述的 UCT 方法通常在已扩展的节点上操作。当它到达一个叶节点时，扩展就开始了。这个阶段逐步构建搜索树。

在扩展阶段，算法检查所选叶节点处的可用操作。具有相应子节点的操作会被忽略，因为它们已在先前的迭代中被探索。从剩余的未探索操作中，算法选择一个操作进行扩展。这种选择通常是随机的或基于启发式的。一旦选择了操作，算法就会模拟环境以确定该操作导致的下一个状态。一个新的子节点被添加到树中，表示这个新达到的状态。新子节点使用默认统计数据进行初始化。具体来说，其访问计数 N(𝓈') 设置为零。新节点处所有可能操作的估计 Q 值也设置为零。随着更多模拟通过此节点，这些值将在模拟和反向传播阶段进行更新。

3) 模拟阶段： 这是 MCTS 过程的第三步，对于估计新扩展节点的价值至关重要。一旦在扩展阶段将新节点添加到树中，模拟阶段就用于通过从该状态到终止状态（或直到预定义的深度）运行模拟轨迹或展开来评估相应状态的潜力。模拟阶段的主要目标是近似从新添加状态开始获得的累积奖励（或回报）。在模拟阶段，算法从新扩展的节点开始，该节点代表特定状态 𝓈。从这个状态开始，它通过根据展开策略重复选择动作来模拟轨迹。这种展开策略，也称为默认策略，通常比树本身中使用的基于 UCT 的选择策略更简单，因为模拟阶段需要快速运行以避免成为计算瓶颈。展开策略的常见选择包括随机策略或启发式策略。算法选择动作并模拟转换，直到达到终止状态或预定义的​​最大深度。在模拟结束时，算法计算轨迹的回报 𝓖ₜ。

4) 反向传播阶段： 这是 MCTS 的最后阶段，根据模拟阶段的结果更新搜索树中节点和边的统计数据。反向传播的主要目的是将模拟轨迹的结果从新扩展的节点反向传播到根节点，以便这些更新可以指导未来的迭代。请注意，在模拟过程中，我们通常不会向树中添加新节点，以避免内存爆炸。在计算从模拟获得的 𝓖ₜ 后，反向传播从新扩展的节点开始。累积回报 𝓖ₜ 沿着选择阶段遍历的路径向上回传到树中。在此路径上的每个节点，访问计数 N(𝓈) 和动作访问计数 N(𝓈, 𝒶) 都会增加。此外，Q 值 𝓠(𝓈, 𝒶) 会更新以反映从展开中获得的新信息。通常，我们使用以下增量公式更新这些 Q 值：

如果有错别字，请留言！我会修复它们 :-) 在下一篇文章中，我们将详细介绍如何将定理证明重新构建为（目标条件）MDPs，敬请期待！