使用 Hugging Face Transformers、Accelerate 和 bitsandbytes 对大规模 transformers 进行 8 位矩阵乘法的温和介绍

导言
语言模型正在变得越来越大。撰写本文时,PaLM 拥有 5400 亿参数,OPT、GPT-3 和 BLOOM 拥有约 1760 亿参数,而且我们正朝着更大的模型发展。下图显示了一些近期语言模型的大小。
因此,这些模型难以在易于获取的设备上运行。例如,仅在 BLOOM-176B 上进行推理,您就需要 8 个 80GB A100 GPU(每个约 15,000 美元)。要微调 BLOOM-176B,您需要 72 个这样的 GPU!更大的模型,如 PaLM,将需要更多的资源。
由于这些庞大的模型需要如此多的 GPU 才能运行,我们需要寻找方法来减少这些需求,同时保持模型的性能。已经开发了各种技术来缩小模型大小,您可能听说过量化和蒸馏,还有许多其他技术。
完成 BLOOM-176B 的训练后,HuggingFace 和 BigScience 的我们正在寻找方法,使这个大型模型更容易在更少的 GPU 上运行。通过我们的 BigScience 社区,我们了解到 Int8 推理的研究,该研究不会降低大型模型的预测性能,并将大型模型的内存占用减少 2 倍。很快,我们开始合作进行这项研究,最终将其完全集成到 Hugging Face transformers 中。通过这篇博客文章,我们为所有 Hugging Face 模型提供了 LLM.int8() 集成,我们将在下面更详细地解释。如果您想了解更多关于我们研究的信息,您可以阅读我们的论文《LLM.int8():大规模 Transformer 的 8 位矩阵乘法》。
本文重点对这种量化技术进行高层次概述,阐述将其纳入 transformers 库的困难,并制定这种合作的长期目标。
在这里您将了解到,究竟是什么让大型模型占用如此多的内存?是什么让 BLOOM 达到 350GB?让我们先逐步了解一些基本前提。
机器学习中常用的数据类型
我们首先基本理解不同的浮点数据类型,在机器学习语境中也称为“精度”。
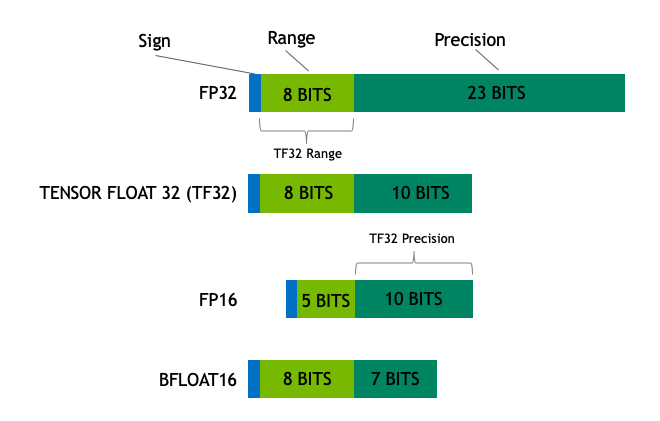
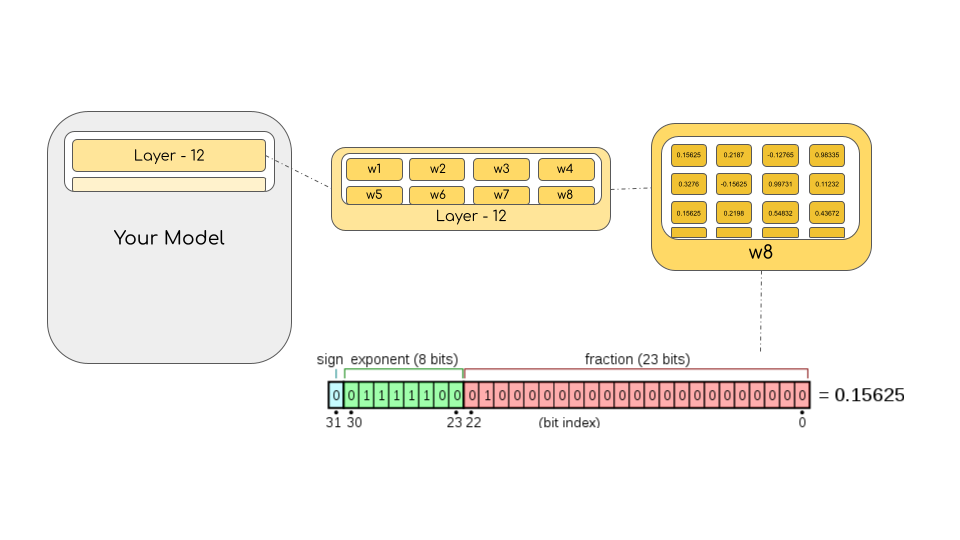
模型的大小取决于其参数的数量及其精度,通常为 float32、float16 或 bfloat16(下图来自:https://blogs.nvidia.com/blog/2020/05/14/tensorfloat-32-precision-format/)。
Float32(FP32)代表标准化的 IEEE 32 位浮点表示。使用这种数据类型可以表示广泛的浮点数。在 FP32 中,8 位保留给“指数”,23 位保留给“尾数”,1 位保留给数字的符号。除此之外,大多数硬件都支持 FP32 操作和指令。
在 float16(FP16)数据类型中,5 位保留给指数,10 位保留给尾数。这使得 FP16 数字的可表示范围远低于 FP32。这使得 FP16 数字面临溢出(尝试表示一个非常大的数字)和下溢(表示一个非常小的数字)的风险。
例如,如果您执行 10k * 10k,最终得到 100M,这在 FP16 中无法表示,因为最大可能数字为 64k。因此,您将得到 NaN(非数字)结果,如果您像神经网络那样进行顺序计算,所有先前的工作都将被破坏。通常,使用损失缩放来克服这个问题,但它并不总是有效。
为了避免这些限制,创建了一种新格式 bfloat16 (BF16)。在 BF16 中,8 位用于指数(与 FP32 相同),7 位用于小数部分。
这意味着在 BF16 中,我们可以保留与 FP32 相同的动态范围。但是我们相对于 FP16 损失了 3 位精度。现在对于大数字绝对没有问题,但这里的精度比 FP16 更差。
在 Ampere 架构中,NVIDIA 还引入了 TensorFloat-32 (TF32) 精度格式,结合了 BF16 的动态范围和 FP16 的精度,仅使用 19 位。目前它仅在某些操作内部使用。
在机器学习术语中,FP32 称为全精度(4 字节),而 BF16 和 FP16 称为半精度(2 字节)。除此之外,int8(INT8)数据类型由 8 位表示组成,可以存储 2^8 种不同的值(对于有符号整数,介于 [0, 255] 或 [-128, 127] 之间)。
虽然理想情况下训练和推理应以 FP32 进行,但它比 FP16/BF16 慢两倍,因此采用混合精度方法,其中权重以 FP32 形式作为精确的“主权重”参考,而前向和后向传递中的计算则以 FP16/BF16 进行,以提高训练速度。然后使用 FP16/BF16 梯度更新 FP32 主权重。
在训练过程中,主权重始终以 FP32 存储,但实际上,半精度权重在推理过程中通常能提供与其 FP32 对应物相似的质量——只有当模型接收到多个梯度更新时才需要模型的精确参考。这意味着我们可以使用半精度权重,并使用一半的 GPU 来达到相同的效果。
要计算模型的字节大小,需要将参数数量乘以所选精度的字节大小。例如,如果我们使用 BLOOM-176B 模型的 bfloat16 版本,我们有 176*10**9 x 2 字节 = 352GB!如前所述,将其放入少量 GPU 中是一个相当大的挑战。
但是,如果我们能使用不同的数据类型,用更少的内存存储这些权重呢?一种称为量化的方法已广泛用于深度学习中。
模型量化介绍
实验表明,我们发现使用 2 字节的 BF16/FP16 半精度,可以获得几乎相同的推理结果,而模型大小减半。如果能进一步压缩就太棒了,但在较低精度下推理质量开始急剧下降。
为了弥补这一点,我们引入了 8 位量化。这种方法使用四分之一精度,因此只需要模型大小的 1/4!但它不是通过简单地丢弃一半的比特来完成的。
量化是通过从一种数据类型“四舍五入”到另一种数据类型来完成的。例如,如果一种数据类型的范围是 0..9,另一种是 0..4,那么第一种数据类型中的值“4”将四舍五入为第二种数据类型中的“2”。但是,如果我们在第一种数据类型中得到值“3”,它介于第二种数据类型的 1 和 2 之间,那么我们通常会四舍五入为“2”。这表明第一种数据类型中的值“4”和“3”在第二种数据类型中具有相同的值“2”。这突出表明,量化是一个嘈杂的过程,可能导致信息丢失,一种有损压缩。
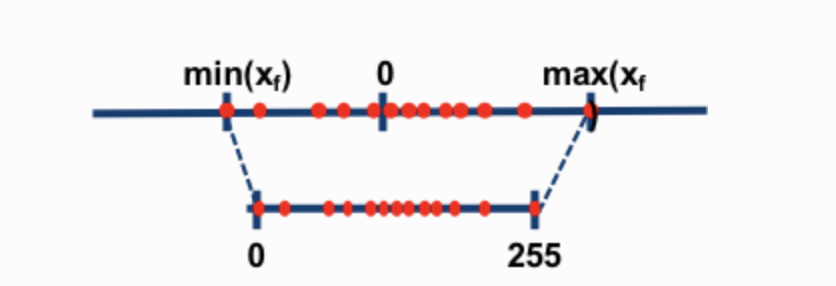
两种最常见的 8 位量化技术是零点量化和绝对最大值(absmax)量化。零点量化和 absmax 量化将浮点值映射到更紧凑的 int8(1 字节)值。首先,这些方法通过量化常数对其输入进行缩放来对其进行归一化。
例如,在零点量化中,如果我的范围是 -1.0…1.0,并且我想量化到 -127…127 的范围,我需要乘以 127 的因子,然后将其四舍五入到 8 位精度。要检索原始值,您需要将 int8 值除以相同的量化因子 127。例如,值 0.3 将被缩放为 0.3*127 = 38.1。通过四舍五入,我们得到 38。如果我们反转这个过程,我们得到 38/127=0.2992 – 在此示例中,我们有 0.008 的量化误差。这些看似微小的误差会随着它们在模型层中传播而累积和增长,从而导致性能下降。
(图片取自:这篇博客文章)
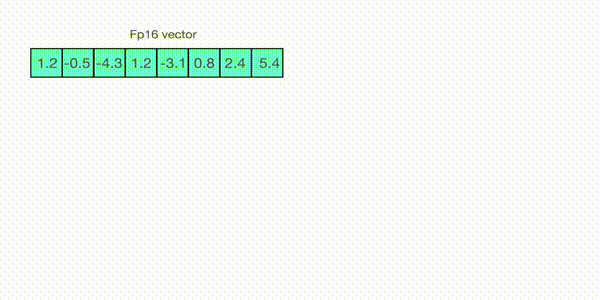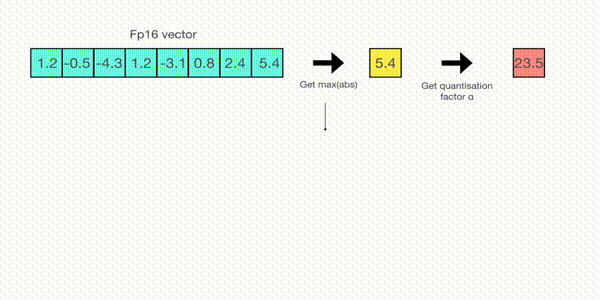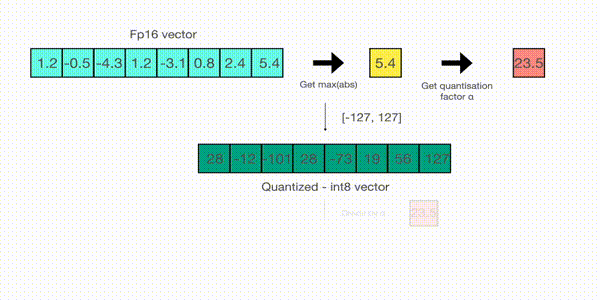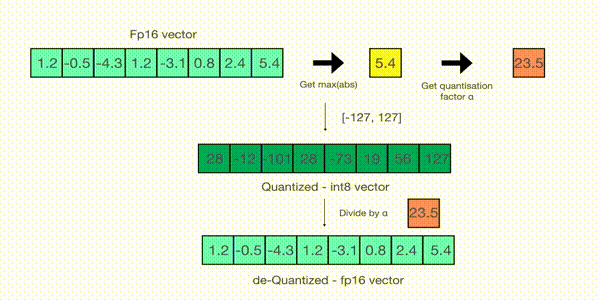
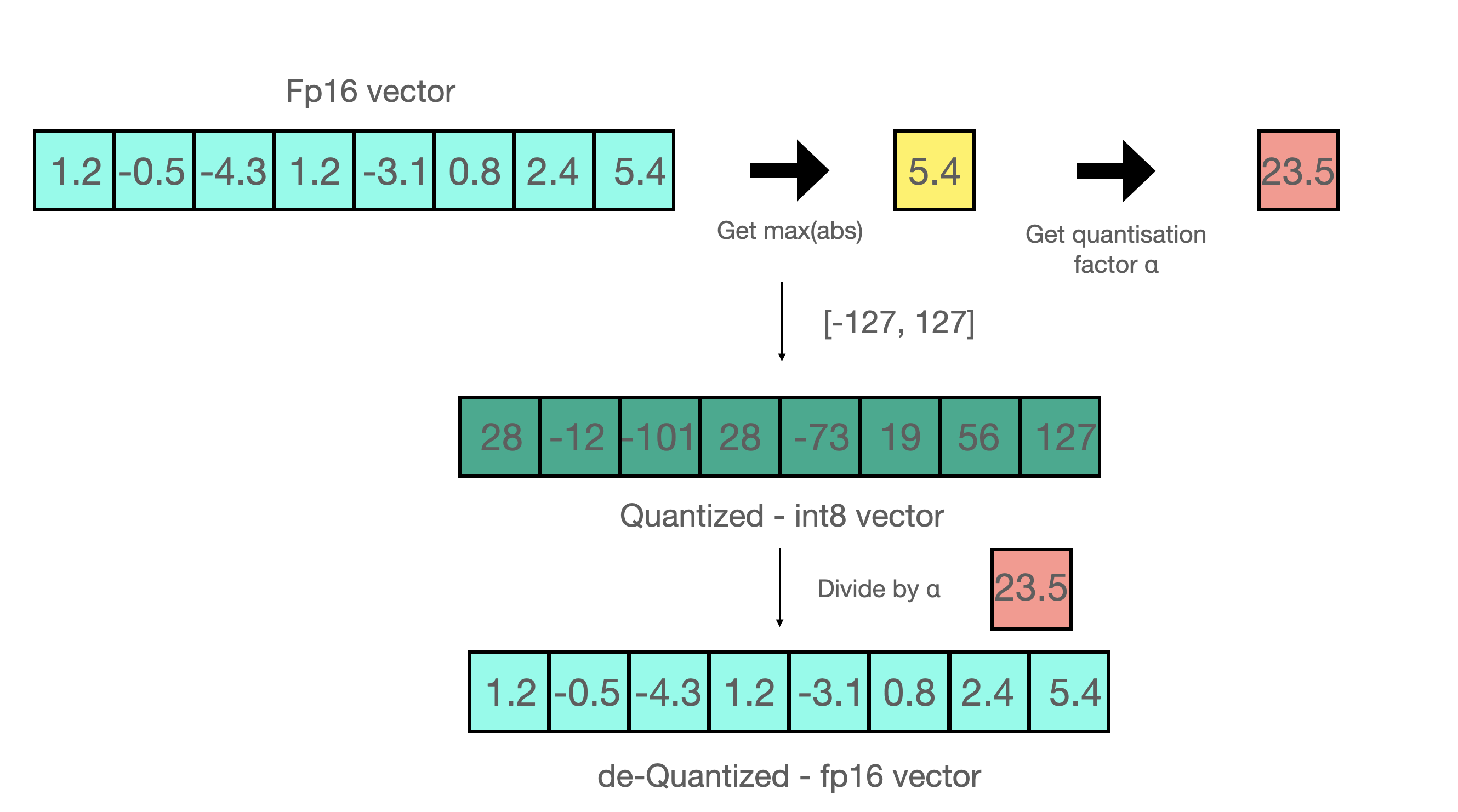
现在让我们看看 absmax 量化的细节。要计算 fp16 数及其在 absmax 量化中对应的 int8 数之间的映射,您必须首先除以张量的绝对最大值,然后乘以数据类型的总范围。
例如,假设您想在包含 [1.2, -0.5, -4.3, 1.2, -3.1, 0.8, 2.4, 5.4] 的向量中应用 absmax 量化。您从中提取绝对最大值,在本例中为 5.4。Int8 的范围是 [-127, 127],因此我们将 127 除以 5.4,得到 23.5 作为缩放因子。因此,将原始向量乘以它会得到量化向量 [28, -12, -101, 28, -73, 19, 56, 127]。
要检索最新的,只需用全精度将 int8 数除以量化因子即可,但由于上述结果是“四舍五入”的,因此会损失一些精度。
对于无符号 int8,我们将减去最小值并按绝对最大值缩放。这与零点量化的做法接近。它类似于 min-max 缩放,但后者以保持值尺度的方式进行,使得值“0”始终由整数表示,而没有任何量化误差。
这些技巧可以通过多种方式组合,例如,在矩阵乘法中进行逐行或逐向量量化,以获得更准确的结果。观察矩阵乘法 A*B=C,与通过每个张量的绝对最大值进行归一化的常规量化不同,逐向量量化找到 A 的每一行和 B 的每一列的绝对最大值。然后,我们通过除以这些向量来归一化 A 和 B。然后我们计算 A*B 得到 C。最后,为了恢复 FP16 值,我们通过计算 A 和 B 的绝对最大值向量的外积来进行反归一化。有关此技术的更多详细信息,请参阅 LLM.int8() 论文 或 Tim 博客上关于 量化和涌现特征的博客文章。
虽然这些基本技术使我们能够量化深度学习模型,但它们通常会导致大型模型精度下降。我们集成到 Hugging Face Transformers 和 Accelerate 库中的 LLM.int8() 实现是第一种即使对于拥有 176B 参数(例如 BLOOM)的大型模型也不会降低性能的技术。
LLM.int8() 温和总结:大型语言模型的零精度损失矩阵乘法
在 LLM.int8() 中,我们已经证明,为了理解为什么传统量化在大型模型中失败,理解 transformer 的规模依赖涌现特性至关重要。我们证明,性能下降是由异常特征引起的,我们将在下一节中解释。LLM.int8() 算法本身可以解释如下。
本质上,LLM.int8() 旨在通过三个步骤完成矩阵乘法计算
- 从输入隐藏状态中,按列提取异常值(即大于某个阈值的值)。
- 以 FP16 格式对异常值进行矩阵乘法,并以 int8 格式对非异常值进行矩阵乘法。
- 对非异常值结果进行反量化,并将异常值和非异常值结果相加,以获得 FP16 格式的完整结果。
这些步骤可以总结为以下动画
异常特征的重要性
异常值通常指超出某些数字全局分布范围的值。异常值检测已在现有文献中广泛使用和涵盖,并且事先了解特征的分布有助于异常值检测任务。更具体地说,我们观察到大规模经典量化对于基于 transformer 的模型(参数大于 6B)失败。虽然小型模型中也存在大型异常特征,但我们观察到,达到某个阈值后,这些异常值会形成高度系统化的模式,这些模式存在于 transformer 的每一层中。有关这些现象的更多详细信息,请参阅 LLM.int8() 论文 和 关于量化和涌现特征的博客文章。
如前所述,8 位精度受到极大限制,因此对包含多个大值的向量进行量化可能会产生严重错误的結果。此外,由于基于 Transformer 的架构的内置特性将所有元素连接在一起,这些误差在通过多层传播时会趋于复合。因此,为了促进对这些极端异常值进行高效量化,开发了混合精度分解技术。接下来将对此进行讨论。
MatMul 内部
计算完隐藏状态后,我们使用自定义阈值提取异常值,并如上所述将矩阵分解为两部分。我们发现,以这种方式提取所有大小为 6 或更大的异常值可以恢复完整的推理性能。异常值部分以 fp16 完成,因此它是经典的矩阵乘法,而 8 位矩阵乘法通过使用向量量化将权重和隐藏状态量化为 8 位精度——即,隐藏状态逐行量化,权重矩阵逐列量化。在此步骤之后,结果被反量化并以半精度返回,以便将其添加到第一次矩阵乘法中。
0 精度损失意味着什么?
我们如何正确评估这种方法的性能下降?在使用 8 位模型时,我们在生成质量方面损失了多少?
我们使用 lm-eval-harness 运行了几个常见基准测试,并报告了 8 位模型和原生模型的结果。
对于 OPT-175B
| 基准 | - | - | - | - | 差异 - 值 |
|---|---|---|---|---|---|
| 名称 | 指标 | 值 - int8 | 值 - fp16 | 标准误差 - fp16 | - |
| hellaswag | acc_norm | 0.7849 | 0.7849 | 0.0041 | 0 |
| hellaswag | acc | 0.5921 | 0.5931 | 0.0049 | 0.001 |
| piqa | acc | 0.7965 | 0.7959 | 0.0094 | 0.0006 |
| piqa | acc_norm | 0.8101 | 0.8107 | 0.0091 | 0.0006 |
| lambada | ppl | 3.0142 | 3.0152 | 0.0552 | 0.001 |
| lambada | acc | 0.7464 | 0.7466 | 0.0061 | 0.0002 |
| winogrande | acc | 0.7174 | 0.7245 | 0.0125 | 0.0071 |
对于 BLOOM-176
| 基准 | - | - | - | - | 差异 - 值 |
|---|---|---|---|---|---|
| 名称 | 指标 | 值 - int8 | 值 - bf16 | 标准误差 - bf16 | - |
| hellaswag | acc_norm | 0.7274 | 0.7303 | 0.0044 | 0.0029 |
| hellaswag | acc | 0.5563 | 0.5584 | 0.005 | 0.0021 |
| piqa | acc | 0.7835 | 0.7884 | 0.0095 | 0.0049 |
| piqa | acc_norm | 0.7922 | 0.7911 | 0.0095 | 0.0011 |
| lambada | ppl | 3.9191 | 3.931 | 0.0846 | 0.0119 |
| lambada | acc | 0.6808 | 0.6718 | 0.0065 | 0.009 |
| winogrande | acc | 0.7048 | 0.7048 | 0.0128 | 0 |
我们确实观察到这些模型没有性能下降,因为指标的绝对差异都低于标准误差(BLOOM-int8 除外,它在 lambada 上略优于原生模型)。有关与最先进方法进行更详细的性能评估,请参阅论文!
它比原生模型更快吗?
LLM.int8() 方法的主要目的是在不降低性能的情况下使大型模型更易于访问。但如果该方法速度很慢,则用处不大。因此,我们对多个模型的生成速度进行了基准测试。我们发现使用 LLM.int8() 的 BLOOM-176B 比 fp16 版本慢约 15% 到 23%——这仍然是相当可以接受的。我们发现对于较小的模型,如 T5-3B 和 T5-11B,减速更大。我们努力加快这些小型模型的速度。一天之内,我们将 T5-3B 的每令牌推理时间从 312 毫秒提高到 173 毫秒,将 T5-11B 的每令牌推理时间从 45 毫秒提高到 25 毫秒。此外,已经发现了问题,LLM.int8() 在即将发布的版本中可能会对小型模型更快。目前,当前数字如下表所示。
| 精度 | 参数数量 | 硬件 | 批量大小为 1 时每令牌的时间(毫秒) | 批量大小为 8 时每令牌的时间(毫秒) | 批量大小为 32 时每令牌的时间(毫秒) |
|---|---|---|---|---|---|
| bf16 | 176B | 8xA100 80GB | 239 | 32 | 9.9 |
| int8 | 176B | 4xA100 80GB | 282 | 37.5 | 10.2 |
| bf16 | 176B | 14xA100 40GB | 285 | 36.5 | 10.4 |
| int8 | 176B | 5xA100 40GB | 367 | 46.4 | oom |
| fp16 | 11B | 2xT4 15GB | 11.7 | 1.7 | 0.5 |
| int8 | 11B | 1xT4 15GB | 43.5 | 5.3 | 1.3 |
| fp32 | 3B | 2xT4 15GB | 45 | 7.2 | 3.1 |
| int8 | 3B | 1xT4 15GB | 312 | 39.1 | 10.2 |
这 3 个模型是 BLOOM-176B、T5-11B 和 T5-3B。
Hugging Face transformers 集成细微之处
接下来让我们讨论 Hugging Face transformers 集成的具体细节。让我们看看用法以及您在设置时可能遇到的常见问题。
用法
本博客文章中描述的所有神奇功能都由名为 Linear8bitLt 的模块负责,您可以轻松地从 bitsandbytes 库中导入它。它派生自经典的 torch.nn 模块,可以轻松地使用下面的代码在您的架构中使用和部署。
以下是以下用例的分步示例:假设您想使用 bitsandbytes 将一个小模型转换为 int8。
- 首先,我们需要正确的导入!
import torch
import torch.nn as nn
import bitsandbytes as bnb
from bnb.nn import Linear8bitLt
- 然后您可以定义自己的模型。请注意,您可以将任何精度的检查点或模型转换为 8 位(FP16、BF16 或 FP32),但目前,模型的输入必须是 FP16 才能使我们的 Int8 模块工作。因此,我们在这里将模型视为 fp16 模型。
fp16_model = nn.Sequential(
nn.Linear(64, 64),
nn.Linear(64, 64)
)
- 假设您已经在您最喜欢的数据集和任务上训练了您的模型!现在是时候保存模型了
[... train the model ...]
torch.save(fp16_model.state_dict(), "model.pt")
- 现在您的
state_dict已保存,让我们定义一个 int8 模型
int8_model = nn.Sequential(
Linear8bitLt(64, 64, has_fp16_weights=False),
Linear8bitLt(64, 64, has_fp16_weights=False)
)
这里非常重要的是要添加 has_fp16_weights 标志。默认情况下,这设置为 True,用于以混合 Int8/FP16 精度进行训练。但是,我们感兴趣的是内存高效推理,为此我们需要使用 has_fp16_weights=False。
- 现在是时候以 8 位加载模型了!
int8_model.load_state_dict(torch.load("model.pt"))
int8_model = int8_model.to(0) # Quantization happens here
请注意,量化步骤是在模型设置到 GPU 上后第二行完成的。如果您在调用 .to 函数之前打印 int8_model[0].weight,您会得到
int8_model[0].weight
Parameter containing:
tensor([[ 0.0031, -0.0438, 0.0494, ..., -0.0046, -0.0410, 0.0436],
[-0.1013, 0.0394, 0.0787, ..., 0.0986, 0.0595, 0.0162],
[-0.0859, -0.1227, -0.1209, ..., 0.1158, 0.0186, -0.0530],
...,
[ 0.0804, 0.0725, 0.0638, ..., -0.0487, -0.0524, -0.1076],
[-0.0200, -0.0406, 0.0663, ..., 0.0123, 0.0551, -0.0121],
[-0.0041, 0.0865, -0.0013, ..., -0.0427, -0.0764, 0.1189]],
dtype=torch.float16)
而在调用第二行之后打印,您会得到
int8_model[0].weight
Parameter containing:
tensor([[ 3, -47, 54, ..., -5, -44, 47],
[-104, 40, 81, ..., 101, 61, 17],
[ -89, -127, -125, ..., 120, 19, -55],
...,
[ 82, 74, 65, ..., -49, -53, -109],
[ -21, -42, 68, ..., 13, 57, -12],
[ -4, 88, -1, ..., -43, -78, 121]],
device='cuda:0', dtype=torch.int8, requires_grad=True)
正如我们在前几节解释量化时所看到的,权重值是“截断”的。此外,值似乎分布在 [-127, 127] 之间。您可能还会想,如何检索 FP16 权重以执行 fp16 中的异常值 MatMul?您只需执行以下操作
(int8_model[0].weight.CB * int8_model[0].weight.SCB) / 127
你会得到
tensor([[ 0.0028, -0.0459, 0.0522, ..., -0.0049, -0.0428, 0.0462],
[-0.0960, 0.0391, 0.0782, ..., 0.0994, 0.0593, 0.0167],
[-0.0822, -0.1240, -0.1207, ..., 0.1181, 0.0185, -0.0541],
...,
[ 0.0757, 0.0723, 0.0628, ..., -0.0482, -0.0516, -0.1072],
[-0.0194, -0.0410, 0.0657, ..., 0.0128, 0.0554, -0.0118],
[-0.0037, 0.0859, -0.0010, ..., -0.0423, -0.0759, 0.1190]],
device='cuda:0')
这与原始的 FP16 值(上方打印的两个值)足够接近!
- 现在您可以安全地使用您的模型进行推理,确保您的输入在正确的 GPU 上且为 FP16
input_ = torch.randn((1, 64), dtype=torch.float16)
hidden_states = int8_model(input_.to(torch.device('cuda', 0)))
查看 示例脚本 获取完整的最小代码!
另外,您应该注意,这些模块与 nn.Linear 模块略有不同,因为它们的参数来自 bnb.nn.Int8Params 类而不是 nn.Parameter 类。您稍后会发现,这在我们的旅程中提出了额外的障碍!
现在是时候了解如何将其集成到 transformers 库中了!
accelerate 是您所需要的一切
在处理大型模型时,accelerate 库包含许多有用的实用工具。init_empty_weights 方法特别有用,因为任何模型,无论大小,都可以使用此方法作为上下文管理器进行初始化,而无需为模型权重分配任何内存。
import torch.nn as nn
from accelerate import init_empty_weights
with init_empty_weights():
model = nn.Sequential([nn.Linear(100000, 100000) for _ in range(1000)]) # This will take ~0 RAM!
初始化后的模型将放置在 PyTorch 的 meta 设备上,这是一种底层机制,用于表示形状和数据类型而无需分配内存。这多酷啊!
最初,此函数在 .from_pretrained 函数内部被调用,并将所有参数覆盖为 torch.nn.Parameter。这不符合我们的要求,因为我们希望在 Linear8bitLt 模块的案例中保留 Int8Params 类,如上所述。我们设法在 以下 PR 中解决了这个问题,该 PR 修改了
module._parameters[name] = nn.Parameter(module._parameters[name].to(torch.device("meta")))
到
param_cls = type(module._parameters[name])
kwargs = module._parameters[name].__dict__
module._parameters[name] = param_cls(module._parameters[name].to(torch.device("meta")), **kwargs)
现在这个问题已经解决了,我们可以轻松利用这个上下文管理器,并通过自定义函数替换 meta 设备上初始化的所有 nn.Linear 模块为 bnb.nn.Linear8bitLt,而无需任何内存开销!
def replace_8bit_linear(model, threshold=6.0, module_to_not_convert="lm_head"):
for name, module in model.named_children():
if len(list(module.children())) > 0:
replace_8bit_linear(module, threshold, module_to_not_convert)
if isinstance(module, nn.Linear) and name != module_to_not_convert:
with init_empty_weights():
model._modules[name] = bnb.nn.Linear8bitLt(
module.in_features,
module.out_features,
module.bias is not None,
has_fp16_weights=False,
threshold=threshold,
)
return model
此函数递归地将给定模型在 meta 设备上初始化的所有 nn.Linear 层替换为 Linear8bitLt 模块。属性 has_fp16_weights 必须设置为 False,以便直接加载 int8 中的权重以及量化统计信息。
我们还放弃了对某些模块(这里是 lm_head)的替换,因为我们希望它们保持其原生精度,以获得更精确和稳定的结果。
但是还没结束!上述函数在 init_empty_weights 上下文管理器下执行,这意味着新模型仍将位于 meta 设备中。对于在此上下文管理器下初始化的模型,accelerate 将手动加载每个模块的参数并将其移动到正确的设备。在 bitsandbytes 中,设置 Linear8bitLt 模块的设备是一个关键步骤(如果您好奇,可以查看 这里的代码片段),正如我们在玩具脚本中看到的那样。
这里,当两次调用时,量化步骤会失败。我们不得不实现 accelerate 的 set_module_tensor_to_device 函数(称为 set_module_8bit_tensor_to_device),以确保我们不会两次调用它。让我们在下面详细讨论这个问题!
使用 accelerate 设置设备时要非常小心
在这里,我们与 accelerate 库玩了一场非常微妙的平衡游戏!一旦您加载模型并将其设置到正确的设备上,有时您仍然需要调用 set_module_tensor_to_device 来将模型与钩子一起分派到所有设备。这是在 accelerate 的 dispatch_model 函数内部完成的,这可能涉及多次调用 .to,这是我们想要避免的。为了实现我们的目标,需要两个拉取请求!最初的 PR 此处 提出,但此 PR 成功修复了所有问题!
总结
因此,最终的方案是
- 在
meta设备上使用正确的模块初始化模型 - 逐个将参数设置到正确的 GPU 设备上,并确保不要重复此过程!
- 将新的关键字参数放置在正确的位置,并添加一些不错的文档
- 添加非常详尽的测试!查看我们的测试此处了解更多详情。这听起来很简单,但我们一起经历了许多艰难的调试会话,通常涉及 CUDA 内核!
总而言之,这次整合之旅非常有趣;从深入研究和对不同库进行一些“手术”到协调一切并使其正常工作!
现在是时候了解如何从这次集成中受益以及如何成功地在 transformers 中使用它了!
如何在 transformers 中使用
硬件要求
CPU 不支持 8 位张量核心。bitsandbytes 可以在支持 8 位张量核心的硬件上运行,例如 Turing 和 Ampere GPU(RTX 20s、RTX 30s、A40-A100、T4+)。例如,Google Colab GPU 通常是 NVIDIA T4 GPU,它们的最新一代 GPU 支持 8 位张量核心。我们的演示基于 Google Colab,请在下面查看!
安装
只需使用以下命令安装最新版本的库(确保您使用的是 python>=3.8),然后运行以下命令进行尝试
pip install accelerate
pip install bitsandbytes
pip install git+https://github.com/huggingface/transformers.git
示例演示 - 在 Google Colab 上运行 T5 11b
查看在 BLOOM-3B 模型上运行 8 位模型的 Google Colab 演示!
这是运行 T5-11B 的演示。T5-11B 模型检查点为 FP32,占用 42GB 内存,不适合在 Google Colab 上运行。使用我们的 8 位模块,它仅占用 11GB,轻松运行
或者这是 BLOOM-3B 的演示
改进范围
在我们看来,这种方法极大地提高了对大型模型的访问能力。在不降低性能的情况下,它使计算能力较低的用户能够访问以前无法访问的模型。我们发现了一些未来可以改进的领域,以使这种方法对大型模型更好!
小型模型的更快的推理速度
正如我们在基准测试部分所看到的,我们可以将小型模型(<=6B 参数)的运行时速度提高近 2 倍。然而,尽管 BLOOM-176B 等大型模型的推理速度稳定,但小型模型仍有改进空间。我们已经确定了问题,并且很可能恢复与 fp16 相同的性能,或者获得小幅加速。您将在未来几周内看到这些更改集成。
支持 Kepler GPU(GTX 1080 等)
虽然我们支持过去四年内的所有 GPU,但一些旧的 GPU(如 GTX 1080)仍在使用。虽然这些 GPU 没有 Int8 张量核心,但它们确实有 Int8 向量单元(一种“弱”张量核心)。因此,这些 GPU 也可以体验到 Int8 加速。然而,它需要一个完全不同的软件堆栈才能实现快速推理。尽管我们确实计划集成对 Kepler GPU 的支持,以使 LLM.int8() 功能更广泛地可用,但由于其复杂性,实现这一点将需要一些时间。
在 Hub 上保存 8 位状态字典
目前,8 位状态字典无法在推送到 Hub 后直接加载到 8 位模型中。这是因为模型计算的统计数据(记住 weight.CB 和 weight.SCB)目前未存储或未在状态字典中考虑,并且 Linear8bitLt 模块尚不支持此功能。我们认为能够保存并推送到 Hub 可能会有助于提高可访问性。
CPU 支持
如本博客文章开头所述,CPU 设备不支持 8 位核心。但是,我们能否克服这一点?在 CPU 上运行此模块也将显著提高可用性和可访问性。
在其他模态上进行扩展
目前,语言模型在大型模型中占据主导地位。随着这些模型在未来几年变得更易于访问,将此方法应用于大型视觉、音频和多模态模型可能是一个有趣的选择,以提高可访问性。
鸣谢
衷心感谢以下为提高文章可读性以及为 transformers 的集成过程做出贡献的人士(按字母顺序排列):JustHeuristic (Yozh)、Michael Benayoun、Stas Bekman、Steven Liu、Sylvain Gugger、Tim Dettmers