上下文并行（Context Parallelism）

如您所见，大型语言模型正在席卷全球，每个人都在使用它，它能够将人类的生产力和智能提升到我们意想不到的水平。

您可以与LLM聊天，几乎可以做任何想做的事情，从扮演婴儿到询问您不理解的研究论文的反馈循环。

ChatGPT于2022年11月30日发布时，它只支持最大4096个上下文长度或4096个标记，基于ChatGPT分词器，1个标记平均2个单词，所以是8192个单词。让我们用下面的聊天气泡作为例子，绿色聊天气泡是用户，灰色聊天气泡是助手，

在此示例中，我们假设1个标记等于1个单词，所以单词是['hello', 'hi!', 'How', 'can', 'I', 'help', 'you?', 'do', 'u', 'know', 'about', 'Toyota?', 'Of', 'course', 'I', 'know', 'about', 'Toyota!']，总共18个单词或18个标记。因此，当LLM支持4096个上下文长度时，它可以支持总共4096个标记的多轮对话。

如今，LLM可以支持百万级别的上下文长度，Google的Gemini可以支持高达1百万个标记的上下文长度，您可以给它一整本书或一篇研究论文，然后问任何您想问的问题！

在不到2年的时间里，我们从4096个上下文长度发展到1百万个上下文长度！

LLM如何能够从仅4096个标记服务到1百万个标记？ 上下文并行！

粗略计算内存使用情况

注意力机制定义为：

$$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V\backslash text\{Attention\}(Q,\; K,\; V)\; =\; \backslash text\{softmax\}\backslash left(\backslash frac\{QK^T\}\{\backslash sqrt\{d\_k\}\}\backslash right)\; V$$

其中 Q 是查询矩阵，K 是键矩阵，V 是值矩阵。LLM 是解码器模型，所以注意力是自注意力。现在举个例子，

• QKV的隐藏大小或`d_model`为10，所以QKV的每个大小为[2, 10]，2个输入维度，10个隐藏维度。

• 输入形状为 [5, 2]，其中 5 为序列长度或 L，2 为隐藏维度或 in_d_model。

• 输入将与QKV矩阵进行矩阵乘法，

• 1. 输入[5,2] 矩阵乘 Q [2, 10] = [5, 10]
• 2. 输入[5,2] 矩阵乘 K [2, 10] = [5, 10]
• 3. 输入[5,2] 矩阵乘 V [2, 10] = [5, 10]
• 4. 之后计算注意力，

输出形状应为 [Q L, V d_model] = [5, 10]。粗略计算内存使用情况基于输出形状，

• 1. Q、K 和 V 的线性权重，每个输出为 [in_d_model, d_model]，即 3 x in_d_model x d_model。
• 2. 输入与Q、K和V进行矩阵乘法，每个输出为[L, d_model]，即3 x L x d_model。
• 3. softmax(QK^T)V，[L, d_model]，L x d_model。
• 4. 总计：(3 x in_d_model x d_model) + (3 x L x d_model) + (L x d_model) = 260。
• 7. 假设我们存储为 bfloat16，则为 260 x 2 = 520 字节。

520字节非常小，这只是一个简单的例子，但如果使用至少8B参数的LLM（如Llama 3.1）呢？

使用实际的 Llama 3.1 8B 参数

根据 HuggingFace 上的 Llama 3.1 8B 参数设置，https://huggingface.co/meta-llama/Meta-Llama-3.1-8B/blob/main/config.json，有 3 个设置对于注意力大小很重要：

• 1. 隐藏层尺寸 = 4096.
• 2. 注意力头数量 = 32.

由于Llama使用多头注意力，为了简化注意力，假设没有使用分组多头注意力（即`num_key_value_heads`），假设输入形状为[5, 4096]，5个序列长度和4096个隐藏层大小，所以在计算注意力时，

• 1. head_dim = hidden_size // num_attention_heads
• 2. Q、K、V 线性权重 [hidden_size, num_attention_heads x head_dim]，3 x hidden_size x num_attention_heads x head_dim。
• 3. 输入矩阵与 Q、K 和 V 相乘，每个输出形状为 [L, num_attention_heads x head_dim]，并重塑为 [num_attention_heads, L, head_dim]，即 3 x L x num_attention_heads x head_dim。
• 4. softmax(QK^T)V = [num_attention_heads, L, head_dim]，num_attention_heads x L x head_dim。
• 5. 总计，(3 x hidden_size x num_attention_heads x head_dim) + (3 x L x num_attention_heads x head_dim) + (num_attention_heads x L x head_dim) = 50413568。
• 6. 假设我们存储为bfloat16，则为50413568 x 2 = 100827136字节或0.100827136 GB，仍然很小。

现在，如果你有 1M 的序列长度或 1M 的上下文长度呢？用 1M 替换 L，你将得到 16434331648 字节，如果存储为 bfloat16，则为 16434331648 x 2 = 32868663296 字节，或 32.868663296 GB！

32.868663296 GB 仅用于注意力，不包括其他线性层和其他矩阵乘法运算，这太疯狂了。那如果是13B或70B参数呢？更爆炸！

上下文并行（Context Parallelism）

当我们谈论深度学习中的并行化时，它是关于如何将数据并行化到多个 GPU 中，以减少计算负担，同时减少内存消耗，或者复制副本以增加输入大小，从而加快学习过程。上下文并行化是关于如何将序列长度并行化到多个 GPU 中。假设我有 2 个 GPU，因此分区大小为 2，

所以现在每个 GPU 都可以计算自己的局部注意力，但仍然与其他局部注意力保持一致，如果你收集并组合这些局部注意力，组合后的结果应该与完全注意力几乎相同，只有超级微小的差异，并且你通过分区大小的因子节省了 GPU 内存！

如果我们把QKV分成2个GPU，Q = [Q1, Q2]，K = [K1, K2]，V = [V1, V2]，那么局部注意力就是Attention1=softmax(Q1K1^T)V1和Attention2=softmax(Q2K2^T)V2。

现在，softmax(Q1K1^T)V1 如何与 softmax(Q2K2^T)V2 相关联？ 特别是在 softmax 上，因为 softmax 需要隐藏维度上的指数和。

用于大型上下文模型的块级并行Transformer

这篇论文https://arxiv.org/pdf/2305.19370表明我们可以在多个设备上以块级方式计算注意力。

这篇论文还提到“自注意力可以以块状方式计算，而无需具体化softmax注意力矩阵”，这已经在Flash Attention: 2205.14135和Self-attention does not need o(n2) memory: 2112.05682中完成。

Flash Attention

"Flash Attention"将QKV在GPU内部划分为块，并用CUDA核编写，优化了GPU高带宽内存（HBM）和GPU片上SRAM之间的数据移动，通过直接操作CUDA接口的内存层次结构，变得更加“IO感知”。Flash Attention还通过CUDA块内部的块级方式计算注意力。

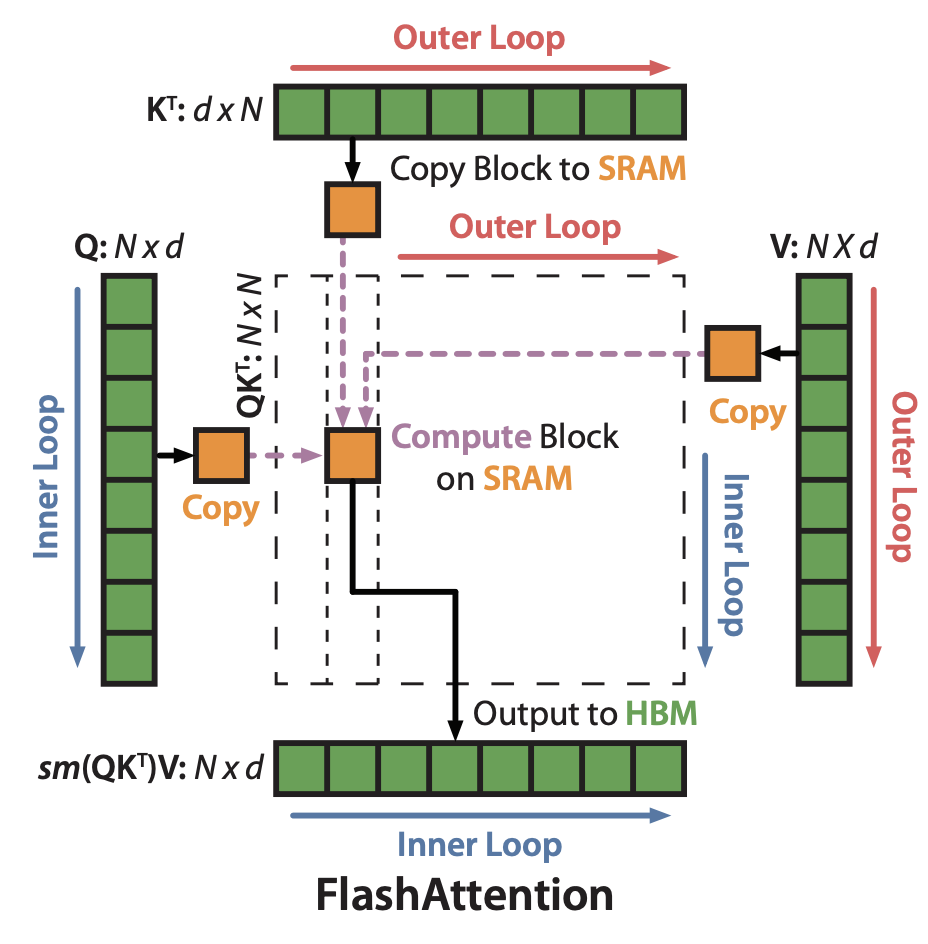
如您所见，有外层和内层循环，定义为：对每个KV块进行循环，对每个Q块进行嵌套循环，并计算局部最大值和局部注意力，然后收集局部最大值以获得全局最大值，并对每个局部注意力减去全局最大值以获得全局注意力。

自注意力不需要 o(n2) 内存

虽然自注意力不需要 o(n2) 内存: 2112.05682使用Jax编写块级计算，但其效率不如Flash Attention: 2205.14135，因为Jax处理所有内存，并且没有像Flash Attention: 2205.14135那样的“IO感知”接口。Jax中的实现，

import functools, jax, math
from jax import lax
from jax import numpy as jnp


def _query_chunk_attention(query,
                           key,
                           value,
                           key_chunk_size=4096,
                           precision=lax.Precision.HIGHEST,
                           dtype=jnp.float32):
  num_kv, num_heads, k_features = key.shape
  v_features = value.shape[-1]
  key_chunk_size = min(key_chunk_size, num_kv)
  query = query / jnp.sqrt(k_features).astype(dtype)

  @functools.partial(jax.checkpoint, prevent_cse=False)
  def summarize_chunk(query, key, value):
    attn_weights = jnp.einsum(
        'qhd,khd->qhk', query, key, precision=precision).astype(dtype)
    max_score = jnp.max(attn_weights, axis=-1, keepdims=True)
    max_score = jax.lax.stop_gradient(max_score)
    exp_weights = jnp.exp(attn_weights - max_score)
    exp_values = jnp.einsum(
        'vhf,qhv->qhf', value, exp_weights, precision=precision).astype(dtype)
    return (exp_values, exp_weights.sum(axis=-1),
            max_score.reshape((query.shape[0], num_heads)))

  def chunk_scanner(chunk_idx):
    key_chunk = lax.dynamic_slice(
        key, (chunk_idx, 0, 0),
        slice_sizes=(key_chunk_size, num_heads, k_features))
    value_chunk = lax.dynamic_slice(
        value, (chunk_idx, 0, 0),
        slice_sizes=(key_chunk_size, num_heads, v_features))
    return summarize_chunk(query, key_chunk, value_chunk)

  chunk_values, chunk_weights, chunk_max = lax.map(
      chunk_scanner, xs=jnp.arange(0, num_kv, key_chunk_size))

  global_max = jnp.max(chunk_max, axis=0, keepdims=True)
  max_diffs = jnp.exp(chunk_max - global_max)
  chunk_values *= jnp.expand_dims(max_diffs, axis=-1)
  chunk_weights *= max_diffs

  all_values = chunk_values.sum(axis=0)
  all_weights = jnp.expand_dims(chunk_weights, -1).sum(axis=0)
  return all_values / all_weights


def mefficient_attention(query,
                         key,
                         value,
                         query_chunk_size=1024,
                         precision=jax.lax.Precision.HIGHEST,
                         dtype=jnp.float32):
  num_q, num_heads, q_features = query.shape

  def chunk_scanner(chunk_idx, _):
    query_chunk = lax.dynamic_slice(
        query, (chunk_idx, 0, 0),
        slice_sizes=(min(query_chunk_size, num_q), num_heads, q_features))
    return (chunk_idx + query_chunk_size,
            _query_chunk_attention(
                query_chunk, key, value, precision=precision, dtype=dtype))

  _, res = lax.scan(
      chunk_scanner,
      init=0,
      xs=None,
      length=math.ceil(num_q / query_chunk_size))
  return res.reshape(num_q, num_heads, value.shape[-1])

但基本相同，循环Q块，循环嵌套KV块，计算局部最大值和局部注意力，收集局部最大值以获得全局最大值，然后每个局部注意力减去全局最大值以获得全局注意力。

1. 将 Q 分块，

query_chunk = lax.dynamic_slice(
        query, (chunk_idx, 0, 0),
        slice_sizes=(min(query_chunk_size, num_q), num_heads, q_features))

2. 计算 QiKj^T，

attn_weights = jnp.einsum('qhd,khd->qhk', query, key, precision=precision).astype(dtype)

3. 计算局部最大值，

max_score = jnp.max(attn_weights, axis=-1, keepdims=True)

4. 计算块级注意力，

global_max = jnp.max(chunk_max, axis=0, keepdims=True)
max_diffs = jnp.exp(chunk_max - global_max)
chunk_values *= jnp.expand_dims(max_diffs, axis=-1)
chunk_weights *= max_diffs

all_values = chunk_values.sum(axis=0)
all_weights = jnp.expand_dims(chunk_weights, -1).sum(axis=0)
all_values / all_weights

但是Flash Attention: 2205.14135和Self-attention does not need o(n2) memory:2112.05682将QKV划分成块，发生在单个GPU内部，而不是用于多GPU。

实际上，用于大上下文模型的块级并行Transformer：2305.19370直接受到自注意力不需要o(n2)内存：2112.05682的启发，但只是在多GPU层面进行。

用于大上下文模型的块级并行Transformer，第3节

在第3节中，它指出Q可以分成Bq块，KV可以分成Bkv块，与Flash Attention: 2205.14135和Self-attention does not need o(n2) memory: 2112.05682相同。

1. 对于每个查询块，块级注意力Attention(Qi, Kj, Vj)可以通过迭代所有键值块来计算，

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q_i,K,V)=\mathrm{S}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{g}(\{\exp (Q_i{K}_j^T)V_j{\}}_{j=1}^{B_{kv}})\backslash mathrm\{Attention\}(Q\_i,\; K,\; V)\; =\; \backslash mathrm\{Scaling\}(\backslash \{\backslash exp(Q\_i\; K\_j^T)V\_j\backslash \}\_\{j=1\}^\{B\_\{kv\}\})$$

2. 缩放操作根据块级最大值和全局最大值之间的差异来缩放每个块级注意力。

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q_i,K_j,V_j)=\exp (Q_i{K}_j^T-\max (Q_i{K}_j^T))\mathrm{/}\sum \exp )\backslash mathrm\{Attention\}(Q\_i,\; K\_j,\; V\_j)\; =\; \backslash exp\backslash bigl(Q\_i\; K\_j^T\; -\; \backslash max(Q\_i\; K\_j^T)\backslash bigr)\; /\; \backslash sum\; \backslash exp\backslash bigl(Q\_i\; K\_j^T\; -\; \backslash max(Q\_i\; K\_j^T)\backslash bigr)$$

$${\mathrm{m}\mathrm{a}\mathrm{x}}_i=\max (\max (Q_i{K}_1^T),\dots ,\max (Q_i{K}_B^T))\backslash mathrm\{max\}\_i\; =\; \backslash max\; \backslash bigl(\backslash max(Q\_i\; K\_1^T),\; \backslash ldots,\; \backslash max(Q\_i\; K\_B^T)\backslash bigr)$$

3. 一旦计算出块级注意力，就可以通过使用块级和全局softmax归一化常数之间的差异来缩放块级注意力，从而获得全局注意力矩阵。

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q_i,K,V)=[\exp (Q_i{K}_j^T-{\mathrm{m}\mathrm{a}\mathrm{x}}_i)\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q_i,K_j,V_j){]}_{j=1}^{B_{kv}}\backslash mathrm\{Attention\}(Q\_i,\; K,\; V)\; =\; \backslash bigl[\; \backslash exp(Q\_i\; K\_j^T\; -\; \backslash mathrm\{max\}\_i)~\backslash mathrm\{Attention\}(Q\_i,\; K\_j,\; V\_j)\; \backslash bigr]\_\{j=1\}^\{B\_\{kv\}\}$$

4. 但我认为在计算 $\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q_i,K,V)\backslash mathrm\{Attention\}(Q\_i,\; K,\; V)$ 时，有错误。

• 一. $Q_i{K}_j^{T}Q\_i\; K\_j^T$ 形状为 [L, L]，而 $\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q_i,K,V)\backslash mathrm\{Attention\}(Q\_i,\; K,\; V)$ 形状为 [L, dim]，所以我们不能做哈达玛积。
• 二、应该是 $\exp (\max (Q_i{K}_j^T)-{\mathrm{m}\mathrm{a}\mathrm{x}}_i)\backslash exp(\backslash max(Q\_i\; K\_j^T)\; -\; \backslash mathrm\{max\}\_i)$，这样形状将变成 [L]。当我们进行哈达玛乘积时，[L] o [L, dim]，PyTorch 将自动重复 [L]，[L, L, ...] 变成 [L, dim]，然后我们就可以进行 [L, dim] o [L, dim]。
• 三、实际公式应为，

$$\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q_i,K,V)=[\exp (\max (Q_i{K}_j^T)-{\mathrm{m}\mathrm{a}\mathrm{x}}_i)\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q_i,K_j,V_j){]}_{j=1}^{B_{kv}}\backslash mathrm\{Attention\}(Q\_i,\; K,\; V)\; =\; \backslash bigl[\; \backslash exp(\backslash max(Q\_i\; K\_j^T)\; -\; \backslash mathrm\{max\}\_i)~\backslash mathrm\{Attention\}(Q\_i,\; K\_j,\; V\_j)\; \backslash bigr]\_\{j=1\}^\{B\_\{kv\}\}$$

用于获得 $\mathrm{A}\mathrm{t}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(Q_i,K,V)\backslash mathrm\{Attention\}(Q\_i,\; K,\; V)$ 的可视化效果如下，

使用循环的PyTorch代码

为了测试它是否有效，我们必须通过全注意力与块级注意力进行比较，然后将全注意力在第一个分区大小上与第一个块级注意力进行比较，

import torch
import torch.nn.functional as F

Q = torch.randn(100, 128).cuda().to(torch.bfloat16)
K = torch.randn(100, 128).cuda().to(torch.bfloat16)
V = torch.randn(100, 128).cuda().to(torch.bfloat16)

full_attention = torch.matmul(F.softmax(torch.matmul(Q, K.T), dim = -1), V)

chunk_size = 2
Q_blocks = torch.chunk(Q, chunk_size)
K_blocks = torch.chunk(K, chunk_size)
V_blocks = torch.chunk(V, chunk_size)

Q_block = Q_blocks[0]
block_attentions = []
block_maxes = []

for K_block, V_block in zip(K_blocks, V_blocks):
    # Compute attention scores
    scores = torch.matmul(Q_block, K_block.T)

    # Compute block-wise max
    block_max = scores.max(dim=-1, keepdim=True)[0]
    block_maxes.append(block_max)

    # Compute block-wise attention
    block_attention = torch.matmul(F.softmax(scores - block_max, dim=-1), V_block)
    block_attentions.append(block_attention)

# Compute global max
global_max = torch.max(torch.cat(block_maxes, dim=-1), dim=-1, keepdim=True)[0]

# Scale and combine block attentions
scaled_attentions = [
    torch.exp(block_max - global_max) * block_attention
    for block_max, block_attention in zip(block_maxes, block_attentions)
]

output = sum(scaled_attentions)

用于精确匹配符号

(torch.sign(full_attention[:output.shape[0]]) == torch.sign(output)).float().mean()

tensor(0.9958, device='cuda:0')

检查 argmax(-1) 的差异

print(full_attention[:output.shape[0]].argmax(-1), output.argmax(-1))

tensor([122,  84,  27,  20,  98,  60,  36,  65,  39,  48,  31,  91,  48,  69,
         80,  98,  59, 121,   0,  24,  42,  67,  76,  58,  36,  34,  79,   1,
         57,  99,   9,  47,  77, 110,   9,   9, 119,   9,  34,  27,   6,  37,
        104, 121, 103, 123,   0,  56,  67, 104], device='cuda:0') 

tensor([122,  84,  27,  20,  98,  60,  36,  65,  39,  48,  31,  91,  48,  69,
         80,  98,  59, 121,   0,  24,  42,  39,  76,  58,  36,  34,  79,   1,
         57,  40,   9,  47,  77, 110,   9,   9, 119,   9,  34,  27,   6,  37,
        104, 121, 103, 123,   0,  56,  67, 104], device='cuda:0')

您可以继续为Q块或Bq块运行。 如您所见，这种块级与自注意力不需要 o(n2) 内存：2112.05682完全相同，只是用PyTorch实现。

使用PyTorch分布式

现在我们必须使用Torch Elastic Distributed将循环执行转换为并行执行。对我来说，如果你想进行并行执行，首先你必须使用循环执行进行测试，如果它有效，就将其转换为并行执行。

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributed as dist
import os

def main():
    world_size = torch.cuda.device_count()
    local_rank = int(os.environ["LOCAL_RANK"])
    device = f'cuda:{local_rank}'
    dist.init_process_group(backend='nccl')

    Q_block = torch.randn(50, 128).cuda(device=device).to(torch.bfloat16)
    K = torch.randn(50, 128).cuda(device=device).to(torch.bfloat16)
    V = torch.randn(50, 128).cuda(device=device).to(torch.bfloat16)

    block_attentions = []
    block_maxes = []

    for i in range(world_size):
        if i == local_rank:
            dist.broadcast(K, src=i)
            dist.broadcast(V, src=i)

            K_block = K
            V_block = V
        else:
            K_block = torch.empty_like(K)
            V_block = torch.empty_like(V)

            dist.broadcast(K_block, src=i)
            dist.broadcast(V_block, src=i)
        
        scores = torch.matmul(Q_block, K_block.T)
        block_max = scores.max(dim=-1, keepdim=True)[0]
        block_maxes.append(block_max)
        block_attention = torch.matmul(F.softmax(scores - block_max, dim=-1), V_block)
        block_attentions.append(block_attention)
    
    global_max = torch.max(torch.cat(block_maxes, dim=-1), dim=-1, keepdim=True)[0]

    scaled_attentions = [
        torch.exp(block_max - global_max) * block_attention
        for block_max, block_attention in zip(block_maxes, block_attentions)
    ]

    output = sum(scaled_attentions)
    print(local_rank, len(block_maxes), output.shape)

if __name__ == "__main__":
    main()

将其保存为 context-parallelism.py，此示例需要至少 2 个 GPU，并使用 torchrun 执行：

torchrun \
--nproc-per-node=2 \
context-parallelism.py

0 2 torch.Size([50, 128])
1 2 torch.Size([50, 128])

每个GPU都能得到预期的形状[50, 128]，所以数据流是这样的：

1. 当我们进行上下文并行时，每个QKV块都已为每个GPU初始化，而不是在GPU 0之后再分散到N个GPU，因为GPU 0本身没有足够的内存来分块并分散到N个GPU。
2. 我们根据世界大小循环，如果我们有2个GPU，那么世界大小就是2。如果，

• 一. 如果i等于当前设备，即`i == local_rank`，我们必须将KV块广播到其他GPU。
• 二. 如果i不等于当前设备，则表示本地GPU必须从其他GPU接收KV块。
• 三、计算max(QiKj^T)并将其存储在block_maxes中。
• 四、计算softmax(QiKj^T - max(QiKj^T))Vj并将其存储在block_attentions中。

3. 从 block_maxes 计算 global_max。
4. 我们迭代来自zip(block_maxes, block_attentions)的每个块，

• i. 计算 exp(block_max - global_max) * block_attention 并存储在 scaled_attentions 中。

5. 将 scaled_attentions 求和以获得本地 GPU 上的块级注意力。

6. 数据流如下，

改进

来自同一作者的Ring Attention: 2310.01889通过简单地减少节点间的通信来改进这种块状注意力。

最近还有一篇Tree Attention: 2408.04093，通过在树状层次结构上聚合max(KV.T)来改进Ring Attention。