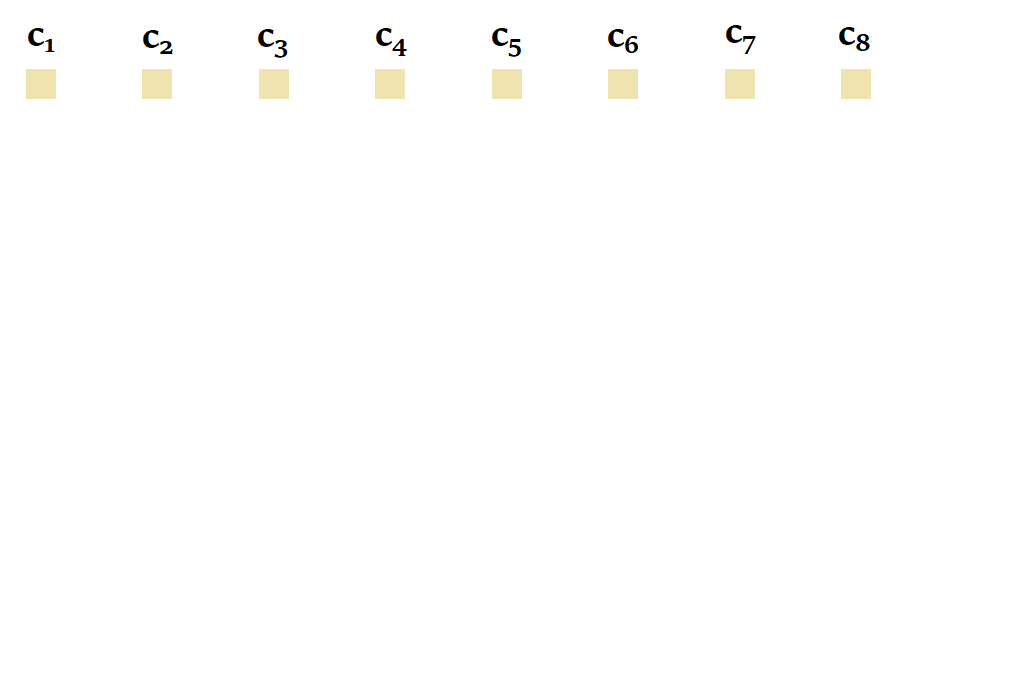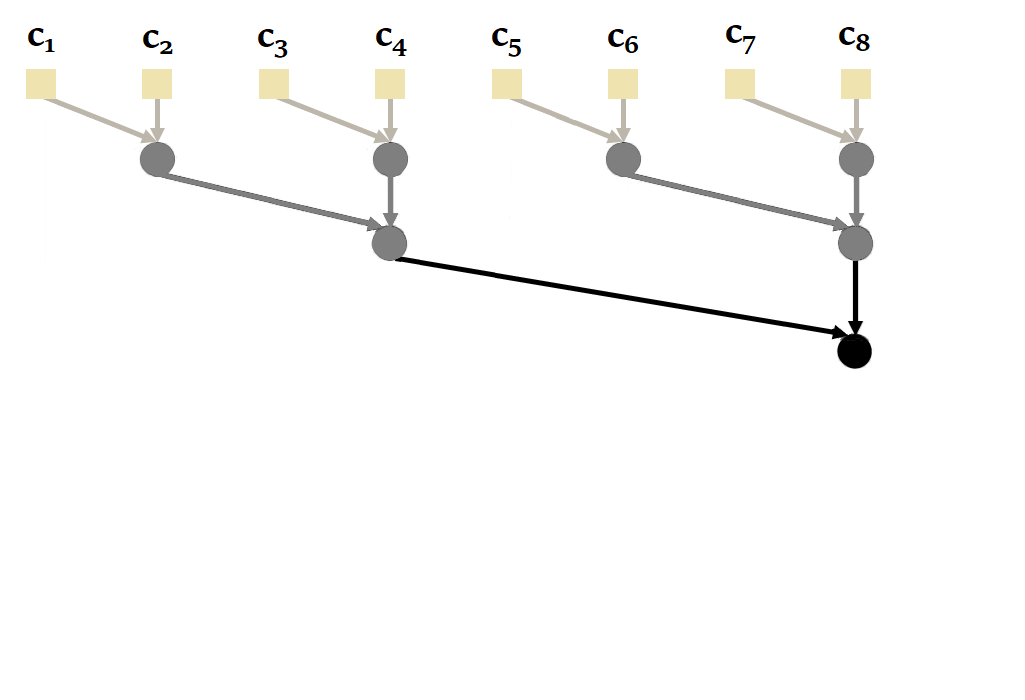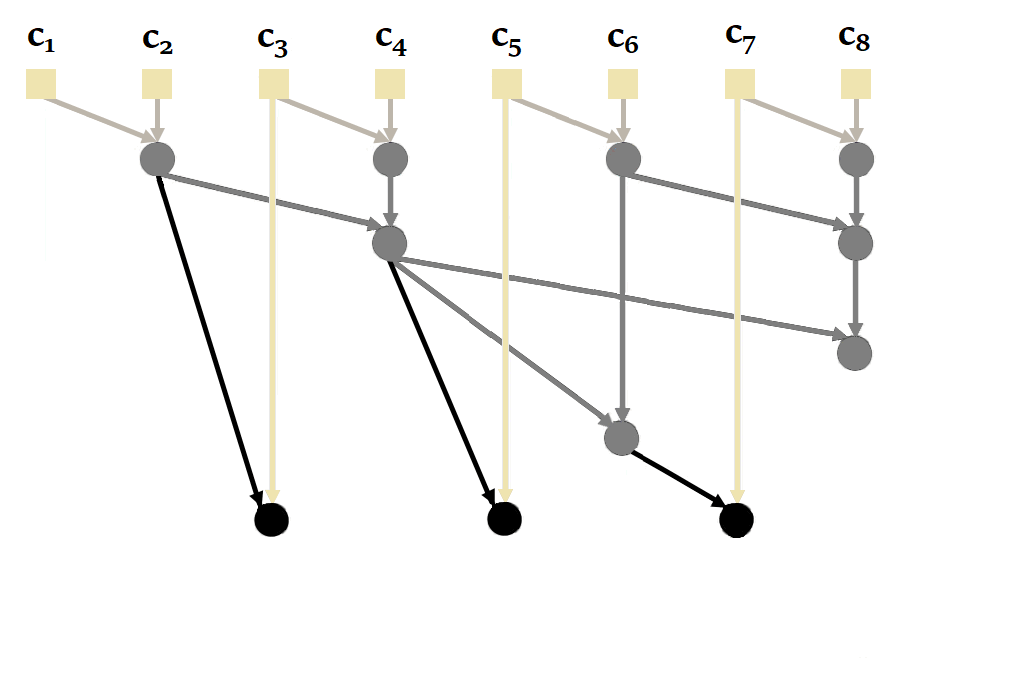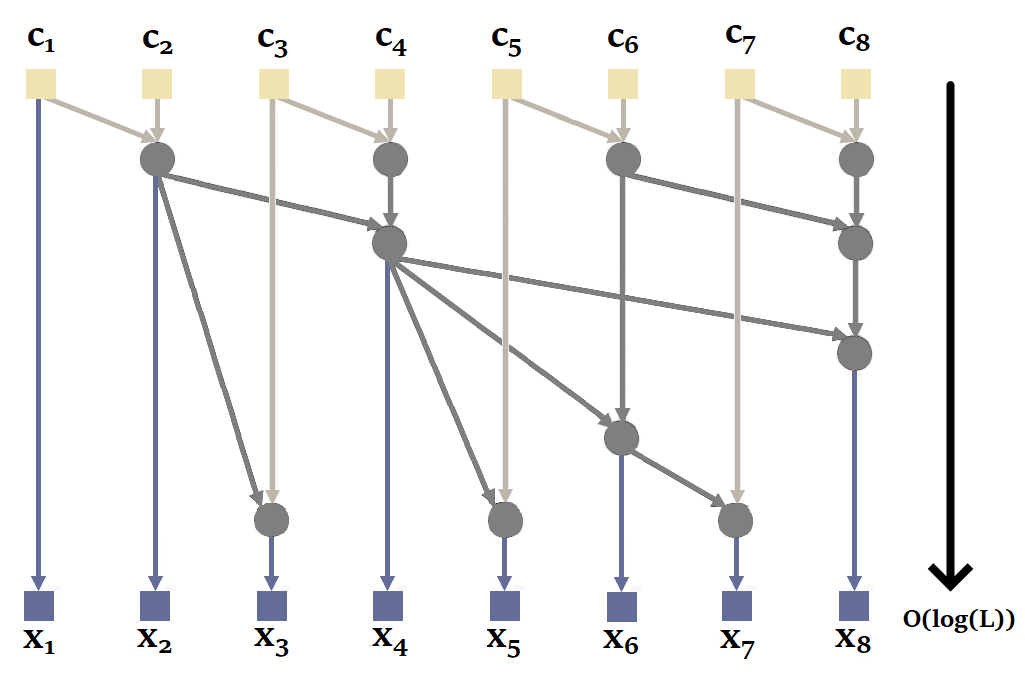2022 年状态空间模型 (SSM) 历史
法文版本可在我的博客 上找到。
在上一篇文章 中,我们使用一个连续时间系统定义了“状态空间模型”(SSM)。我们将其离散化,以展示其递归和卷积视图。这里的兴趣在于能够以卷积方式训练模型,然后对非常长的序列进行递归推理。
这一愿景由 Albert GU 在他 2021 年发表的论文LSSL 和S4 中提出。S4 相当于 Transformer 的“注意力即你所需”。HiPPO 矩阵。
理论模型
在本节中,我们将回顾 S4 架构改进背后的理论工作。然后,在另一个部分,我们将探讨其在不同任务(音频、视觉等)中的具体应用。
S4 V2
2022 年 3 月 4 日,S4 的作者更新了他们的论文,其中包含了一节关于 HiPPO 矩阵重要性的内容(参见论文最新版本第 4.4 节)。
图 2:《S4 论文》图 3,在 CIFAR-10 验证集上的准确率
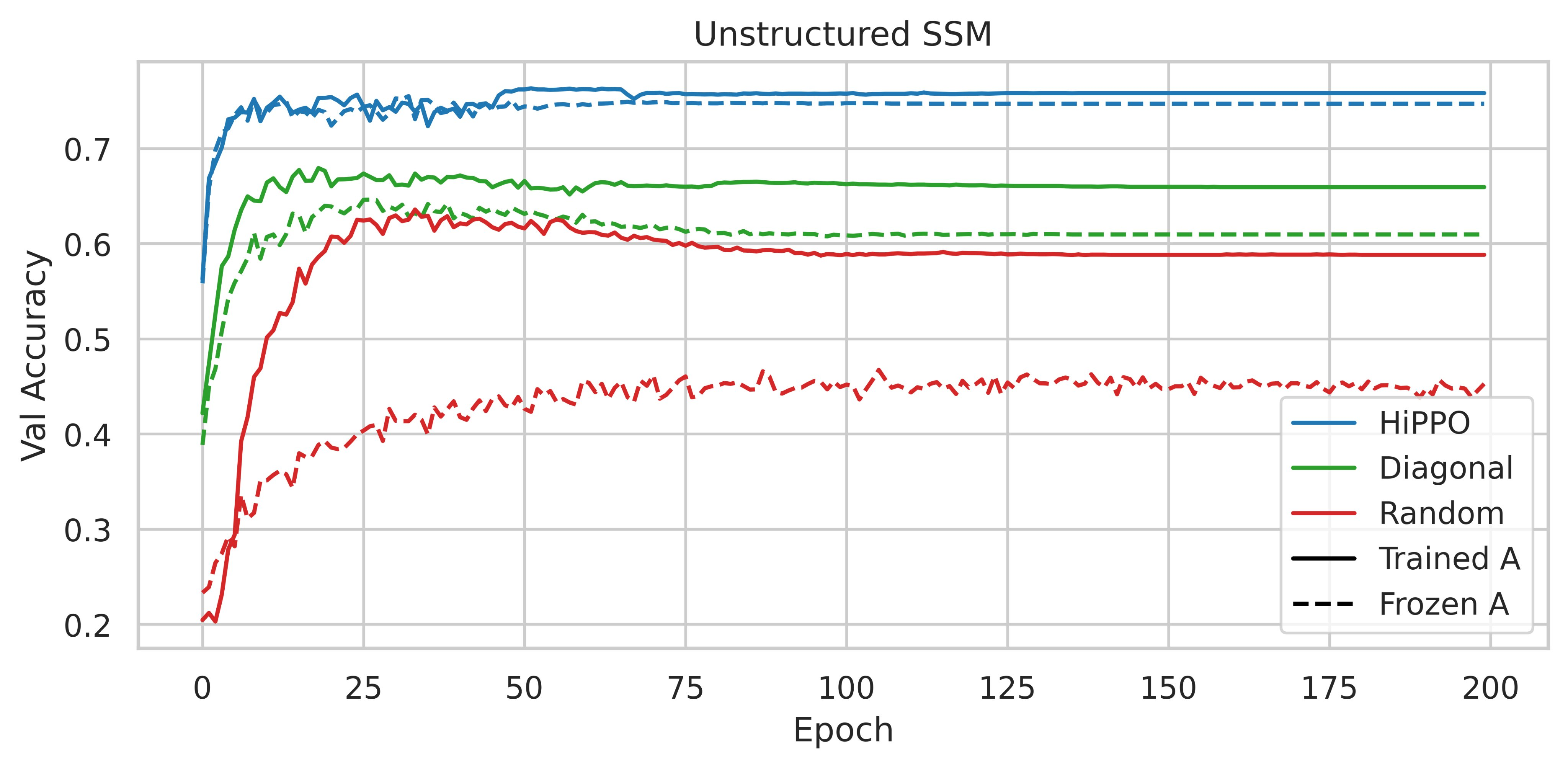
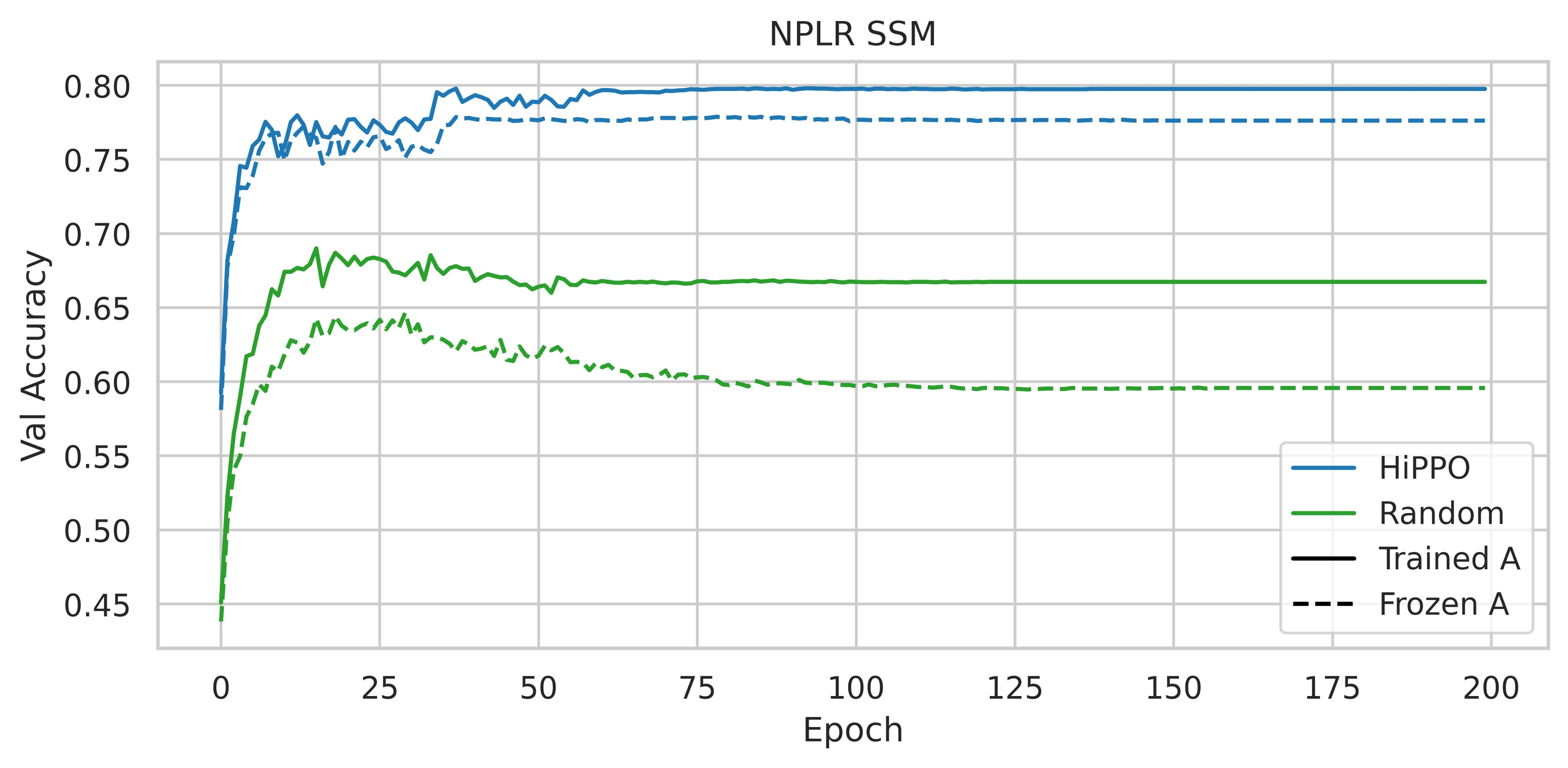
因此,HiPPO 的使用很重要。获得的性能是否归因于其特定的内在品质,或者任何低秩正规矩阵 (NPLR) 是否就足够了?
图 3:《S4 论文》图 4,在 CIFAR-10 验证集上使用不同初始化和参数化的准确率
用 HiPPO 初始化 NPLR 矩阵可以显著提高性能。因此,根据这些实验,HiPPO 矩阵对于获得高性能模型至关重要。
S4 的作者进一步发展了他们的工作,并于 2022 年 6 月 24 日在论文《如何训练你的 HiPPO》 中进行了介绍。这是一篇超过 39 页的极其详细的论文。
在这篇论文中,作者将 MSS 更直观地解释为卷积模型,其中卷积核是特定基函数的线性组合,从而引出了几种泛化和新方法。A A 短时傅里叶变换 和局部卷积(即标准 ConvNet)。这个 SSM 还可以编码最先进的函数来解决经典的记忆任务。
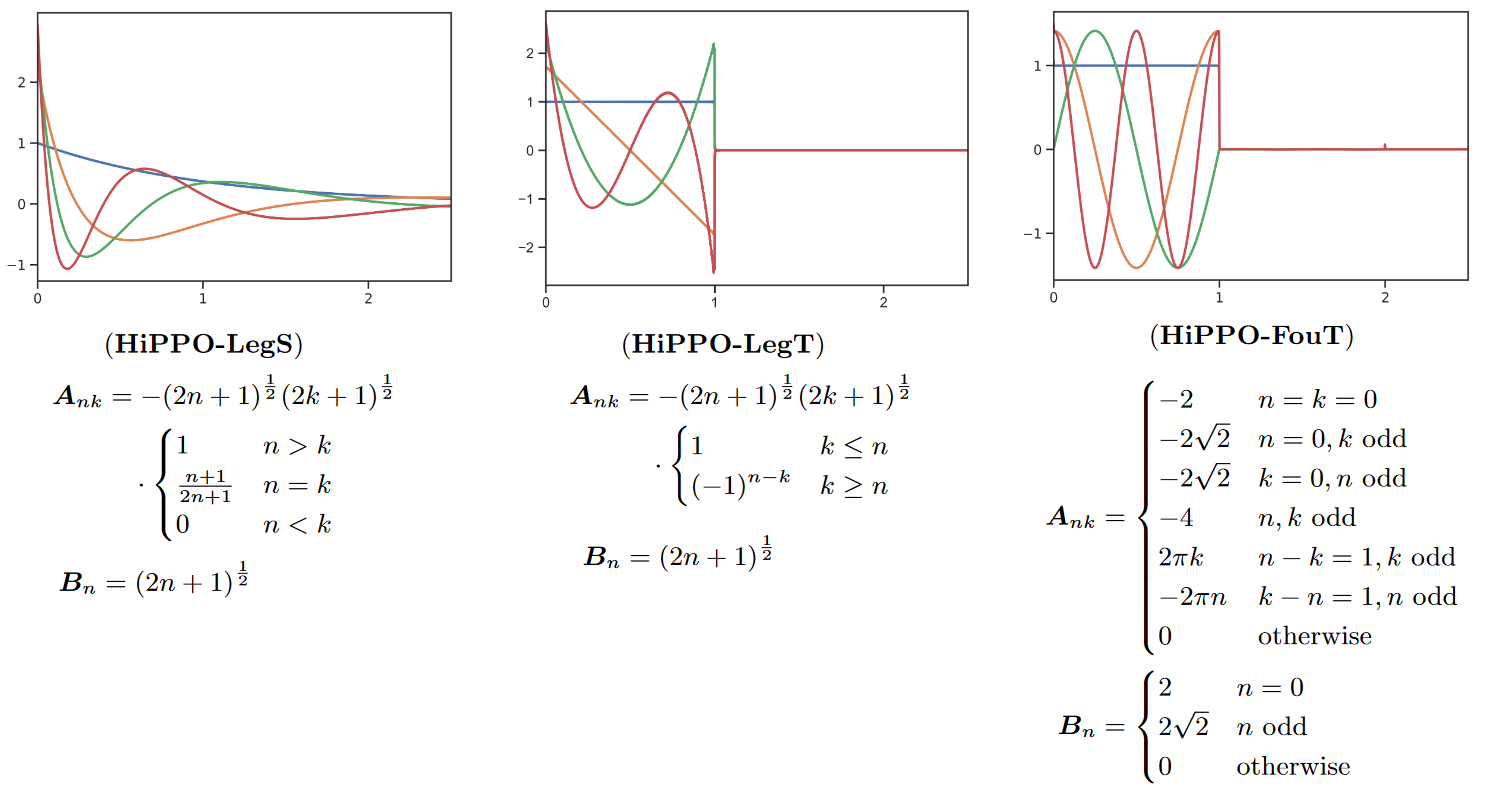
图 4:不同的 HiPPO 变体
颜色代表每种方法的前 4 个基函数K n ( t K n ( t K n ( t K n ( t
此外,作者还研究了时间步长∆ ∆ ∆ ∆
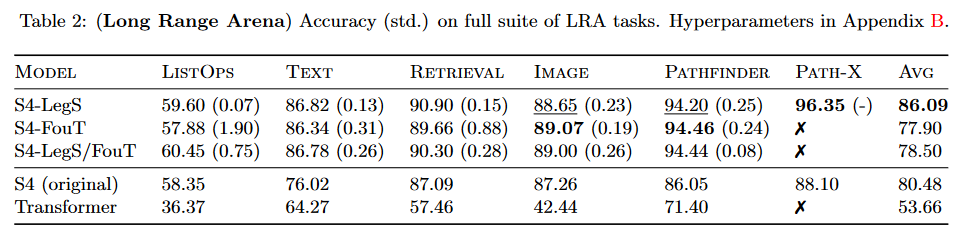
所进行的工作将 S4 在 TAY、DEHGHANI 等人(2020 年)的基准LRA 上的结果提高了 5.5 个点以上。
图 5:S4 V2 基准测试结果
本文所产生的模型在文献中通常被称为“S4 V2”或“S4 更新版”,与“原始 S4”或“S4 V1”相对。
DSS:对角线状态空间
2022 年 3 月 27 日,Ankit GUPTA 在其论文《对角线状态空间与结构化状态空间同样有效》 中介绍了“对角线状态空间”(DSS)。A A
然而,让我们探讨一下本文中包含的一些复杂性/局限性。列出它们将有助于我们理解以下方法(旨在进一步简化)的贡献。
1. 离散化
x ′ = A x + B u y = C x x ′ y = A x + B u = C x
然而,它使用不同的离散化来获得卷积和递归视图,即零阶保持 (ZOH) 离散化,而不是双线性离散化,后者假设采样信号在每个采样点之间是恒定的。A A B B C C
离散化
双线性
ZOH
递归
A ˉ = ( I − Δ 2 A ) − 1 ( I + Δ 2 A A ˉ = ( I − 2 Δ A ) − 1 ( I + 2 Δ A B ˉ = ( I − Δ 2 A ) − 1 Δ B B ˉ = ( I − 2 Δ A ) − 1 Δ B C ˉ = C C ˉ = C A ˉ = e A Δ A ˉ = e A Δ B ˉ = ( A ˉ − I ) A − 1 B B ˉ = ( A ˉ − I ) A − 1 B C ˉ = C C ˉ = C
卷积
K ˉ k = ( C ˉ B ˉ , C ˉ A ˉ B ˉ , … , C ˉ A ˉ k B ˉ K ˉ k = ( C ˉ B ˉ , C ˉ A ˉ B ˉ , … , C ˉ A ˉ k B ˉ K ˉ = ( C e A ⋅ k Δ ( e A Δ − I ) A − 1 B ) 0 ≤ k < L K ˉ = ( C e A ⋅ k Δ ( e A Δ − I ) A − 1 B ) 0 ≤ k < L
对于 ZOH,经过计算,我们得到y k = ∑ j = 0 k C ˉ A ˉ j B ˉ ⋅ u k − j = ∑ j = 0 k K ˉ j ⋅ u k − j y k = ∑ j = 0 k C ˉ A ˉ j B ˉ ⋅ u k − j = ∑ j = 0 k K ˉ j ⋅ u k − j
然后,通过快速傅里叶变换 (FFT) 在O ( L l o g ( L ) O ( L l o g ( L ) u u K ˉ K ˉ y y L L L − 1 L − 1
2. DSSsoftmax 和 DSSexp
简短版
GUPTA 提出了一个方案,以获得与 S4 具有相同表达能力的 DSS,从而产生了两种不同的 DSS:DSSexp 和 DSSsoftmax。有关它们的信息总结在下表中
方法
DSSexp
DSSsoftmax
卷积视图
K = K ˉ Δ , L ( Λ , I 1 ≤ i ≤ N , w ~ ) K = K ˉ Δ , L ( Λ , I 1 ≤ i ≤ N , w ) = w ~ ⋅ Λ − 1 ( e Λ Δ − I ) ⋅ elementwise-exp ( P ) = w ⋅ Λ − 1 ( e ΛΔ − I ) ⋅ elementwise-exp ( P ) K = K ˉ Δ , L ( Λ , ( ( e L λ i Δ − 1 ) − 1 ) 1 ≤ i ≤ N , w ) K = K ˉ Δ , L ( Λ , (( e L λ i Δ − 1 ) − 1 ) 1 ≤ i ≤ N , w ) = w ⋅ Λ − 1 ⋅ row-softmax ( P ) = w ⋅ Λ − 1 ⋅ row-softmax ( P )
递归视图
A ˉ = d i a g ( e λ 1 Δ , … , e λ N Δ ) A ˉ = diag ( e λ 1 Δ , … , e λ N Δ ) B ˉ = ( λ i − 1 ( e λ i Δ − 1 ) ) 1 ≤ i ≤ N B ˉ = ( λ i − 1 ( e λ i Δ − 1 ) ) 1 ≤ i ≤ N A ˉ = d i a g ( e λ 1 Δ , … , e λ N Δ ) A ˉ = diag ( e λ 1 Δ , … , e λ N Δ ) B ˉ = ( e λ i Δ − 1 λ i ( e λ i Δ L − 1 ) ) 1 ≤ i ≤ N B ˉ = ( λ i ( e λ i Δ L − 1 ) e λ i Δ − 1 ) 1 ≤ i ≤ N
解释
作为 LSTM 的遗忘门
如果ℜ ( λ ) < < 0 ℜ ( λ ) << 0 ℜ ( λ ) > > 0 ℜ ( λ ) >> 0
因此,我们在这里处理的是 ℂ,而不是 ℝ。
长版
GUPTA 提出了以下方案,以获得与 S4 具有相同表达能力的 DSS
令长度为 L L ( A , B , C ( A , B , C Δ > 0 Δ > 0 K ∈ R 1 × L K ∈ R 1 × L A ∈ C N × N A ∈ C N × N C C λ 1 , … , λ N λ 1 , … , λ N i ∀ i λ i ≠ 0 λ i = 0 e L λ i Δ ≠ 1 e L λ i Δ = 1 P ∈ C N × L P i , k = λ i k Δ P ∈ C N × L P i , k = λ i k Δ Λ Λ λ 1 , … , λ N λ 1 , … , λ N w ~ , w ∈ C 1 × N w , w ∈ C 1 × N
(a): K = K ˉ Δ , L ( Λ , ( 1 ) 1 ≤ i ≤ N , w ~ ) = w ~ ⋅ Λ − 1 ( e L a m b d a Δ − I ) ⋅ elementwise-exp ( P ) K = K ˉ Δ , L ( Λ , ( 1 ) 1 ≤ i ≤ N , w ) = w ⋅ Λ − 1 ( e L amb d a Δ − I ) ⋅ elementwise-exp ( P )
(b): K = K ˉ Δ , L ( Λ , ( ( e L a m b d a i Δ − 1 ) − 1 ) 1 ≤ i ≤ N , w ) = w ⋅ Λ − 1 ⋅ row-softmax ( P ) K = K ˉ Δ , L ( Λ , (( e L amb d a i Δ − 1 ) − 1 ) 1 ≤ i ≤ N , w ) = w ⋅ Λ − 1 ⋅ row-softmax ( P )
(a) 表明我们可以通过 Λ , w ~ ∈ C N Λ , w ∈ C N Λ Λ
2.1 卷积视角Λ Λ Λ = − elementwise-exp ( Λ r e ) + i ⋅ Λ i m Λ = − elementwise-exp ( Λ re ) + i ⋅ Λ im Δ = e x p ( Δ log ) ∈ R > 0 Δ = exp ( Δ l o g ) ∈ R > 0 K K Λ Λ Λ = Λ r e + i ⋅ Λ i m Λ = Λ re + i ⋅ Λ im Δ = e x p ( Δ log ) ∈ R > 0 Δ = exp ( Δ l o g ) ∈ R > 0 K K C C ( 0 , i π ) ( 0 , iπ )
2.2 循环视角A ˉ = d i a g ( e l a m b d a 1 Δ , … , e l a m b d a N Δ ) A ˉ = diag ( e l amb d a 1 Δ , … , e l amb d a N Δ ) B ˉ = ( λ i − 1 ( e l a m b d a i Δ − 1 ) ) 1 ≤ i ≤ N B ˉ = ( λ i − 1 ( e l amb d a i Δ − 1 ) ) 1 ≤ i ≤ N λ i λ i A ˉ A ˉ x k x k x i , k = e λ i Δ x i , k − 1 + λ i − 1 ( e λ i Δ − 1 ) u k x i , k = e λ i Δ x i , k − 1 + λ i − 1 ( e λ i Δ − 1 ) u k λ i ∣ Δ ≈ 0 λ i ∣Δ ≈ 0 x i , k ≈ x i , k − 1 x i , k ≈ x i , k − 1 R e ( λ i ) Δ ≪ 0 Re ( λ i ) Δ ≪ 0 i , k ≈ − λ i − 1 u k i , k ≈ − λ i − 1 u k
在 DSSsoftmax 中,使用上表中的循环公式,我们得到:A ˉ = d i a g ( e a m b d a 1 Δ , … , e a m b d a N Δ ) A ˉ = diag ( e amb d a 1 Δ , … , e amb d a N Δ ) b a r B = ( e a m b d a i Δ − 1 λ i ( e a m b d a i Δ L − 1 ) ) 1 ≤ i ≤ N ba r B = ( λ i ( e amb d a i Δ L − 1 ) e amb d a i Δ − 1 ) 1 ≤ i ≤ N x i , k = e λ i Δ x i , k − 1 + u k ( e λ i Δ − 1 ) λ i ( e λ i Δ L − 1 ) x i , k = e λ i Δ x i , k − 1 + λ i ( e λ i Δ L − 1 ) u k ( e λ i Δ − 1 ) e λ i Δ e λ i Δ R e ( λ ) Re ( λ ) x ~ k x k R e ( λ ) ≤ 0 Re ( λ ) ≤ 0 x ~ k = e λ Δ ⋅ x ~ k − 1 + u k , x k = x ~ k ⋅ ( e λ Δ − 1 ) λ ( e λ Δ L − 1 ) x k = e λ Δ ⋅ x k − 1 + u k , x k = x k ⋅ λ ( e λ Δ L − 1 ) ( e λ Δ − 1 )
特别地,如果 R e ( λ ) ≪ 0 Re ( λ ) ≪ 0 x ~ k ≈ u k x k ≈ u k x k ≈ u k / λ x k ≈ u k / λ
• 如果 R e ( λ ) > 0 Re ( λ ) > 0 x ~ k = x ~ k − 1 + e − k λ Δ ⋅ u k , x k = x ~ k ⋅ e l a m b d a Δ ( k − ( L − 1 ) ) λ ⋅ e − λ Δ − 1 e − λ Δ L − 1 x k = x k − 1 + e − kλ Δ ⋅ u k , x k = x k ⋅ λ e l amb d a Δ ( k − ( L − 1 )) ⋅ e − λ Δ L − 1 e − λ Δ − 1
类似地,如果 R e ( λ ) ≫ 0 Re ( λ ) ≫ 0 x ~ 0 ≈ u 0 x 0 ≈ u 0 x ~ k ≈ x ~ k − 1 ≈ u 0 x k ≈ x k − 1 ≈ u 0 x k < L − 1 ≈ 0 x k < L − 1 ≈ 0 x L − 1 ≈ u 0 / λ x L − 1 ≈ u 0 / λ L L t → ∞ t → ∞ K ( t ) = C exp ( A ⊺ ) . B ) K ( t ) = C exp ( A ⊺ ) . B ) R e ( λ ) ≫ 0 Re ( λ ) ≫ 0
3. 初始化 w w N ( 0 , 1 ) N ( 0 , 1 ) Δ log Δ l o g exp ( U ( l o g ( 0.001 ) , l o g ( 0.1 ) ) ) exp ( U ( l o g ( 0.001 ) , l o g ( 0.1 ))) Δ Δ Δ Δ
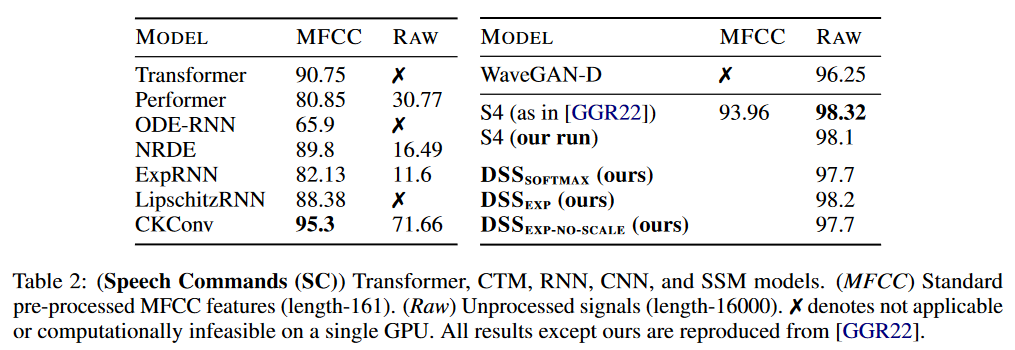
关于结果,DSS 已在 LRA 和 WARDEN (2018) 的 Speech Commands
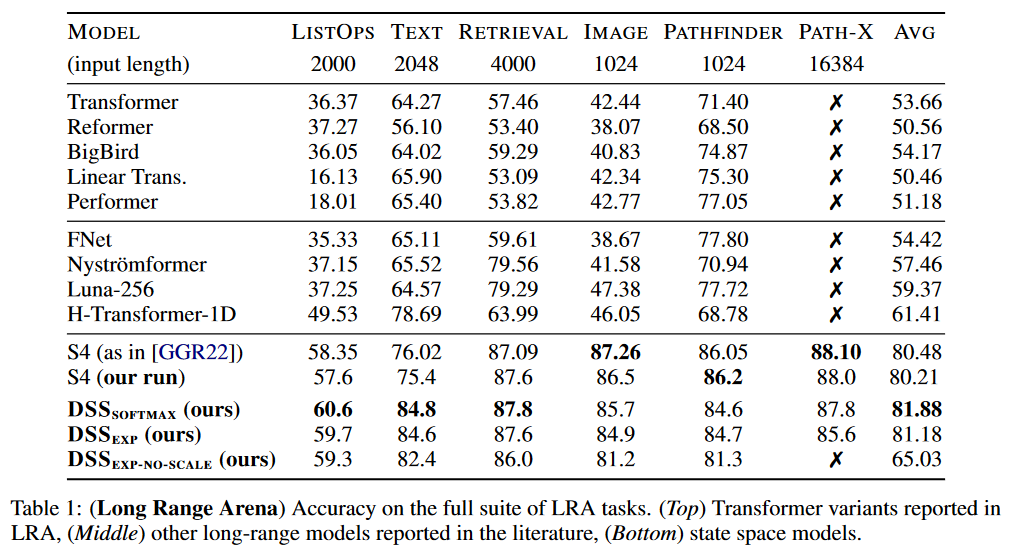
图 6:LRA 上的 DSS 结果
对于此基准,DSS(softmax 或 exp 版本)实现了比原始 S4 更好的平均结果。DSSsoftmax 似乎比 DSSexp 表现稍好。这篇论文的另一个有趣之处在于,它是第一篇重现 S4 结果的论文,从而证实 SSM 通过了此基准测试。
图 7:Speech Commands 上的 DSS 结果
在 Speech Commands 上,S4 保持了其对 DSS 的优势。
深入探讨 GitHub 上获取。NeurIPS 2022 上的 spotlight talk 的主题。
S4D:对角线 S4
2022 年 6 月 23 日,GU、GUPTA 等人在他们的论文 On the Parameterization and Initialization of Diagonal State Space Models A A
论文表 1 对这三种方法进行了比较
图 8:S4、DSS 和 S4D 的比较
S4D 可以使用 S4 的双线性离散化或 DSS 的 ZOH 离散化。
在 S4D 中,方程 y = u ∗ K ‾ y = u ∗ K K ‾ ℓ = ∑ n = 0 N − 1 C n A ‾ n ℓ B ‾ n ⟹ K ‾ = ( B ‾ ⊤ ∘ C ) ⋅ V L ( A ‾ ) K ℓ = ∑ n = 0 N − 1 C n A n ℓ B n ⟹ K = ( B ⊤ ∘ C ) ⋅ V L ( A ) ∘ ∘ Hadamard 矩阵积 ,⋅ ⋅ V L V L 范德蒙矩阵 ,即:V = [ 1 α 1 α 1 2 … α 1 n − 1 1 α 2 α 2 2 … α 2 n − 1 1 α 3 α 3 2 … α 3 n − 1 ⋮ ⋮ ⋮ ⋮ 1 α m α m 2 … α m n − 1 ] V = 1 1 1 ⋮ 1 α 1 α 2 α 3 ⋮ α m α 1 2 α 2 2 α 3 2 ⋮ α m 2 … … … ⋮ … α 1 n − 1 α 2 n − 1 α 3 n − 1 α m n − 1
换句话说,对于任意i i j j i i j j V i , j = α i j − 1 V i , j = α i j − 1
最后,在 S4D 中,
K ‾ = [ B ‾ 0 C 0 … B ‾ N − 1 C N − 1 ] [ 1 A ‾ 0 A ‾ 0 2 … A ‾ 0 L − 1 1 A ‾ 1 A ‾ 1 2 … A ‾ 1 L − 1 ⋮ ⋮ ⋮ ⋱ ⋮ 1 A ‾ N − 1 A ‾ N − 1 2 … A ‾ N − 1 L − 1 ] where V L ( A ‾ ) n , ℓ = A ‾ n ℓ K = [ B 0 C 0 … B N − 1 C N − 1 ] 1 1 ⋮ 1 A 0 A 1 ⋮ A N − 1 A 0 2 A 1 2 ⋮ A N − 1 2 … … ⋱ … A 0 L − 1 A 1 L − 1 ⋮ A N − 1 L − 1 其中 V L ( A ) n , ℓ = A n ℓ
所有计算都在O ( N + L ) O ( N + L )
各种矩阵的参数化如下:
A = − exp ( ℜ ( A ) ) + i ⋅ ℑ ( A ) A = − exp ( ℜ ( A )) + i ⋅ ℑ ( A ) B = 1 B = 1 C C
请注意,S4 考虑实数,而 S4D 通过将状态大小参数化为 N / 2 N /2 N N
关于初始化,作者介绍了两种方法:
S4D-Inv 是 S4-LegS 的近似值:A n = − 1 2 + i N π ( N 2 n + 1 − 1 ) A n = − 2 1 + i π N ( 2 n + 1 N − 1 ) S4D-Lin 是 S4-FouT 的近似值:A n = − 1 2 1 + i π n A n = − 2 1 1 + iπn
我们邀请读者参阅论文的第 4 部分,了解这些方程的更多细节。A n A n A n A n K n ( t ) = e t A B K n ( t ) = e t A B
最后,作者提出了一些结果:
用 Softmax 代替 Vandermonde 计算模型,效果没有太大差异。
训练 B 总是能得到更好的结果。
两种可能的离散化之间没有显著差异。
限制 A 的实部会带来更好的结果(尽管不显著)。
所有测试的初始化修改都降低了结果。即,对虚部应用系数或使用随机虚部/使用随机实部/使用虚部和随机实部。
由于这种方法比其他方法更容易实现(Vandermade 只需要两行代码),S4D 已取代 S4 成为常用方法(实际上,例如在 Mamba 论文的表 6 中,作者使用术语 S4 来指代 S4D)。
深入探讨 GitHub 上获取。Simplifying and Understanding State Space Models with Diagonal Linear RNNs GitHub 上获取。
GSS: 门控状态空间(Gated State Space)
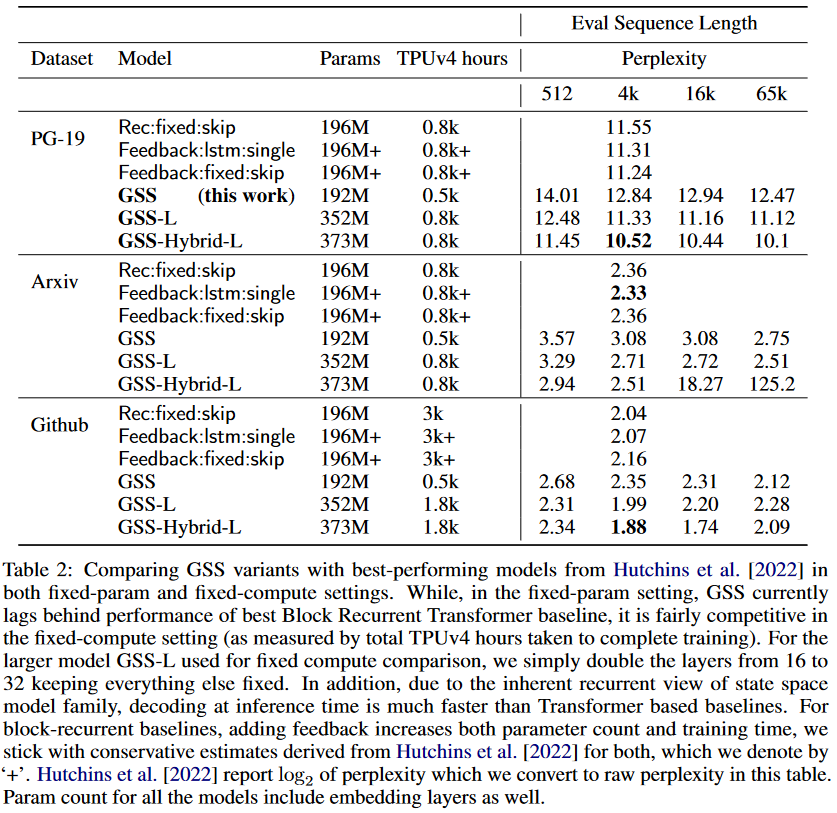
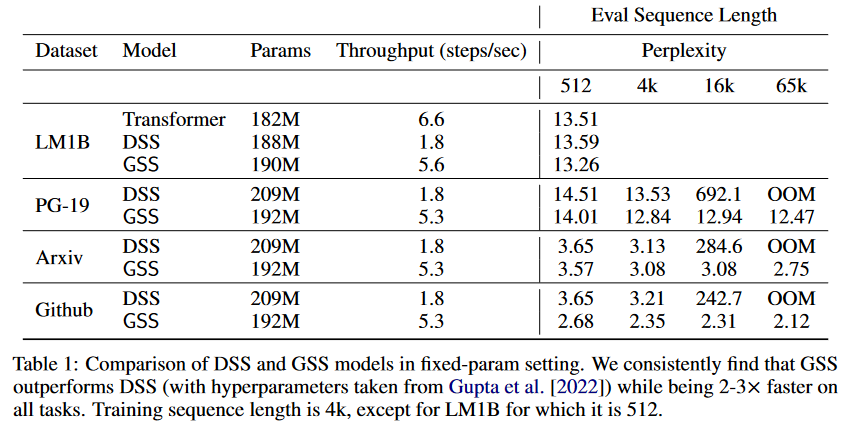
在 S4D 发布的五天后,即 2022 年 6 月 27 日,MEHTA、GUPTA 等人在他们的论文《Long Range Language Modeling via Gated State Spaces
图 9:DSS 与 GSS 的比较。模型在 4K 长度的序列上进行训练,然后在长达 65K 令牌的序列上进行评估。
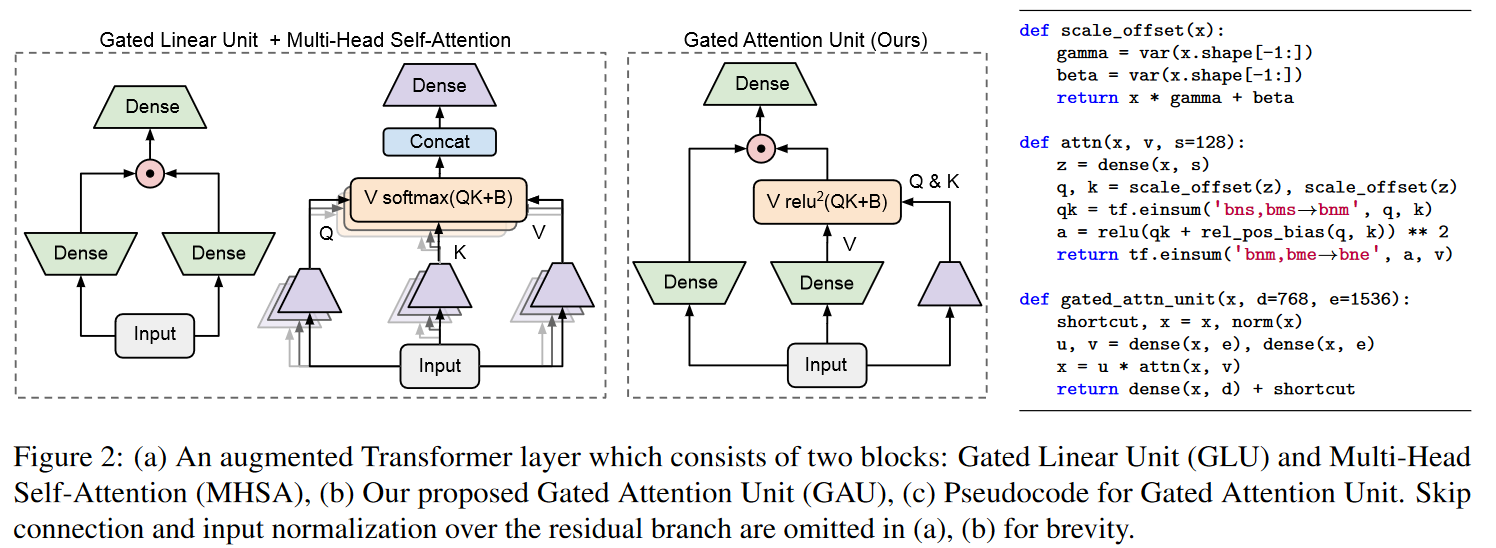
基于 SSM(S4/DSS)在 TPU 上训练速度慢于预期的观察结果,作者修改了架构,以减少特定操作的维度,这些操作被证明是瓶颈。这些修改的灵感来自于关于门控单元效率的经验观察(DAUPHIN 等人(2016)的《Language Modeling with Gated Convolutional Networks GLU Variants Improve Transformer Transformer Quality in Linear Time
图 10:门控注意力单元。
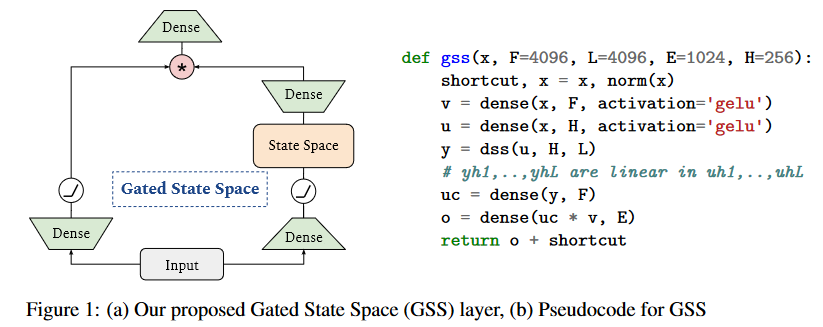
因此,GSS 的作者将门控单元的使用扩展到 SSM,并观察到在执行 FFT 操作时维度有所降低。
图 11:GAU 在 SSM 中的应用。
值得注意的是,与 HUA 等人不同,作者没有观察到使用 RELU² 或 Swish 激活函数而不是 GELU 有多少优势,因此保留了 GELU。∆ ∆
至于 GSS-Transformer 混合模型,它只是稀疏地将传统 Transformer 块与 GSS 层交织在一起。混合模型实现了比纯 SSM 模型更低的困惑度。
图 12:GSS-Transformer 混合模型的性能。
深入探讨 GitHub 上获取。
Mega
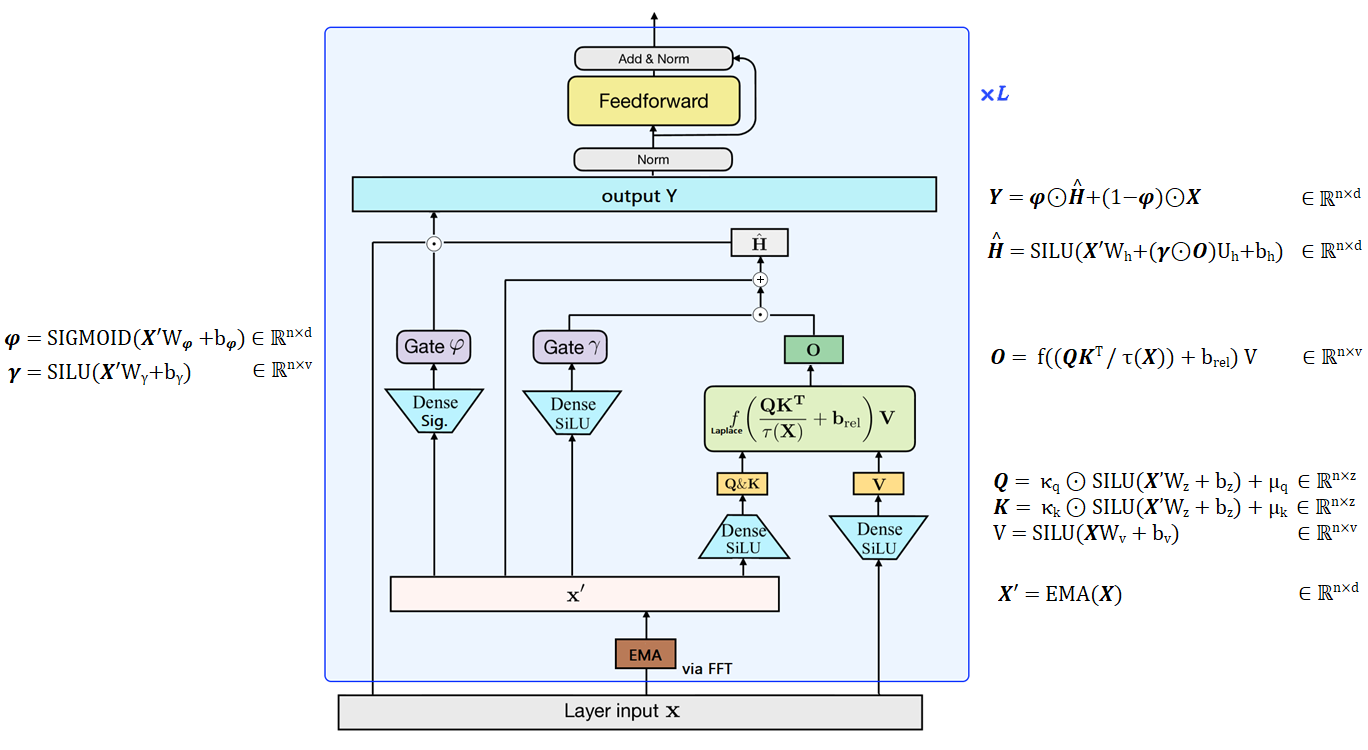
2022 年 9 月 21 日,MA、ZHOU 等人发表了《Mega: Moving Average Equipped Gated Attention
图 13:Mega 概述,根据我对论文的理解设计的图。
作者还提出了一个变体,Mega-chunk,它有效地将整个序列分成几个固定长度的块。在这里,他们采用了 FLASH 模型中已经存在并解释的原理(参见该模型论文的图 4)。这提供了线性的时间复杂度和空间复杂度,同时质量损失最小。
图 14:Mega 分块
这提供了线性复杂度,只需将注意力局部应用于每个固定长度的块。c c Q = Q 1 , . . . Q k Q = Q 1 , ... Q k k = − n c k = − c n n n O ( k c 2 ) = O ( n c ) O ( k c 2 ) = O ( n c )
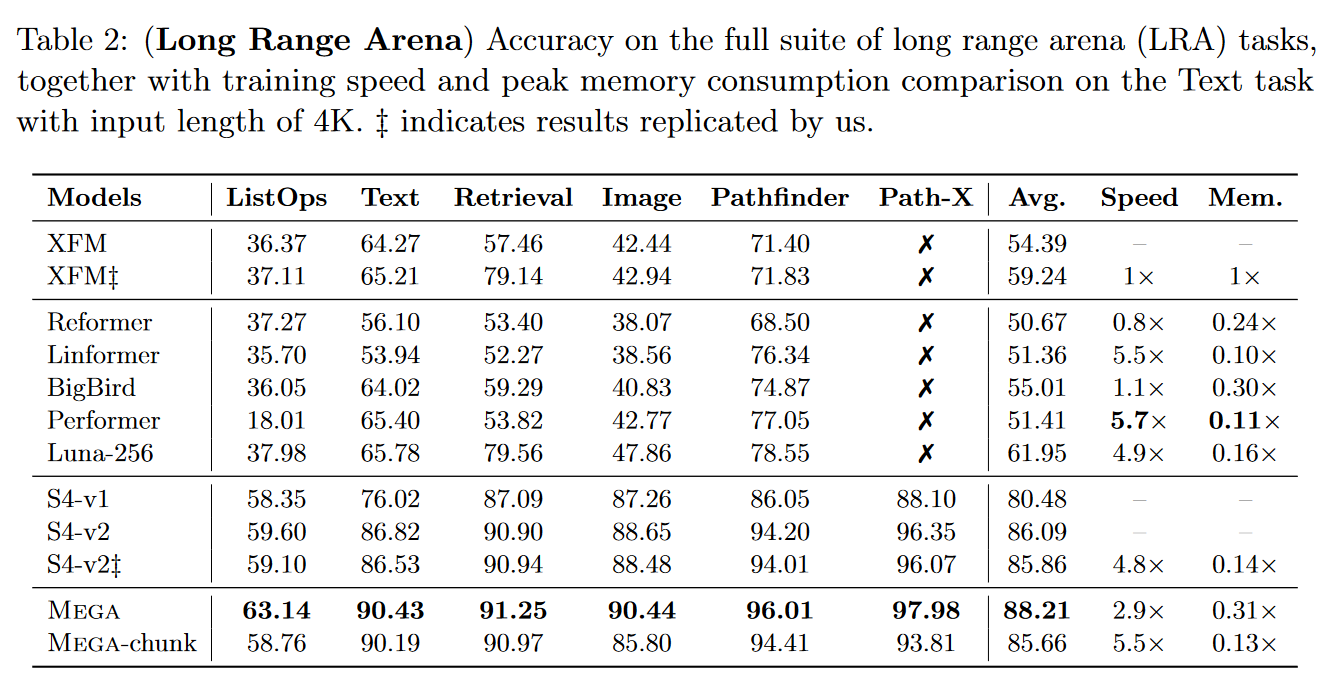
Mega 极具竞争力,因为它成为 LRA 上最好的模型。
图 15:Mega 在 LRA 基准测试中的结果
那么,Transformer 在一篇关于 SSM 的博客文章中做什么呢?让我们看看阻尼 EMA 以了解 Mega 和 S4D 之间的联系。
• “经典” EMA 提醒 𝐲 t = 𝜶 ⊙ 𝐱 t + ( 1 − 𝜶 ) ⊙ 𝐲 t − 1 y t = 𝜶 ⊙ x t + ( 1 − 𝜶 ) ⊙ y t − 1 𝜶 𝜶 [ 0 , 1 ] d [ 0 , 1 ] d
• Mega 中使用的 EMA 𝐲 t = 𝜶 ⊙ 𝐱 t + ( 1 − 𝜶 ⊙ 𝜹 ) ⊙ 𝐲 t − 1 y t = 𝜶 ⊙ x t + ( 1 − 𝜶 ⊙ 𝜹 ) ⊙ y t − 1 𝜹 𝜹 [ 0 , 1 ] d [ 0 , 1 ] d x x R d × h R d × h 𝜷 𝜷 h h 𝐲 t , j = 𝜼 j ⊺ 𝐡 t ( j ) y t , j = 𝜼 j ⊺ h t ( j ) 𝐡 t ( j ) = 𝜶 j ⊙ 𝐮 t ( j ) + ( 1 − 𝜶 j ⊙ 𝜹 j ) ⊙ 𝐡 t − 1 ( j ) h t ( j ) = 𝜶 j ⊙ u t ( j ) + ( 1 − 𝜶 j ⊙ 𝜹 j ) ⊙ h t − 1 ( j ) 𝜼 ∈ R d × h 𝜼 ∈ R d × h h h 𝐲 t , j ∈ R y t , j ∈ R
证明多维“阻尼”EMA 可以通过卷积计算,因此可以通过 FTT 计算(通过将 d = 1 d = 1 𝜶 𝜶 𝜹 𝜹
我们有 𝐲 t = 𝜼 ⊺ 𝐡 t y t = 𝜼 ⊺ h t 𝐡 t = 𝜶 j ⊙ 𝐮 t + ( 1 − 𝜶 ⊙ 𝜹 ) ⊙ 𝐡 t − 1 h t = 𝜶 j ⊙ u t + ( 1 − 𝜶 ⊙ 𝜹 ) ⊙ h t − 1 ϕ = 1 − 𝜶 ⊙ 𝜹 ϕ = 1 − 𝜶 ⊙ 𝜹 𝐡 t = 𝜶 ⊙ 𝐮 t + ( 1 − 𝜶 ⊙ 𝜹 ) ⊙ 𝐡 t − 1 = 𝜶 ⊙ 𝜷 𝐱 t + ϕ ⊙ 𝐡 t − 1 h t = 𝜶 ⊙ u t + ( 1 − 𝜶 ⊙ 𝜹 ) ⊙ h t − 1 = 𝜶 ⊙ 𝜷 x t + ϕ ⊙ h t − 1 𝐲 t = 𝜼 ⊺ 𝐡 t = 𝜼 ⊺ ( 𝜶 ⊙ 𝜷 𝐱 t + ϕ ⊙ 𝐡 t − 1 ) y t = 𝜼 ⊺ h t = 𝜼 ⊺ ( 𝜶 ⊙ 𝜷 x t + ϕ ⊙ h t − 1 ) 𝐡 1 = 𝜶 ⊙ 𝜷 𝐱 1 + ϕ ⊙ 𝐡 0 h 1 = 𝜶 ⊙ 𝜷 x 1 + ϕ ⊙ h 0 𝐡 2 = 𝜶 ⊙ 𝜷 𝐱 2 + ϕ ⊙ 𝐡 1 h 2 = 𝜶 ⊙ 𝜷 x 2 + ϕ ⊙ h 1 = 𝜶 ⊙ 𝜷 𝐱 2 + ϕ ⊙ ( ϕ ⊙ 𝐡 0 + 𝜶 ⊙ 𝜷 𝐱 1 ) = 𝜶 ⊙ 𝜷 𝐱 2 + ϕ 2 ⊙ 𝐡 0 + ϕ ⊙ 𝜶 ⊙ 𝜷 𝐱 1 = 𝜶 ⊙ 𝜷 x 2 + ϕ ⊙ ( ϕ ⊙ h 0 + 𝜶 ⊙ 𝜷 x 1 ) = 𝜶 ⊙ 𝜷 x 2 + ϕ 2 ⊙ h 0 + ϕ ⊙ 𝜶 ⊙ 𝜷 x 1
同理𝐲 1 = 𝜼 ⊺ 𝜶 ⊙ 𝜷 𝐱 1 + ϕ ⊙ 𝐡 0 ) = 𝜼 ⊺ 𝜶 ⊙ 𝜷 𝐱 1 + 𝜼 ⊺ ϕ ⊙ 𝐡 0 y 1 = 𝜼 ⊺ 𝜶 ⊙ 𝜷 x 1 + ϕ ⊙ h 0 ) = 𝜼 ⊺ 𝜶 ⊙ 𝜷 x 1 + 𝜼 ⊺ ϕ ⊙ h 0 𝐲 2 = 𝜼 ⊺ 𝜶 ⊙ 𝜷 𝐱 2 + 𝜼 ⊺ ϕ ⊙ 𝐡 1 y 2 = 𝜼 ⊺ 𝜶 ⊙ 𝜷 x 2 + 𝜼 ⊺ ϕ ⊙ h 1 = 𝜼 ⊺ 𝜶 ⊙ 𝜷 𝐱 2 + 𝜼 ⊺ ϕ ⊙ ( 𝜶 ⊙ 𝜷 𝐱 1 + ϕ ⊙ 𝐡 0 ) = 𝜼 ⊺ 𝜶 ⊙ 𝜷 𝐱 2 + 𝜼 ⊺ ϕ 2 ⊙ 𝐡 0 = 𝜼 ⊺ 𝜶 ⊙ 𝜷 x 2 + 𝜼 ⊺ ϕ ⊙ ( 𝜶 ⊙ 𝜷 x 1 + ϕ ⊙ h 0 ) = 𝜼 ⊺ 𝜶 ⊙ 𝜷 x 2 + 𝜼 ⊺ ϕ 2 ⊙ h 0 t t 𝐲 t = 𝜼 ⊺ 𝜶 ⊙ 𝜷 𝐱 t + . . . + 𝜼 ⊺ ϕ t − 1 ⊙ 𝜶 ⊙ 𝜷 𝐱 t − 1 + 𝜼 ⊺ ϕ t ⊙ 𝐡 0 y t = 𝜼 ⊺ 𝜶 ⊙ 𝜷 x t + ... + 𝜼 ⊺ ϕ t − 1 ⊙ 𝜶 ⊙ 𝜷 x t − 1 + 𝜼 ⊺ ϕ t ⊙ h 0
因此 𝐲 = K ∗ 𝐱 + 𝜼 ⊺ ϕ t ⊙ 𝐡 0 y = K ∗ x + 𝜼 ⊺ ϕ t ⊙ h 0 K = ( 𝜼 ⊺ ( 𝜶 ⊙ 𝜷 ) , 𝜼 ⊺ ( ϕ ⊙ 𝜶 ⊙ 𝜷 ) , . . . , 𝜼 ⊺ ( ϕ t ⊙ 𝜶 ⊙ 𝜷 ) ∈ R n K = ( 𝜼 ⊺ ( 𝜶 ⊙ 𝜷 ) , 𝜼 ⊺ ( ϕ ⊙ 𝜶 ⊙ 𝜷 ) , ... , 𝜼 ⊺ ( ϕ t ⊙ 𝜶 ⊙ 𝜷 ) ∈ R n K K
深入探讨 GitHub 上获取。Transformers 上获取。Open Review 上对 Mega 提交的评论中交换的消息。总而言之,通过将 SSM 离散化步骤与阻尼 EMA 相关联,可以将 Mega 视为混合 SSM/Attention,从而简化 S4 为实值而非复数。
2022 年 9 月 26 日,HASANI, LECHNER 等人在线发布了 Liquid Structural State-Space Models 液体时间常数 )的近似能力。液体时间常数网络
d x ( t ) d t = − [ A + B ⊙ f ( x ( t ) , u ( t ) , t , θ ) ] ⏟ Liquid time-constant ⊙ x ( t ) + B ⊙ f ( x ( t ) , u ( t ) , t , θ ) . d t d x ( t ) = − Liquid time-constant [ A + B ⊙ f ( x ( t ) , u ( t ) , t , θ ) ] ⊙ x ( t ) + B ⊙ f ( x ( t ) , u ( t ) , t , θ ) .
其中
x ( N × 1 ) ( t ) x ( N × 1 ) ( t ) N N u ( m × 1 ) ( t ) u ( m × 1 ) ( t ) m m A ( N × 1 ) A ( N × 1 ) B ( N × 1 ) B ( N × 1 ) ⊙ ⊙ f ( . ) f ( . ) θ θ
在实践中,使用液体网络的 SSM 通过以下微分方程系统进行公式化:
x ′ = ( A + B u ) x + B u y = C x x ′ y = ( A + B u ) x + B u = C x
这个动态系统可以通过与 S4 相同的参数化有效求解,从而产生一个额外的卷积核,该卷积核考虑了移位信号的相似性。由此产生的模型是 Liquid-S4。我们用一点数学来解释这一点。
Liquid-S4 的循环视图是通过使用梯形法则(双线性形式)离散化系统获得的。结果是
x k = ( A ‾ + B ‾ u k ) x k − 1 + B ‾ u k , y k = C ‾ x k x k = ( A + B u k ) x k − 1 + B u k , y k = C x k
与 S4 一样,通过在时间上展开递归视图(假设 x − 1 = 0 x − 1 = 0
x 0 = B ‾ u 0 y 0 = C ‾ B ‾ u 0 x 1 = A ‾ B ‾ u 0 + B ‾ u 1 + B ‾ 2 u 0 u 1 y 1 = C ‾ A ‾ B ‾ u 0 + C ‾ B ‾ u 1 + C ‾ B ‾ 2 u 0 u 1 x 2 = A ‾ 2 B ‾ u 0 + A ‾ B ‾ u 1 + B ‾ u 2 + A ‾ B ‾ 2 u 0 u 1 + A ‾ B ‾ 2 u 0 u 2 + B ‾ 2 u 1 u 2 + B ‾ 3 u 0 u 1 u 2 y 2 = C ‾ A ‾ 2 B ‾ u 0 + C ‾ A ‾ B ‾ u 1 + C ‾ B ‾ u 2 + C ‾ A ‾ B ‾ 2 u 0 u 1 + C ‾ A ‾ B ‾ 2 u 0 u 2 + C ‾ B ‾ 2 u 1 u 2 + C ‾ B ‾ 3 u 0 u 1 u 2 , … y k = C ‾ A ‾ k B ‾ u 0 + C ‾ A ‾ k − 1 B ‾ u 1 + … C ‾ A ‾ B ‾ u k − 1 + C ‾ B ‾ u k + ∑ p = 2 P ∀ ( k + 1 p ) of u i u i + 1 … u p C ‾ A ‾ ( k + 1 − p − i ) B ‾ p u i u i + 1 … u p for i ∈ Z and i ≥ 0 → y = K ‾ ∗ u + K ‾ liquid ∗ u correlations x 0 y 0 x 1 y 1 x 2 y 2 y k = B u 0 = C B u 0 = A B u 0 + B u 1 + B 2 u 0 u 1 = C A B u 0 + C B u 1 + C B 2 u 0 u 1 = A 2 B u 0 + A B u 1 + B u 2 + A B 2 u 0 u 1 + A B 2 u 0 u 2 + B 2 u 1 u 2 + B 3 u 0 u 1 u 2 = C A 2 B u 0 + C A B u 1 + C B u 2 + C A B 2 u 0 u 1 + C A B 2 u 0 u 2 + C B 2 u 1 u 2 + C B 3 u 0 u 1 u 2 , … = C A k B u 0 + C A k − 1 B u 1 + … C A B u k − 1 + C B u k + p = 2 ∑ P ∀ ( p k + 1 ) of u i u i + 1 … u p C A ( k + 1 − p − i ) B p u i u i + 1 … u p for i ∈ Z and i ≥ 0 → y = K ∗ u + K liquid ∗ u correlations
你可以在公式中看到两种颜色。它们对应于两种类型的权重配置
黑色部分,是独立时间输入的权重,即 S4 的卷积核。
紫色部分,是与输入信号所有阶自相关相关的权重。这是一个额外的输入相关核,作者称之为液体核。
最后,卷积核表达如下:
K ‾ liquid ∈ R L ~ : = K L ( C ‾ , A ‾ , B ‾ ) : = ( C ‾ A ‾ ( L ~ − i − p ) B ‾ p ) i ∈ [ L ~ ] , p ∈ [ P ] = ( C ‾ A ‾ L ~ − 2 B ‾ 2 , … , C ‾ B ‾ p ) K liquid ∈ R L ~ := K L ( C , A , B ) := ( C A ( L ~ − i − p ) B p ) i ∈ [ L ~ ] , p ∈ [ P ] = ( C A L ~ − 2 B 2 , … , C B p )
作者随后指出,这可以通过类似于 S4 中应用的过程(HiPPO、Woodbury、逆傅里叶变换等)高效计算。有关更多细节,请参阅论文中的算法 1。
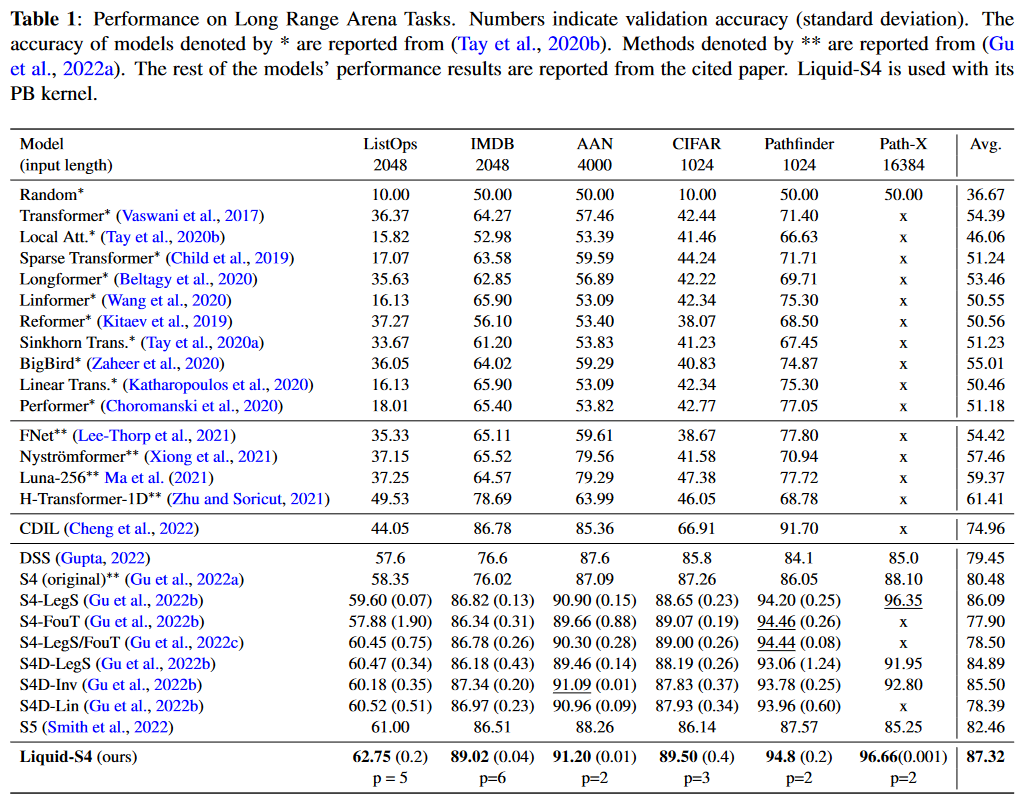
在 LRA 上测试,这种方法似乎是最好的。只有 Mega(早几天发布,因此未出现在论文中)表现更好
图 16:Liquid-S4 在 LRA 基准测试上的结果
HASANI、LECHNER 等人还将他们的模型应用于 PIMENTEL 等人的 Speech Commands、sCIFAR 和 BIDMC Vital Signs 数据集,并建立了新的最先进水平。
深入探讨 GitHub 上获取。Open Review 上的交流。GitHub 上获取。
S5:序列建模的简化状态空间层
按时间顺序,SMITH、WARRINGTON 和 LINDERMAN 引入 S5 模型的论文 Simplified State Space Layers for Sequence Modeling
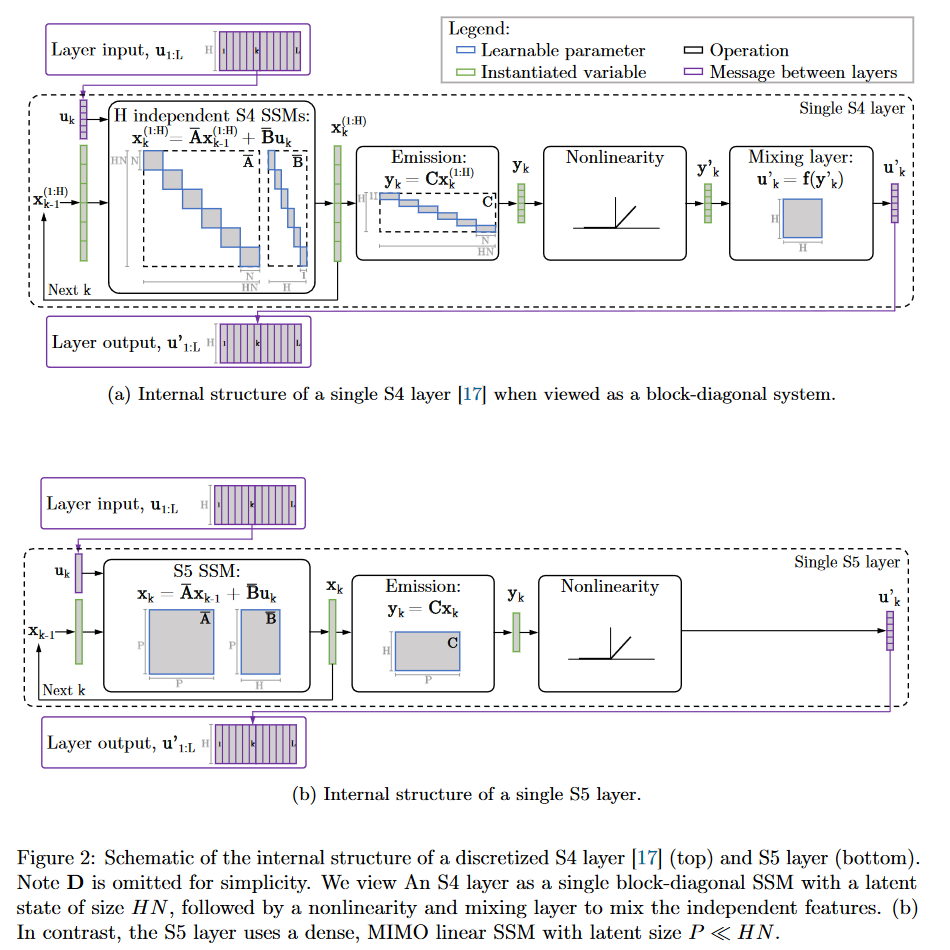
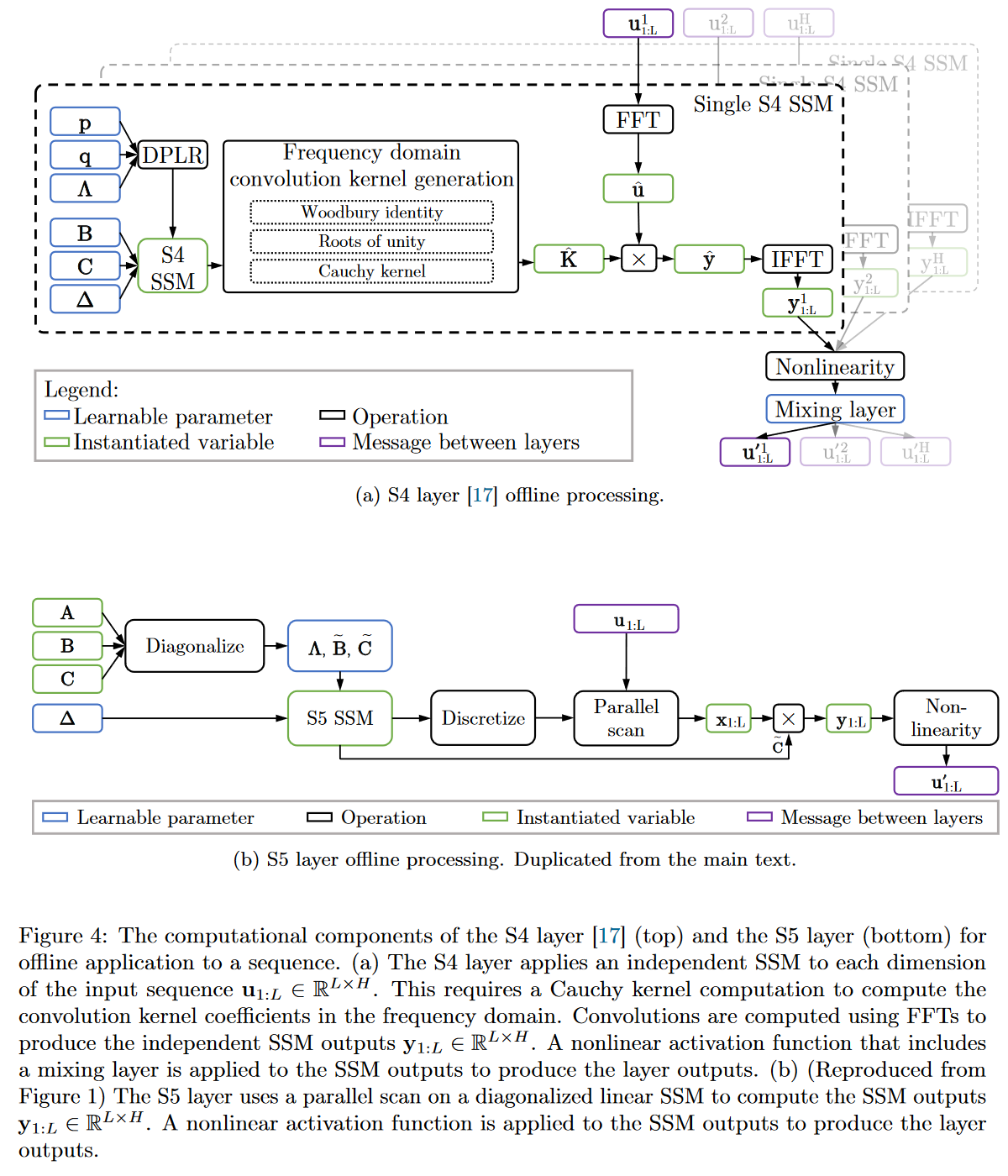
在 S5 中,作者提出用多输入/多输出 (MIMO) SSM 代替 S4 的单输入/单输出 (SISO) SSM 库的公式,该 MIMO SSM 具有减小的潜在维度。
图 17:S4 与 S5 内部行为比较
MIMO 系统减小的潜在维度允许使用并行扫描 算法,这简化了将 S5 层作为序列到序列转换所需的计算。因此,由此产生的模型失去了 SSM 的卷积视图,而只关注循环视图(通过 ZOH 离散化获得)。作者的方法是在时域而不是频域中操作。他们使用 HiPPO 矩阵的对角近似,从而为其 MIMO 系统实现高效的初始化和参数化。
图 19:S4 与 S5 行为的完整比较
由于未来其他 SSM(特别是 Mamba)也会使用并行扫描 ,让我们仔细看看它在 S5 中的工作原理,以便从本文开始就熟悉此算法。最简单的方法是使用论文附录 H 中给出的示例,其中作者将其应用于长度为 L = 4 L = 4
要计算并行扫描 ,需要两件事
扫描将操作的初始元素。L L c 1 : L c 1 : L c k c k c k = ( c k , a , c k , b ) : = ( A ‾ , B ‾ u k ) c k = ( c k , a , c k , b ) := ( A , B u k ) L = 4 L = 4 ( A ‾ , B ‾ u 1 ) , ( A ‾ , B ‾ u 2 ) , ( A ‾ , B ‾ u 3 ) ( A , B u 1 ) , ( A , B u 2 ) , ( A , B u 3 ) ( A ‾ , B ‾ u 4 ) ( A , B u 4 )
用于组合元素的二元结合运算符。数学上,二元结合运算符是 I ∙ J ∙ K = ( I ∙ J ) ∙ K = I ∙ ( J ∙ K ) I ∙ J ∙ K = ( I ∙ J ) ∙ K = I ∙ ( J ∙ K )
如果我们按顺序进行扫描 ,令 s 0 : = ( I , 0 ) s 0 := ( I , 0 ) s i s i s 1 = s 0 ∙ c 1 = ( I , 0 ) ∙ ( A ‾ , B ‾ u 1 ) = ( A ‾ I , A ‾ 0 + B ‾ u 1 ) = ( A ‾ , B ‾ u 1 ) s 1 = s 0 ∙ c 1 = ( I , 0 ) ∙ ( A , B u 1 ) = ( A I , A 0 + B u 1 ) = ( A , B u 1 ) s 2 = s 1 ∙ c 2 = ( A ‾ , B ‾ u 1 ) ∙ ( A ‾ , B ‾ u 2 ) = ( A ‾ 2 , A ‾ B ‾ u 1 + B ‾ u 2 ) s 2 = s 1 ∙ c 2 = ( A , B u 1 ) ∙ ( A , B u 2 ) = ( A 2 , A B u 1 + B u 2 ) s 3 = s 2 ∙ c 3 = ( A ‾ 2 , A ‾ B ‾ u 1 + B ‾ u 2 ) ∙ ( A ‾ , B ‾ u 3 ) = ( A ‾ 3 , A ‾ 2 B ‾ u 1 + A ‾ B ‾ u 2 + B ‾ u 3 ) s 3 = s 2 ∙ c 3 = ( A 2 , A B u 1 + B u 2 ) ∙ ( A , B u 3 ) = ( A 3 , A 2 B u 1 + A B u 2 + B u 3 ) s 4 = s 3 ∙ c 4 = ( A ‾ 3 , A ‾ 2 B ‾ u 1 + A ‾ B ‾ u 2 + B ‾ u 3 ) ∙ ( A ‾ , B ‾ u 4 ) = ( A ‾ 4 , A ‾ 3 B ‾ u 1 + A ‾ 2 B ‾ u 2 + A ‾ B ‾ u 3 + B ‾ u 4 ) . s 4 = s 3 ∙ c 4 = ( A 3 , A 2 B u 1 + A B u 2 + B u 3 ) ∙ ( A , B u 4 ) = ( A 4 , A 3 B u 1 + A 2 B u 2 + A B u 3 + B u 4 ) .
为了获得 x i x i s i s i
按顺序处理并非最有效的方式,因为可以通过并行扫描(parallel scan) 来并行化计算递推关系。以下是它在我们长度为 L L
图 19:S5 中并行扫描的工作原理
同样,要获得 x i x i s i s i s 2 s 2 i 4 i 4 s 1 s 1 s 3 s 3 s 4 s 4 并行扫描 的复杂度是 O ( l o g ( L ) ) O ( l o g ( L ))
图 20:并行扫描的工作原理(一般情况)。基于 Scott Linderman 的动画。
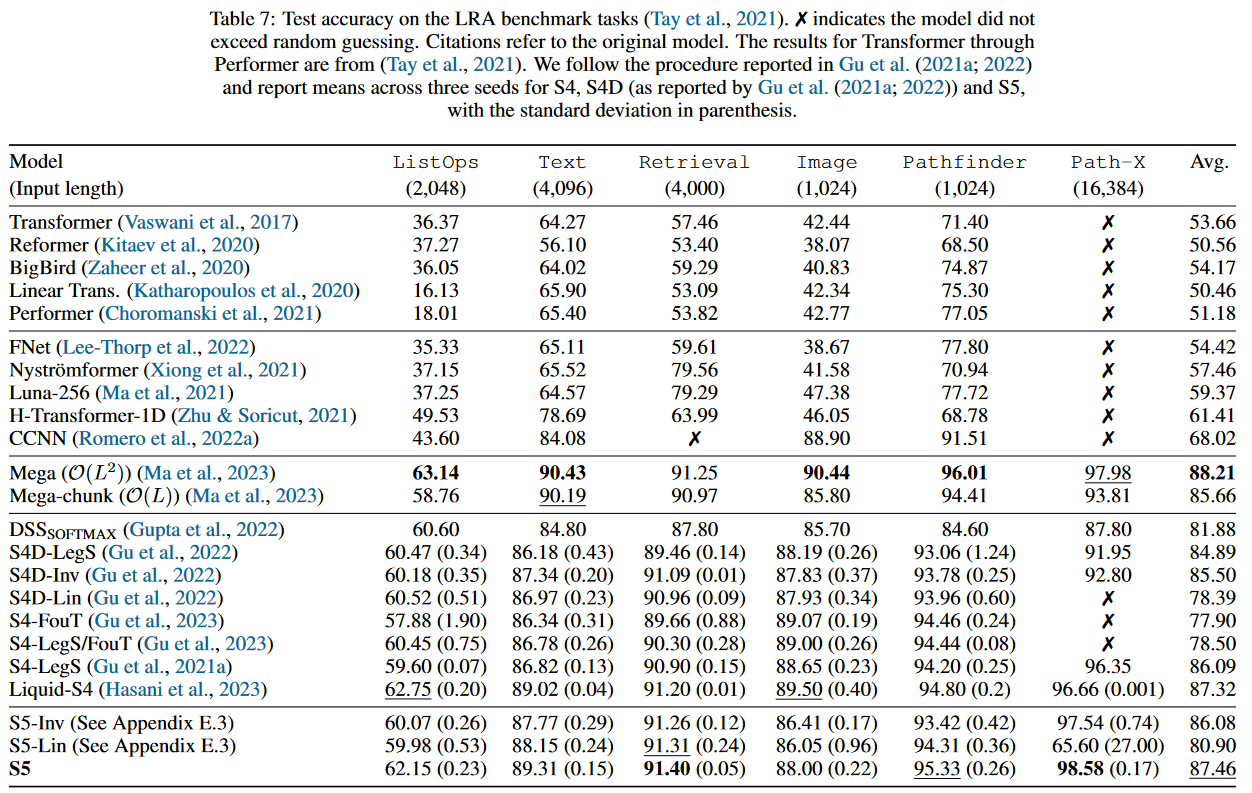
在性能方面,S5 在 LRA 上排名第二。
图 21:S5 在 LRA 基准测试上的结果
除了 LRA,S5 的作者还在 语音命令(Speech Commands) 、摆锤回归数据集(pendulum regression dataset) 以及 sMNIST 、psMNIST 和 sCIFAR 上比较了他们的模型。完整的结果可在论文的附录中找到,其中还包含一项消融研究(ablation study)。
深入探讨 GitHub 上获取。Open Review 上的讨论。
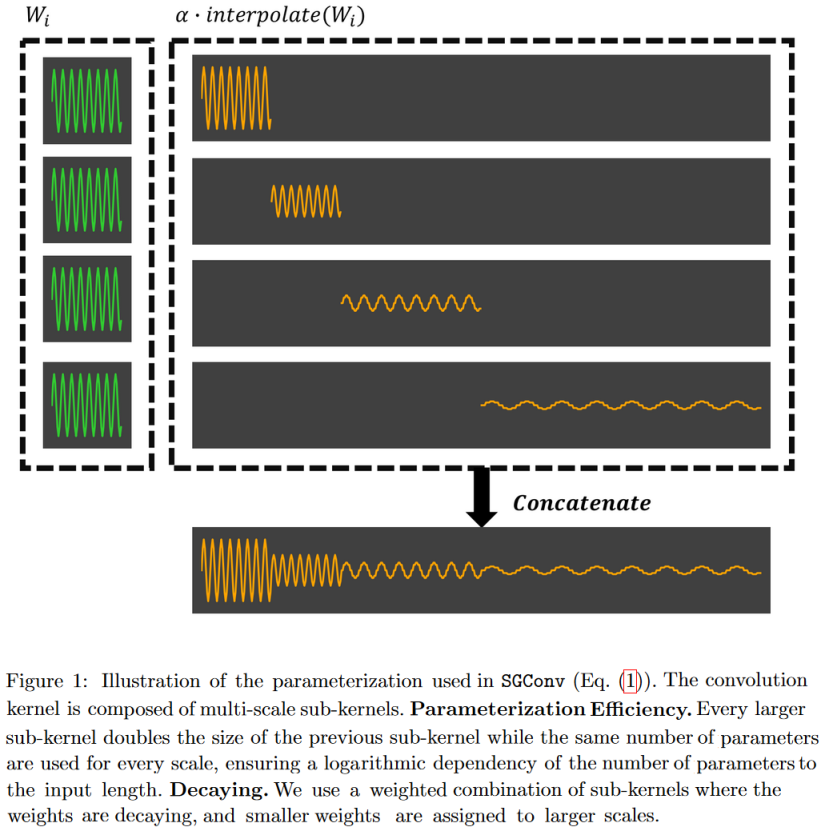
SGConv
2022 年 10 月 17 日,LI、CAI 等人在其论文 What Makes Convolutional Models Great on Long Sequence Modeling?
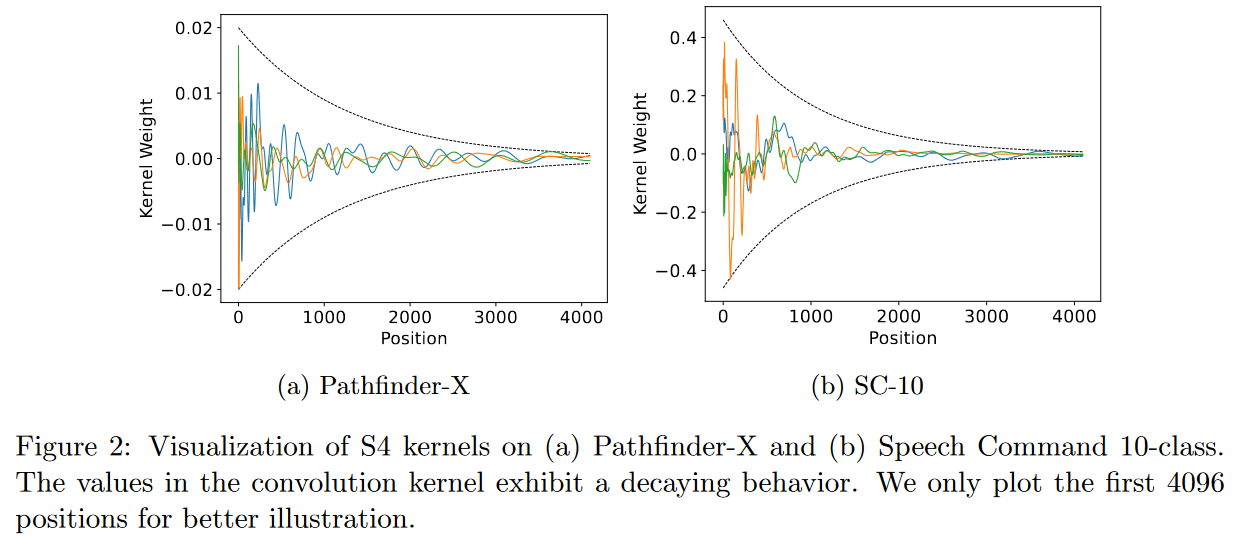
卷积核的参数化必须高效,即参数数量必须与序列长度呈次线性增长。
核必须具有递减结构,其中与最近邻居的卷积权重大于与最远邻居的卷积权重。
图 22:遵守作者提出的两个关键原则意味着卷积核应与图中所示的相似。
基于这两个原则,他们提出了一种高效的卷积模型,名为结构化全局卷积(Structured Global Convolution,SGConv)。
图 23:SGConv 将卷积核构建为连续的、长度更长、范数更低的弦函数的连接。这种形式的优点是它可以在频域实现非常快的卷积。
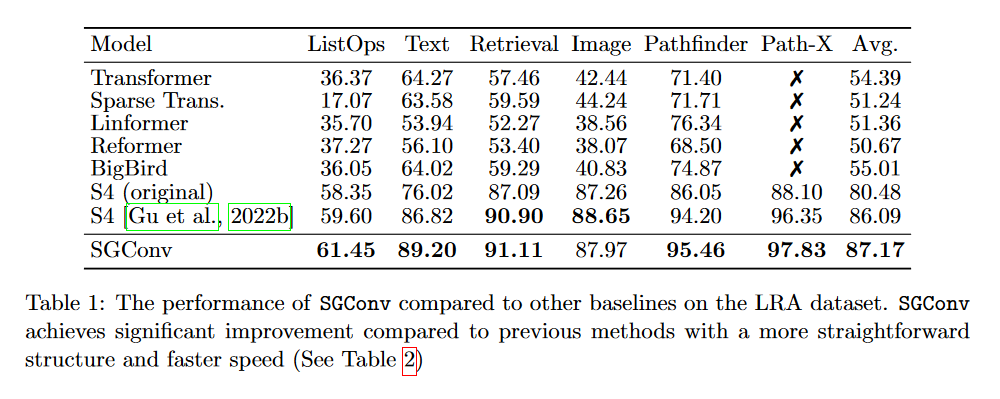
SGConv 作者报告称,在多项任务(文本、音频、图像)上取得了比 S4 更好的结果。我们在此不赘述细节。只看 LRA 的结果:
图 24:SGConv 在 LRA 上的结果。
确实,从这张表格中我们可以看到 SGConv 的表现优于 S4 的两个版本。然而,令人好奇的是,作者没有将 Mega、Liquid-S4 或 S5 纳入比较,这些模型都通过使用由递减指数函数之和构成的卷积核取得了更好的结果。
最终,SGConv 的表现似乎与最新的 SSM 变体相似,但失去了 S4 的循环视图。
深入探讨 GitHub 上获取。Open Review 上的讨论。
其他模型
2022 年发表了另外两篇“理论”论文:WANG 等人引入 BiGS 的 Pretraining Without Attention Hungry Hungry Hippos: Towards Language Modeling with State Space Models
SSM 应用
SaShiMi
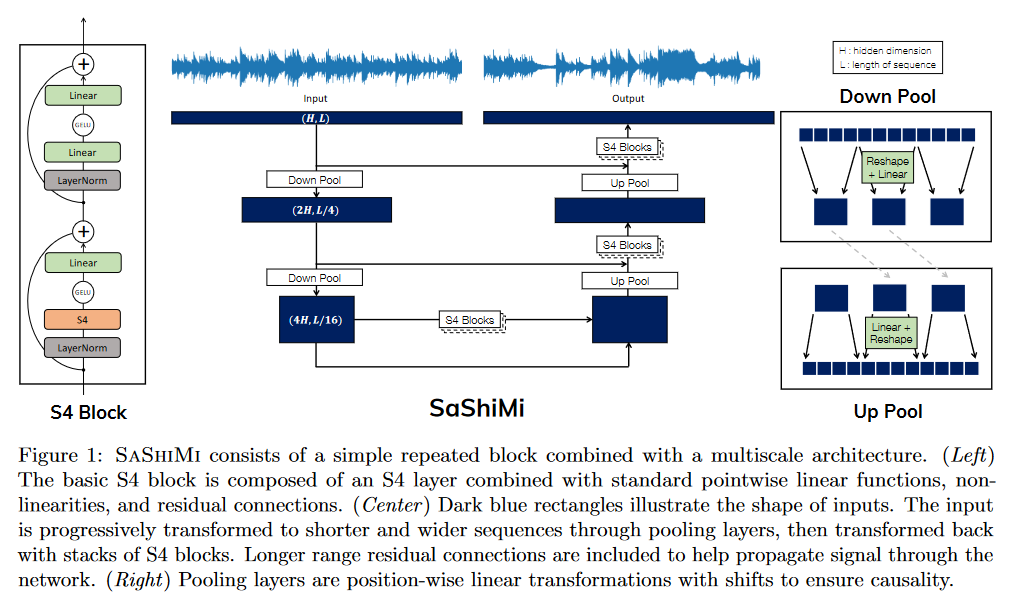
在 2022 年 2 月 20 日发表的论文 It's Raw! Audio Generation with State-Space Models WaveNet 进行比较。https://hazyresearch.stanford.edu/sashimi-examples/ 。
图 25:Sashimi 架构概述
深入探讨 GitHub 上获取。
ViS4mer
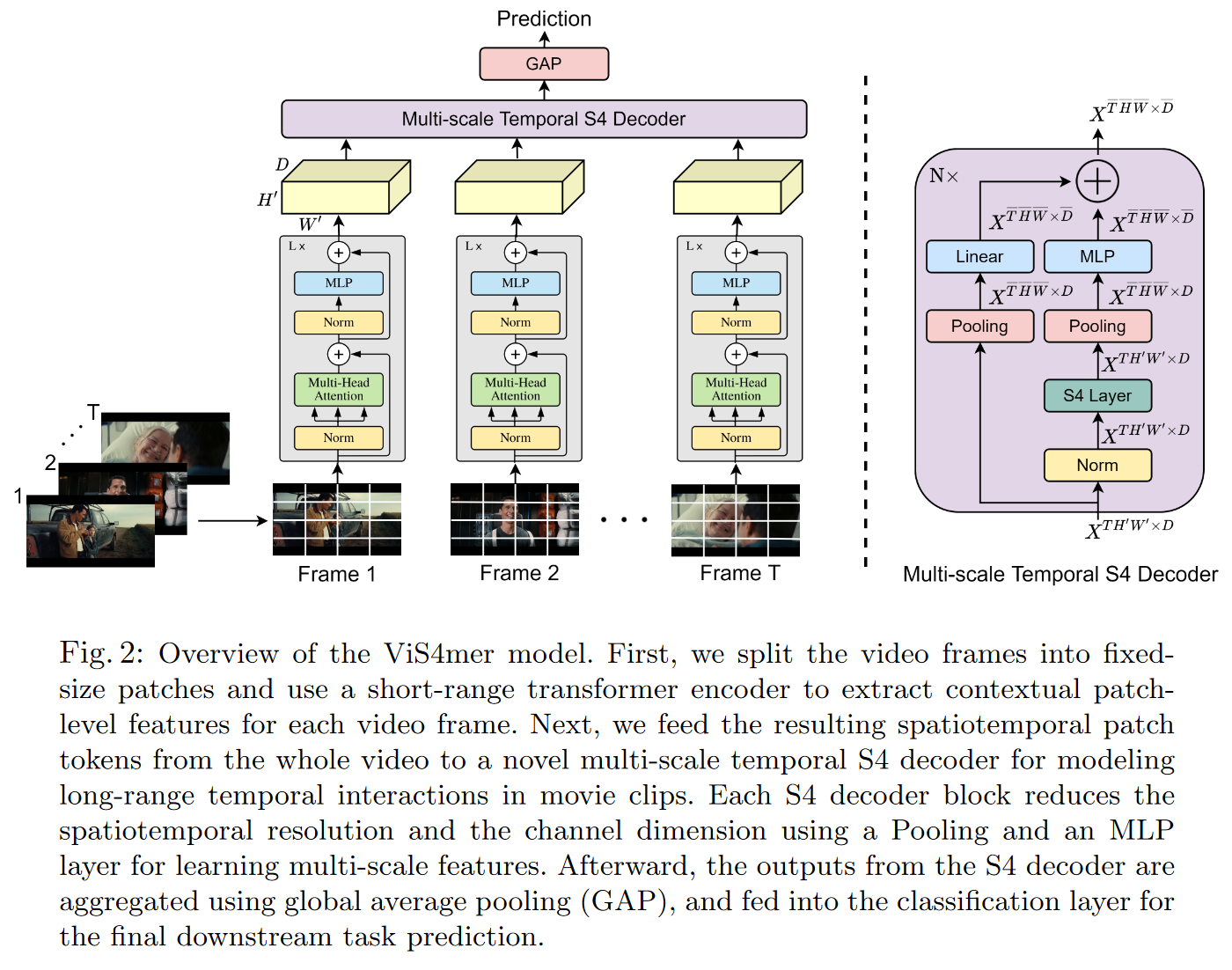
2022 年 4 月 4 日,ISLAM 和 BERTASIUS 在他们的论文 Long Movie Clip Classification with State-Space Video Models
图 26:ViS4mer 解码器概述
ViS4mer 在 WU 和 KRÄHENBÜHL (2021) 的基准测试 Long Video Understanding
深入探讨 GitHub 上获取。
CCNN
2022 年 6 月 7 日,ROMERO、KNIGGE 等人在他们的论文 Towards a General Purpose CNN for Long Range Dependencies in ND
输入长度:32x32,1024x1024 → 如何建模长程依赖?
输入分辨率:8kHz,16kHz → 长程依赖,分辨率无关性?
输入维度:1D,2D,3D → 如何定义卷积核?
任务:分类、分割等 → 如何定义高低采样策略?
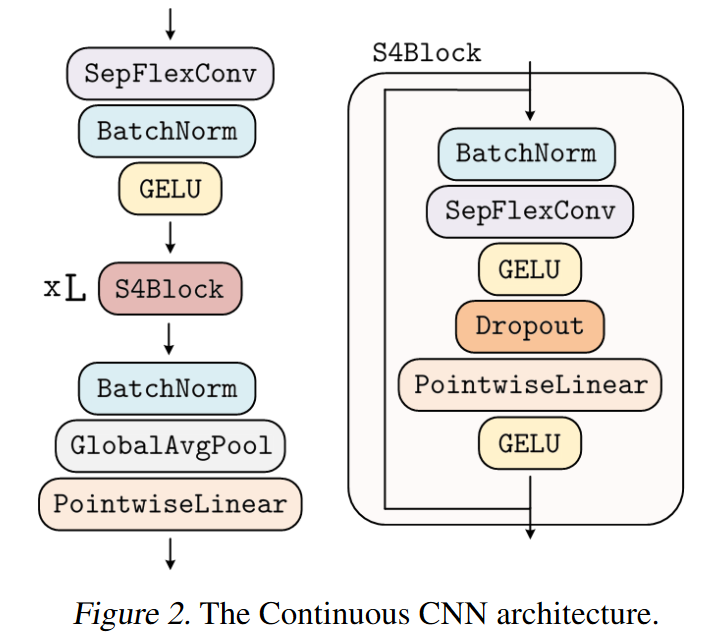
ROMERO、KNIGGE 等人从 S4 中汲取灵感,创建了一种高效残差块的变体,他们称之为 S4 块 。然而,与仅适用于 1D 信号的 S4 不同,CCNN 可以轻松建模 ND 信号。
图 27:CCNN 概述
深入探讨 GitHub 上获取。https://app.slidebean.com/sbp/gk5j826nq7/CCNN#1
S S S D S 4 SSS D S4
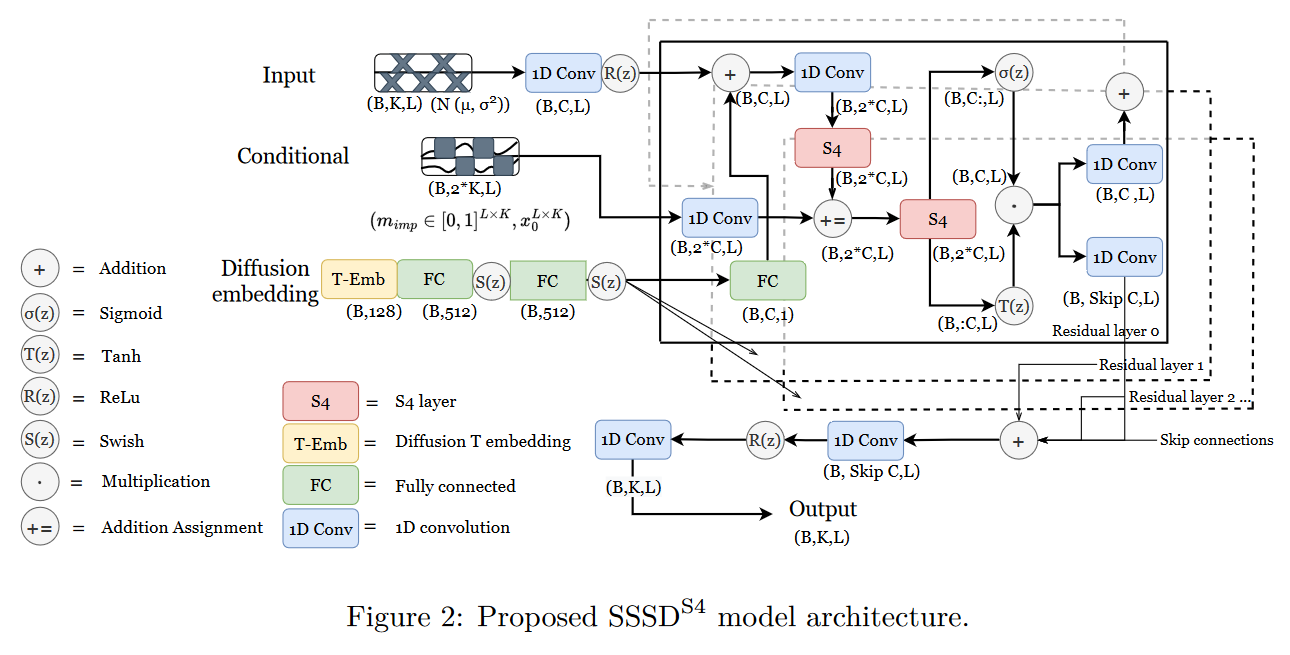
2022 年 8 月 19 日,LOPEZ ALCARAZ 和 STRODTHOFF 在其论文 Diffusion-based Time Series Imputation and Forecasting with Structured State Space Models S S S D S 4 SSS D S4
图 28:SSSD 概述
深入探讨 GitHub 上获取。
S4ND
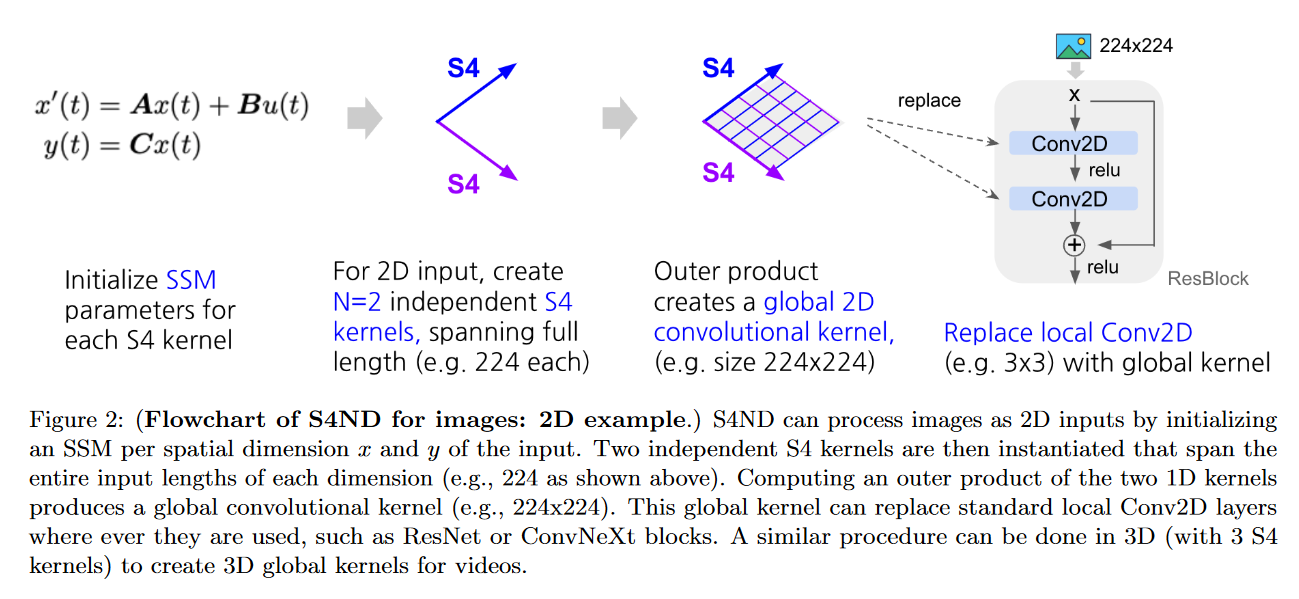
2022 年 10 月 12 日,NGUYEN、GOEL、GU 等人提出了 S4ND: Modeling Images and Videos as Multidimensional Signals Using State Spaces
该模型将 S4(1D)扩展到多维连续信号,如图像和视频(而 ConvNets 和 ViT 在离散像素上学习)。为此,他们将标准 S4 ODE 转换为多维 PDE:
x ′ ( t ) = A x ( t ) + B u ( t ) y ( t ) = C x ( t ) x ′ ( t ) y ( t ) = A x ( t ) + B u ( t ) = C x ( t )
变为
∂ ∂ t ( 1 ) x ( t ( 1 ) , t ( 2 ) ) = ( A ( 1 ) x ( 1 ) ( t ( 1 ) , t ( 2 ) ) , x ( 2 ) ( t ( 1 ) , t ( 2 ) ) ) + B ( 1 ) u ( t ( 1 ) , t ( 2 ) ) ∂ ∂ t ( 2 ) x ( t ( 1 ) , t ( 2 ) ) = ( x ( 1 ) ( t ( 1 ) , t ( 2 ) ) , A ( 2 ) x ( 2 ) ( t ( 1 ) , t ( 2 ) ) ) + B ( 2 ) u ( t ( 1 ) , t ( 2 ) ) y ( t ( 1 ) , t ( 2 ) ) = ⟨ C , x ( t ( 1 ) , t ( 2 ) ) ⟩ ∂ t ( 1 ) ∂ x ( t ( 1 ) , t ( 2 ) ) ∂ t ( 2 ) ∂ x ( t ( 1 ) , t ( 2 ) ) y ( t ( 1 ) , t ( 2 ) ) = ( A ( 1 ) x ( 1 ) ( t ( 1 ) , t ( 2 ) ) , x ( 2 ) ( t ( 1 ) , t ( 2 ) )) + B ( 1 ) u ( t ( 1 ) , t ( 2 ) ) = ( x ( 1 ) ( t ( 1 ) , t ( 2 ) ) , A ( 2 ) x ( 2 ) ( t ( 1 ) , t ( 2 ) )) + B ( 2 ) u ( t ( 1 ) , t ( 2 ) ) = ⟨ C , x ( t ( 1 ) , t ( 2 ) )⟩
其中 A ( τ ) ∈ C N ( τ ) × N ( τ ) A ( τ ) ∈ C N ( τ ) × N ( τ ) B ( τ ) ∈ C N ( τ ) × 1 B ( τ ) ∈ C N ( τ ) × 1 C ∈ C N ( 1 ) × N ( 2 ) C ∈ C N ( 1 ) × N ( 2 ) x ( 0 , 0 ) = 0 x ( 0 , 0 ) = 0
根据所测试的数据集,作者获得了与ViT或ConvNext相似或更好的结果。
在零样本情况下,S4ND 在 8 × 8 8 × 8 32 × 32 32 × 32
通过渐进式尺寸调整,S4ND 可以将训练速度提高 22%,而最终准确度与仅在高分辨率下训练相比下降约 1%。
图 30:S4ND 在 2D 图像中的示例
深入探讨 GitHub 上获取。Darude S4NDstorm 。
结论
因此,我们回顾了 2022 年发布的各种 SSM 模型。在这一年中,主要工作集中于通过各种方法(对角化、门控、LTC 等)改进/简化 S4。2022 年也首次出现了 SSM 的应用。
参考文献
结合循环、卷积和连续时间模型的线性状态空间层 ,作者:Albert GU, Isys JOHNSON, Karan GOEL, Khaled SAAB, Tri DAO, Atri RUDRA, Christopher RÉ (2021)使用结构化状态空间高效建模长序列 ,作者:Albert GU, Karan GOEL, et Christopher RÉ (2021)HiPPO:具有最优多项式投影的循环记忆 ,作者:Albert GU, Tri DAO, Stefano ERMON, Atri RUDRA, Christopher RÉ (2020)如何训练你的HiPPO 长程竞技场:高效Transformer基准 对角状态空间与结构化状态空间同样有效 语音指令:有限词汇语音识别数据集 使用对角线性RNN简化和理解状态空间模型 关于对角状态空间模型的参数化和初始化 通过门控状态空间进行长程语言建模 使用门控卷积网络进行语言建模 GLU变体改进Transformer 线性时间内的Transformer质量 Mega:配备移动平均的门控注意力 液体结构状态空间模型 液体时间常数网络 简化状态空间层用于序列建模 从脉搏血氧仪稳健估计呼吸频率 什么让卷积模型在长序列建模上表现出色? 无注意力的预训练 饥饿的河马:走向状态空间模型的语言建模 原始音频!使用状态空间模型生成音频 WaveNet:原始音频的生成模型 使用状态空间视频模型进行长电影片段分类 长视频理解 为ND中长程依赖性而设计的通用CNN 基于扩散的时间序列插值和预测与结构化状态空间模型 S4ND:使用状态空间将图像和视频建模为多维信号
引用
@inproceedings{ssm_in_2022_blog_post,https://lbourdois.github.io/blog/ssm/ssm_en_2022}