用积分微分方程建模AdaGrad、RMSProp和Adam

概述

• 研究探讨了自适应优化算法的连续时间模型
• 重点关注AdaGrad、RMSProp和Adam优化器
• 开发了积分微分方程来模拟优化器的行为
• 证明了各种优化场景下的收敛特性
• 展示了离散和连续优化方法之间的联系

通俗易懂的解释

优化算法帮助机器学习模型高效学习。这项研究探讨了三种流行的优化方法——AdaGrad、RMSProp和Adam——的核心工作原理。可以将这些优化器想象成不同的登山策略——每种策略都有自己决定路径的方式。

研究人员创建了数学模型，展示了这些算法如何随时间变化，类似于物理学家模拟物体运动的方式。通过将分步的计算机算法转换为平滑的连续数学方程，他们对这些方法为何有效有了新的见解。

这种方法揭示了优化器如何调整其学习过程，就像徒步旅行者根据地形改变步伐一样。连续模型有助于解释为什么某些优化器在不同情况下表现更好。

主要发现

研究表明

• 自适应优化方法可以用连续数学精确建模
• 连续模型可以预测优化器在简单和复杂场景中的行为
• 每个优化器都有独特的收敛特性，与实际观察结果相符
• 该数学框架为分析优化算法提供了新工具

技术解释

本研究开发了积分微分方程，用于捕捉自适应优化方法的行为。这些方程模拟了优化器如何随时间积累和使用梯度信息。

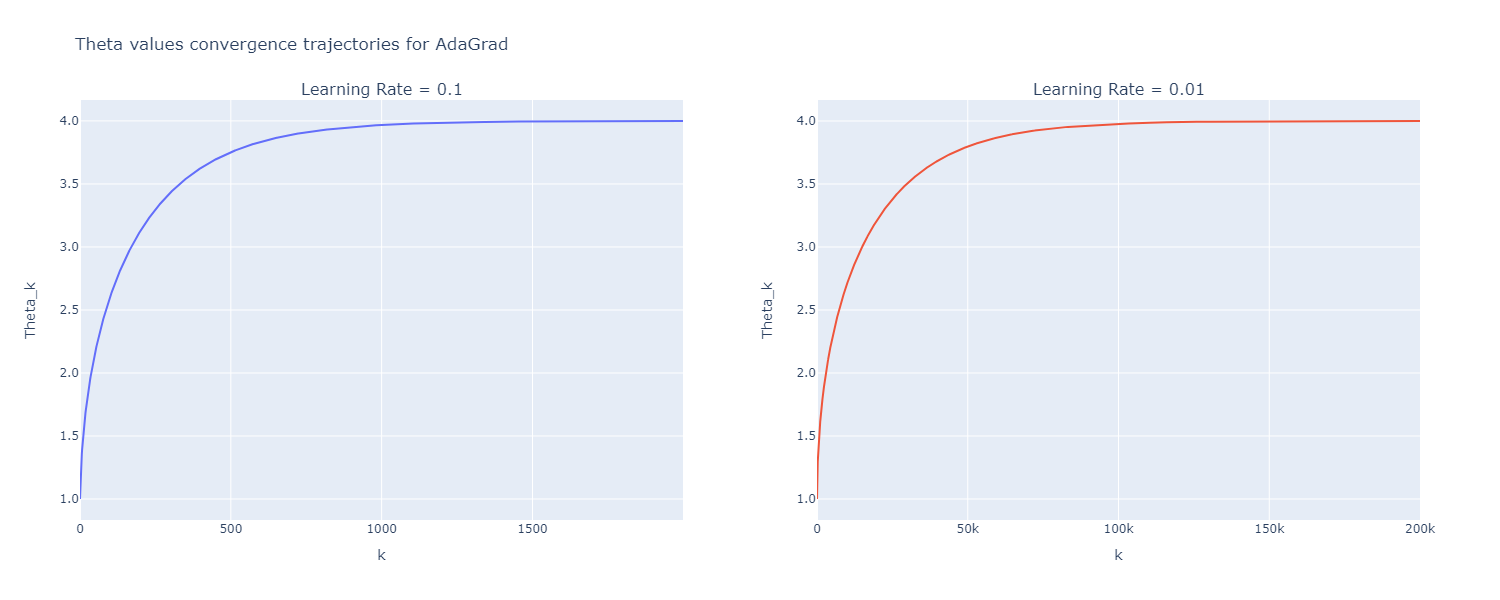
连续时间分析表明，AdaGrad的自适应机制导致步长自然减小，而RMSProp和Adam通过指数平均保持更一致的步长。

该数学框架为收敛速度和稳定性特性提供了严格的证明，与实际应用中的经验观察相符。

批判性分析

本研究的局限性包括

• 模型假设的理想条件可能与现实场景不符
• 分析侧重于理论方面而非实际实现
• 某些数学假设在深度学习应用中可能不成立

未来的研究可以探索

• 扩展到更复杂的优化环境
• 优化器设计的实际意义
• 与其他优化方法的联系

结论

这项研究弥合了离散优化算法与连续数学之间的鸿沟。获得的见解有助于开发更好的优化方法和更深入地理解现有算法。这项工作为分析和改进机器学习优化技术开辟了新途径。

该数学框架为优化理论和实际算法设计的未来研究奠定了基础。这些进步有助于为机器学习模型开发更高效的训练方法。