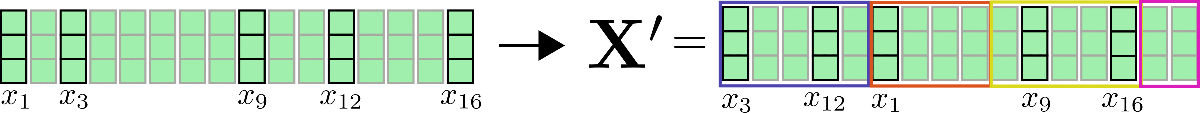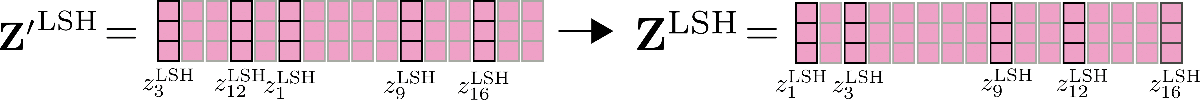Reformer——突破语言模型限制

Patrick von Platen

patrickvonplaten

关注

Reformer 如何使用不到 8GB 内存训练 50 万个词元的序列

由 Kitaev、Kaiser 等人 (2020) 提出的 Reformer 模型是目前用于长序列建模的最节省内存的 Transformer 模型之一。

最近，长序列建模引起了广泛关注，仅今年就有许多相关提交，例如 Beltagy 等人 (2020)、Roy 等人 (2020)、Tay 等人、Wang 等人。长序列建模的动机是，NLP 中的许多任务，例如摘要、问答，要求模型处理比 BERT 等模型能够处理的更长的输入序列。在需要模型处理大型输入序列的任务中，长序列模型无需截断输入序列以避免内存溢出，因此已被证明优于标准“BERT”类模型，参见 Beltagy 等人 (2020)。

Reformer 通过其一次处理多达 50 万个词元的能力（如本演示所示），将长序列建模的极限推向了新的高度。相比之下，传统的 bert-base-uncased 模型将输入长度限制为仅 512 个词元。在 Reformer 中，标准 Transformer 架构的每个部分都经过重新设计，以优化最小内存需求，同时性能没有显著下降。

内存改进可归因于 Reformer 作者引入 Transformer 领域的 4 个特性

1. Reformer 自注意力层 - 如何在不受本地上下文限制的情况下高效实现自注意力？
2. 分块前馈层 - 如何为大型前馈层获得更好的时间-内存权衡？
3. 可逆残差层 - 如何通过巧妙的残差架构大幅减少训练中的内存消耗？
4. 轴向位置编码 - 如何使位置编码适用于极长输入序列？

本博客文章的目标是让读者深入了解上述四个 Reformer 特性。虽然解释侧重于 Reformer，但读者应该能更好地理解这四个特性在何种情况下对其他 Transformer 模型也有效。这四个部分之间只有松散的联系，因此可以独立阅读。

Reformer 是 🤗Transformers 库的一部分。对于所有 Reformer 用户，建议仔细阅读这篇非常详细的博客文章，以便更好地理解模型的工作原理以及如何正确设置其配置。所有公式都附有其在 Reformer 配置中的等效名称，例如 config.，以便读者可以快速查阅官方文档和配置文件。

注意：官方 Reformer 论文中没有解释轴向位置编码，但它们在官方代码库中被广泛使用。本博客文章首次深入解释了轴向位置编码。

1. Reformer 自注意力层

Reformer 使用两种特殊的自注意力层：局部自注意力层和局部敏感哈希 (LSH) 自注意力层。

为了更好地介绍这些新的自注意力层，我们将简要回顾 Vaswani 等人 2017 中介绍的传统自注意力。

本博客文章使用与流行博客文章 The illustrated transformer 相同的符号和颜色，因此强烈建议读者首先阅读该博客。

重要：Reformer 最初是为因果自注意力引入的，但它也可以很好地用于双向自注意力。在这篇文章中，Reformer 的自注意力以双向自注意力的形式呈现。

全局自注意力回顾

每个 Transformer 模型的核心是自注意力层。为了回顾传统的自注意力层（这里我们称之为全局自注意力层），我们假设将 Transformer 层应用于嵌入向量序列 $\mathbf{X} = \mathbf{x}_1, \ldots, \mathbf{x}_n$，其中每个向量 $\mathbf{x}_{i}$ 的大小为 config.hidden_size，即 $d_h$。

简而言之，全局自注意力层将 $\mathbf{X}$ 投影到查询、键和值矩阵 $\mathbf{Q}, \mathbf{K}, \mathbf{V}$，并使用 softmax 运算计算输出 $\mathbf{Z}$，如下所示：$\mathbf{Z} = \text{SelfAttn}(\mathbf{X}) = \text{softmax}(\mathbf{Q}\mathbf{K}^T) \mathbf{V}$，其中 $\mathbf{Z}$ 的维度为 $d_h \times n$（为简化起见，省略了键归一化因子和自注意力权重 $\mathbf{W}^{O}$）。有关完整 Transformer 操作的更多详细信息，请参阅 The illustrated transformer。

在可视化方面，我们可以将此操作说明如下，其中 $n=16, d_h=3$

请注意，对于所有可视化，batch_size 和 config.num_attention_heads 都假定为 1。某些向量，例如 $\mathbf{x_3}$ 及其对应的输出向量 $\mathbf{z_3}$ 被标记，以便稍后更好地解释 LSH 自注意力。所呈现的逻辑可以毫不费力地扩展到多头自注意力（config.num_attention_{h}eads > 1）。建议读者阅读 The illustrated transformer 作为多头自注意力的参考。

重要的是要记住，对于每个输出向量 $\mathbf{z}_{i}$，处理了整个输入序列 $\mathbf{X}$。内积 $\mathbf{Q}\mathbf{K}^T$ 张量的渐近内存复杂度为 $\mathcal{O}(n^2)$，这通常是 Transformer 模型中的内存瓶颈。

这也是 bert-base-cased 的 config.max_position_embedding_size 仅为 512 的原因。

局部自注意力

局部自注意力是减少 $\mathcal{O}(n^2)$ 内存瓶颈的显而易见的解决方案，它允许我们以降低的计算成本对更长的序列进行建模。在局部自注意力中，输入 $\mathbf{X} = \mathbf{X}_{1:n} = \mathbf{x}_{1}, \ldots, \mathbf{x}_{n}$ 被切成 $n_{c}$ 个块：$\mathbf{X} = \left[\mathbf{X}_{1:l_{c}}, \ldots, \mathbf{X}_{(n_{c} - 1) * l_{c} : n_{c} * l_{c}}\right]$，每个块的长度为 config.local_chunk_length，即 $l_{c}$，然后对每个块分别应用全局自注意力。

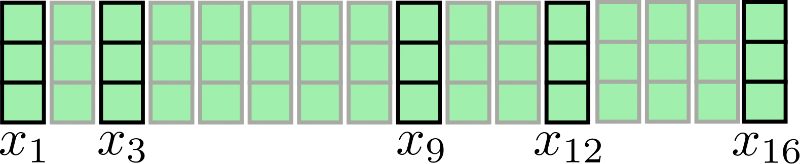
让我们再次以 $n=16, d_h=3$ 的输入序列为例进行可视化

假设 $l_{c} = 4, n_{c} = 4$4，分块注意力可以可视化如下

正如所见，注意力操作分别应用于每个块 $\mathbf{X}_{1:4}, \mathbf{X}_{5:8}, \mathbf{X}_{9:12}, \mathbf{X}_{13:16}$。这种架构的第一个缺点显而易见：某些输入向量无法访问其直接上下文，例如在我们的示例中，$\mathbf{x}_9$ 无法访问 $\mathbf{x}_{8}$，反之亦然。这很成问题，因为这些词元无法学习考虑到其直接上下文的词表示。

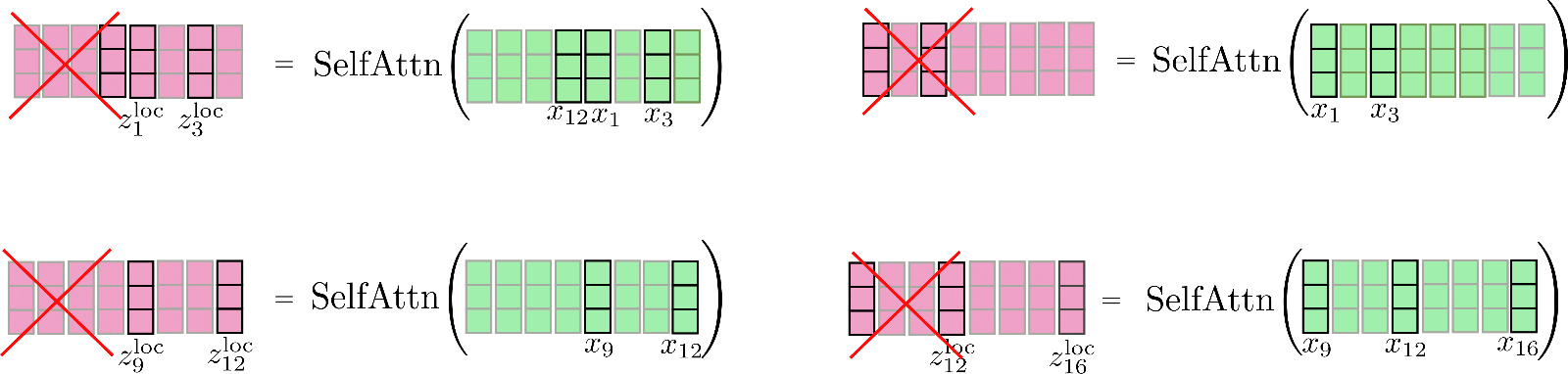
一个简单的补救措施是为每个块增加 config.local_num_chunks_before，即 $n_{p}$ 个块，以及 config.local_num_chunks_after，即 $n_{a}$ 个块，这样每个输入向量至少可以访问 $n_{p}$ 个先前的输入向量和 $n_{a}$ 个后续输入向量。这也可以理解为具有重叠的分块，其中 $n_{p}$ 和 $n_{a}$ 定义了每个块与所有先前块和后续块的重叠量。我们将这种扩展的局部自注意力表示为

$$\mathbf{Z}^{\text{loc}} = \left[\mathbf{Z}_{1:l_{c}}^{\text{loc}}, \ldots, \mathbf{Z}_{(n_{c} - 1) * l_{c} : n_{c} * l_{c}}^{\text{loc}}\right],$$loc​], 其中 $$\mathbf{Z}_{l_{c} * (i - 1) + 1 : l_{c} * i}^{\text{loc}} = \text{SelfAttn}(\mathbf{X}_{l_{c} * (i - 1 - n_{p}) + 1: l_{c} * (i + n_{a})})\left[n_{p} * l_{c}: -n_{a} * l_{c}\right], \forall i \in \{1, \ldots, n_{c} \}$$=SelfAttn(Xlc​∗(i−1−np​)+1:lc​∗(i+na​)​)[np​∗lc​:−na​∗lc​],∀i∈{1,…,nc​}

好的，这个公式看起来很复杂。让我们简化它。在 Reformer 的自注意力层中，$n_{a}$ 通常设置为 0，$n_{p}$ 设置为 1，因此让我们再次写下 $i = 1$ 的公式

$$\mathbf{Z}_{1:l_{c}}^{\text{loc}} = \text{SelfAttn}(\mathbf{X}_{-l_{c} + 1: l_{c}})\left[l_{c}:\right]$$=SelfAttn(X−lc​+1:lc​​)[lc​:]

我们注意到存在循环关系，因此第一个段也可以关注最后一个段。让我们再次说明这种略微增强的局部注意力。首先，我们在每个窗口化段内应用自注意力，并只保留中心输出段。

最后，将相关输出连接到 $\mathbf{Z}^{\text{loc}}$，其结果如下所示。

请注意，局部自注意力是以高效方式实现的，因此不会像此处为说明目的而用红叉表示的那样计算并随后“丢弃”任何输出。

这里需要注意的是，扩展每个分块自注意力函数的输入向量可以使每个单一输出向量$\mathbf{z}_{i}$更好地学习向量表示。例如，输出向量$\mathbf{z}_{5}^{\text{loc}}, \mathbf{z}_{6}^{\text{loc}}, \mathbf{z}_{7}^{\text{loc}}, \mathbf{z}_{8}^{\text{loc}}$都可以考虑所有输入向量$\mathbf{X}_{1:8}$来学习更好的表示。

内存消耗的增长显而易见：$\mathcal{O}(n^2)$的内存复杂度被分解为每个段单独处理，从而将总渐近内存消耗降低到$\mathcal{O}(n_{c} * l_{c}^2) = \mathcal{O}(n * l_{c})$。

这种增强的局部自注意力优于普通的局部自注意力架构，但仍然存在一个主要缺点，即每个输入向量只能关注预定义大小的局部上下文。对于不需要Transformer模型学习输入向量之间长距离依赖关系的NLP任务（其中可能包括语音识别、命名实体识别和短句子因果语言建模），这可能不是一个大问题。许多NLP任务确实需要模型学习长距离依赖关系，因此局部自注意力可能导致显著的性能下降，例如：

• 问答：模型必须学习问题标记和相关答案标记之间的关系，这些标记很可能不在同一个局部范围内。
• 多项选择：模型必须比较多个答案标记段，这些段通常由显著的长度分隔。
• 摘要：模型必须学习长序列上下文标记和短序列摘要标记之间的关系，而上下文和摘要之间的相关关系很可能无法通过局部自注意力捕获。
• 等等...

局部自注意力本身很可能不足以让Transformer模型学习输入向量（标记）之间的相关关系。

因此，Reformer还采用了近似全局自注意力的有效自注意力层，称为LSH自注意力。

LSH自注意力

好了，既然我们已经了解了局部自注意力是如何工作的，我们就可以尝试Reformer中最具创新性的部分：局部敏感哈希（LSH）自注意力。

LSH自注意力前提是效率或多或少与局部自注意力相当，同时近似全局自注意力。

LSH自注意力依赖于Andoni等人（2015）中提出的LSH算法，因此得名。

LSH自注意力的思想基于一个洞察力：如果$n$很大，则应用于$\mathbf{Q}\mathbf{K}^T$注意力点积权重上的softmax函数对于每个查询向量只有少数值明显大于0。

我们来详细解释一下。设$\mathbf{k}_{i} \in \mathbf{K} = \left[\mathbf{k}_1, \ldots, \mathbf{k}_n \right]^T$和$\mathbf{q}_{i} \in \mathbf{Q} = \left[\mathbf{q}_1, \ldots, \mathbf{q}_n\right]^T$为键向量和查询向量。对于每个$\mathbf{q}_{i}$，计算$\text{softmax}(\mathbf{q}_{i}^T \mathbf{K}^T)$可以通过仅使用与$\mathbf{q}_{i}$具有高余弦相似度的键向量$\mathbf{k}_{j}$来近似。这是因为softmax函数对较大的输入值赋予指数级更多的权重。到目前为止一切顺利，下一个问题是高效地找到与所有$i$的$\mathbf{q}_{i}$具有高余弦相似度的向量。

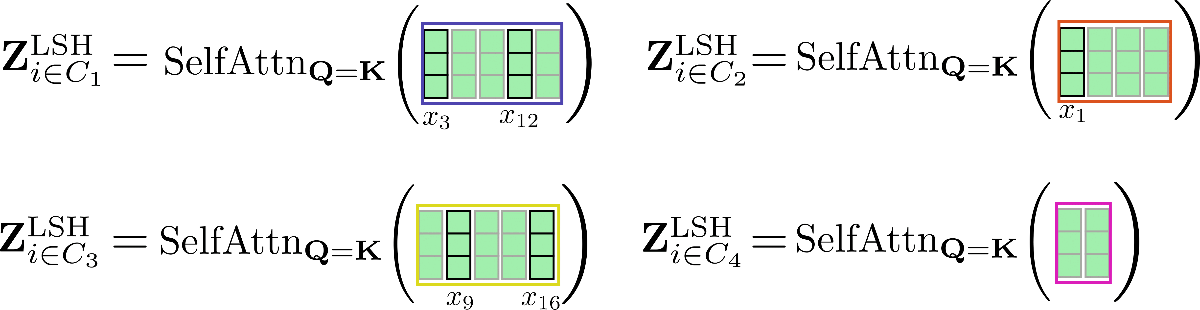
首先，Reformer的作者注意到共享查询和键投影：$\mathbf{Q} = \mathbf{K}$不会影响Transformer模型的性能${}^1$。现在，不再需要为每个查询向量$q_i$查找具有高余弦相似度的键向量，只需要找到查询向量彼此之间的余弦相似度。这很重要，因为查询-查询向量点积近似具有传递性：如果$\mathbf{q}_{i}$与查询向量$\mathbf{q}_{j}$和$\mathbf{q}_{k}$具有高余弦相似度，那么$\mathbf{q}_{j}$也与$\mathbf{q}_{k}$具有高余弦相似度。因此，查询向量可以被聚类到桶中，使得属于同一桶的所有查询向量彼此之间具有高余弦相似度。我们定义$C_{m}$为第m组位置索引，使得其对应的查询向量在同一桶中：$C_{m} = \{ i | \text{ s.t. } \mathbf{q}_{i} \in \text{mth cluster}\}$和config.num_buckets，即$n_{b}$，为桶的数量。

对于每组索引$C_{m}$，在相应查询向量桶上的softmax函数$\text{softmax}(\mathbf{Q}_{i \in C_{m}} \mathbf{Q}^T_{i \in C_{m}})$近似了共享查询和键投影的全局自注意力函数$\text{softmax}(\mathbf{q}_{i}^T \mathbf{Q}^T)$，适用于$C_{m}$中所有位置索引$i$。

其次，作者利用LSH算法将查询向量聚类到预定义数量的桶$n_{b}$中。LSH算法是理想的选择，因为它非常高效，并且是余弦相似度最近邻算法的近似。本笔记本不讨论LSH方案，因此我们只需记住，对于每个向量$\mathbf{q}_{i}$，LSH算法将其位置索引$i$归因于$n_{b}$个预定义桶中的一个，即$\text{LSH}(\mathbf{q}_{i}) = m$，其中$i \in \{1, \ldots, n\}$和$m \in \{1, \ldots, n_{b}\}$。

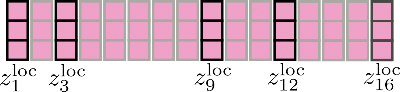
在视觉上，我们可以用我们的原始示例来阐述这一点：

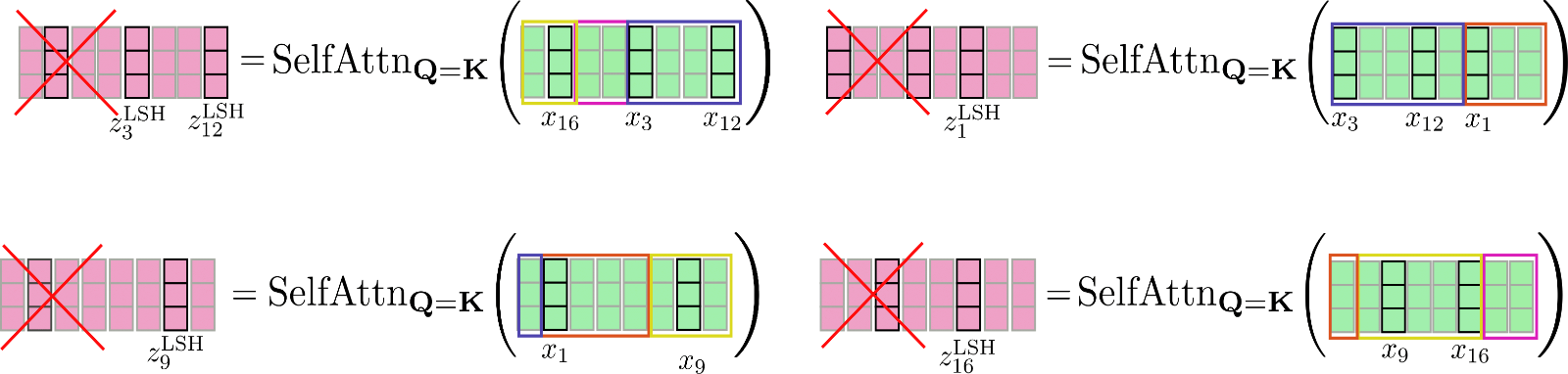
第三，需要注意的是，在将所有查询向量聚类到$n_{b}$个桶中之后，相应的索引集$C_{m}$可以用来相应地置换输入向量$\mathbf{x}_1, \ldots, \mathbf{x}_n$${}^2$，以便可以像局部注意力一样分段应用共享查询键自注意力。

我们再用我们的示例输入向量$\mathbf{X} = \mathbf{x}_1, ..., \mathbf{x}_{16}$进行阐述，假设config.num_buckets=4和config.lsh_chunk_length = 4。看上面的图，我们可以看到我们已经将每个查询向量$\mathbf{q}_1, \ldots, \mathbf{q}_{16}$分配到其中一个集群$\mathcal{C}_{1}, \mathcal{C}_{2}, \mathcal{C}_{3}, \mathcal{C}_{4}$。如果现在我们将相应的输入向量$\mathbf{x}_1, \ldots, \mathbf{x}_{16}$进行排序，我们将得到以下置换后的输入$\mathbf{X'}$

自注意力机制应该独立地应用于每个集群，以便对于每个集群$\mathcal{C}_m$，其相应的输出计算如下：$\mathbf{Z}^{\text{LSH}}_{i \in \mathcal{C}_m} = \text{SelfAttn}_{\mathbf{Q}=\mathbf{K}}(\mathbf{X}_{i \in \mathcal{C}_m})$。

我们再用这个例子来解释一下。

可以看出，自注意力函数操作于不同大小的矩阵，这对于GPU和TPU中的高效批处理来说并不理想。

为了解决这个问题，可以像局部注意力一样对置换后的输入进行分块，使得每个块的大小为config.lsh_chunk_length。通过对置换后的输入进行分块，一个桶可能会被分成两个不同的块。为了解决这个问题，在LSH自注意力中，每个块除了关注自身之外，还会关注其前一个块config.lsh_num_chunks_before=1，这与局部自注意力的方式相同（config.lsh_num_chunks_after通常设置为0）。通过这种方式，我们可以确保一个桶中的所有向量以高概率相互关注${}^3$。

总而言之，对于所有块$k \in \{1, \ldots, n_{c}\}$，LSH自注意力可以记作如下

$$\mathbf{Z'}_{l_{c} * k + 1:l_{c} * (k + 1)}^{\text{LSH}} = \text{SelfAttn}_{\mathbf{Q} = \mathbf{K}}(\mathbf{X'}_{l_{c} * k + 1): l_{c} * (k + 1)})\left[l_{c}:\right]$$

其中 $\mathbf{X'}$ 和 $\mathbf{Z'}$ 是根据 LSH 算法排列的输入和输出向量。公式太复杂了，我们来演示一下 LSH 自注意力机制。

如上所示，排列后的向量 $\mathbf{X'}$ 被分块，并且共享查询键的自注意力机制被应用于每个块。

最后，输出 $\mathbf{Z'}^{\text{LSH}}$ 被重新排序为原始排列。

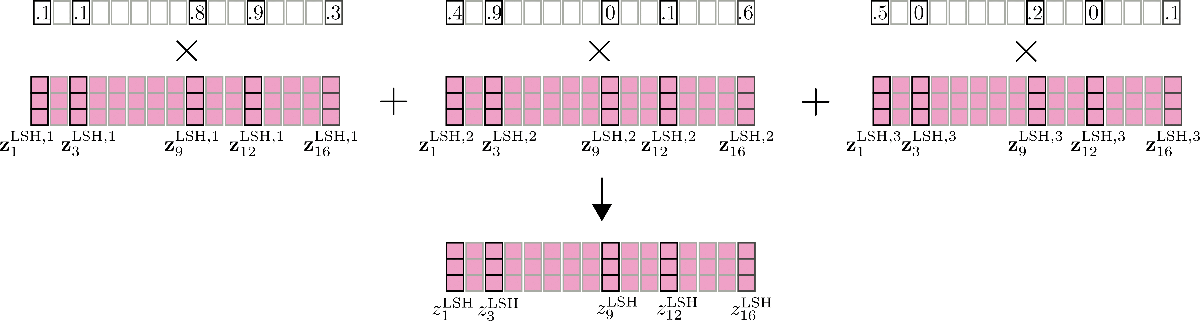
这里还要提到一个重要特性：LSH 自注意力的准确性可以通过并行运行 LSH 自注意力 `config.num_hashes` 次（例如 $n_{h}$ 次），每次使用不同的随机 LSH 哈希来提高。通过设置 `config.num_hashes > 1`，对于每个输出位置 $i$，计算并随后合并多个输出向量：$\mathbf{z}^{\text{LSH}, 1}_{i}, \ldots, \mathbf{z}^{\text{LSH}, n_{h}}_{i}$，然后合并：$\mathbf{z}^{\text{LSH}}_{i} = \sum_k^{n_{h}} \mathbf{Z}^{\text{LSH}, k}_{i} * \text{weight}^k_i$。其中 $\text{weight}^k_i$ 表示哈希轮次 $k$ 的输出向量 $\mathbf{z}^{\text{LSH}, k}_{i}$ 相对于其他哈希轮次的重要性，并且与它们的 softmax 计算的归一化项呈指数比例。这背后的直觉是，如果相应的查询向量 $\mathbf{q}_{i}^{k}$ 与其所在块中的所有其他查询向量具有高度的余弦相似性，那么该块的 softmax 归一化项往往会很高，因此相应的输出向量 $\mathbf{q}_{i}^{k}$ 应该能更好地近似全局注意力，因此比 softmax 归一化项较低的哈希轮次的输出向量获得更多权重。更多详情请参阅论文附录 A。对于我们的示例，多轮 LSH 自注意力可以如下所示。

太棒了。就是这样。现在我们知道 Reformer 中 LSH 自注意力是如何工作的了。

关于内存复杂度，我们现在有两个术语相互竞争，成为内存瓶颈：点积：$\mathcal{O}(n_{h} * n_{c} * l_{c}^2) = \mathcal{O}(n * n_{h} * l_{c})$ 和 LSH 分桶所需的内存：$\mathcal{O}(n * n_{h} * \frac{n_{b}}{2})$，其中 $l_{c}$ 是块长度。因为对于大的 $n$，桶的数量 $\frac{n_{b}}{2}$ 比块长度 $l_{c}$ 增长得更快，用户可以再次对桶的数量 `config.num_buckets` 进行因式分解，如此处所述。

让我们快速回顾一下上面所讲的内容

1. 我们希望利用 softmax 操作仅将显著权重分配给极少数键向量的知识来近似全局注意力。
2. 如果键向量等于查询向量，这意味着*对于每个*查询向量 $\mathbf{q}_{i}$，softmax 只会将显著权重分配给在余弦相似度方面相似的其他查询向量。
3. 这种关系是双向的，这意味着如果 $\mathbf{q}_{j}$ 与 $\mathbf{q}_{i}$ 相似，那么 $\mathbf{q}_{j}$ 也与 $\mathbf{q}_{i}$ 相似，因此我们可以在对排列的输入应用自注意力之前进行全局聚类。
4. 我们将局部自注意力应用于排列后的输入，然后将输出重新排序为原始排列。

${}^{1}$ 作者进行了一些初步实验，证实共享查询键自注意力与标准自注意力表现或多或少一样好。

${}^{2}$ 更准确地说，桶内的查询向量根据其原始顺序进行排序。这意味着如果，*例如*，向量 $\mathbf{q}_1, \mathbf{q}_3, \mathbf{q}_7$,q7​ 都被哈希到桶 2，那么桶 2 中向量的顺序仍然是 $\mathbf{q}_1$，然后是 $\mathbf{q}_3$ 和 $\mathbf{q}_7$。

${}^3$ 另外值得一提的是，作者对查询向量 $\mathbf{q}_{i}$ 进行了掩码处理，以防止向量注意自身。因为向量与自身的余弦相似度总是高于或等于与其他向量的余弦相似度，所以在共享查询键自注意力中，强烈不鼓励查询向量注意自身。

基准测试

基准测试工具最近已添加到 Transformers 中 - 详情请参阅此处。

为了展示使用“局部”+“LSH”自注意力可以节省多少内存，Reformer 模型 `google/reformer-enwik8` 在不同的 `local_attn_chunk_length` 和 `lsh_attn_chunk_length` 下进行了基准测试。`google/reformer-enwik8` 模型的默认配置和用法可以在此处查看更多详情。

首先，让我们进行一些必要的导入和安装。

#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml

from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments

首先，让我们使用*全局*自注意力来测试 Reformer 模型的内存使用情况。这可以通过设置 `lsh_attn_chunk_length` = `local_attn_chunk_length` = 8192 来实现，这样对于所有小于或等于 8192 的输入序列，模型会自动切换到全局自注意力。

config = ReformerConfig.from_pretrained("google/reformer-enwik8", lsh_attn_chunk_length=16386, local_attn_chunk_length=16386, lsh_num_chunks_before=0, local_num_chunks_before=0)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[2048, 4096, 8192, 16386], batch_sizes=[1], models=["Reformer"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config], args=benchmark_args)
result = benchmark.run()

HBox(children=(FloatProgress(value=0.0, description='Downloading', max=1279.0, style=ProgressStyle(description…



1 / 1
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 8.87 GiB already allocated; 1.92 GiB free; 8.88 GiB reserved in total by PyTorch)

====================      INFERENCE - MEMORY - RESULT       ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
           Reformer                  1              2048            1465     
           Reformer                  1              4096            2757     
           Reformer                  1              8192            7893     
           Reformer                  1             16386            N/A      
--------------------------------------------------------------------------------

输入序列越长，输入序列与峰值内存使用量之间的二次关系 $\mathcal{O}(n^2)$ 就越明显。可以看出，实际上需要更长的输入序列才能清楚地观察到输入序列翻倍，峰值内存使用量就会翻两番。

对于使用全局注意力的 `google/reformer-enwik8` 模型，序列长度超过 16K 会导致内存溢出。

现在，让我们通过使用模型的默认参数来激活*局部*和*LSH*自注意力。

  config = ReformerConfig.from_pretrained("google/reformer-enwik8")
  benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[2048, 4096, 8192, 16384, 32768, 65436], batch_sizes=[1], models=["Reformer"], no_speed=True, no_env_print=True)
  benchmark = PyTorchBenchmark(configs=[config], args=benchmark_args)
  result = benchmark.run()

1 / 1
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 7.85 GiB already allocated; 1.74 GiB free; 9.06 GiB reserved in total by PyTorch)
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 4.00 GiB (GPU 0; 11.17 GiB total capacity; 6.56 GiB already allocated; 3.99 GiB free; 6.81 GiB reserved in total by PyTorch)

====================      INFERENCE - MEMORY - RESULT       ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
           Reformer                  1              2048            1785     
           Reformer                  1              4096            2621     
           Reformer                  1              8192            4281     
           Reformer                  1             16384            7607     
           Reformer                  1             32768            N/A      
           Reformer                  1             65436            N/A      
--------------------------------------------------------------------------------

正如所料，使用局部和 LSH 自注意力对于较长的输入序列来说效率更高，因此在该笔记本中，模型仅在 16K 令牌的 11GB RAM GPU 上才耗尽内存。

2. 分块前馈层

基于 Transformer 的模型通常在自注意力层之后并行使用非常大的前馈层。因此，该层会占用大量总内存，有时甚至成为模型的内存瓶颈。前馈分块技术首次在 Reformer 论文中提出，它允许有效地权衡更好的内存消耗与增加的时间消耗。

Reformer 中的分块前馈层

在 Reformer 中，*LSH* 或*局部*自注意力层通常后接残差连接，这便定义了*Transformer 块*的第一部分。有关此内容的更多详细信息，请参阅此博客。

*Transformer 块*第一部分的输出，称为*规范化自注意力*输出，可以写为 $\mathbf{\overline{Z}} = \mathbf{Z} + \mathbf{X}$，其中 $\mathbf{Z}$ 要么是 Reformer 中的 $\mathbf{Z}^{\text{LSH}}$，要么是 $\mathbf{Z}^\text{loc}$。

对于我们的示例输入 $\mathbf{x}_1, \ldots, \mathbf{x}_{16}$，我们如下所示地说明规范化自注意力输出。

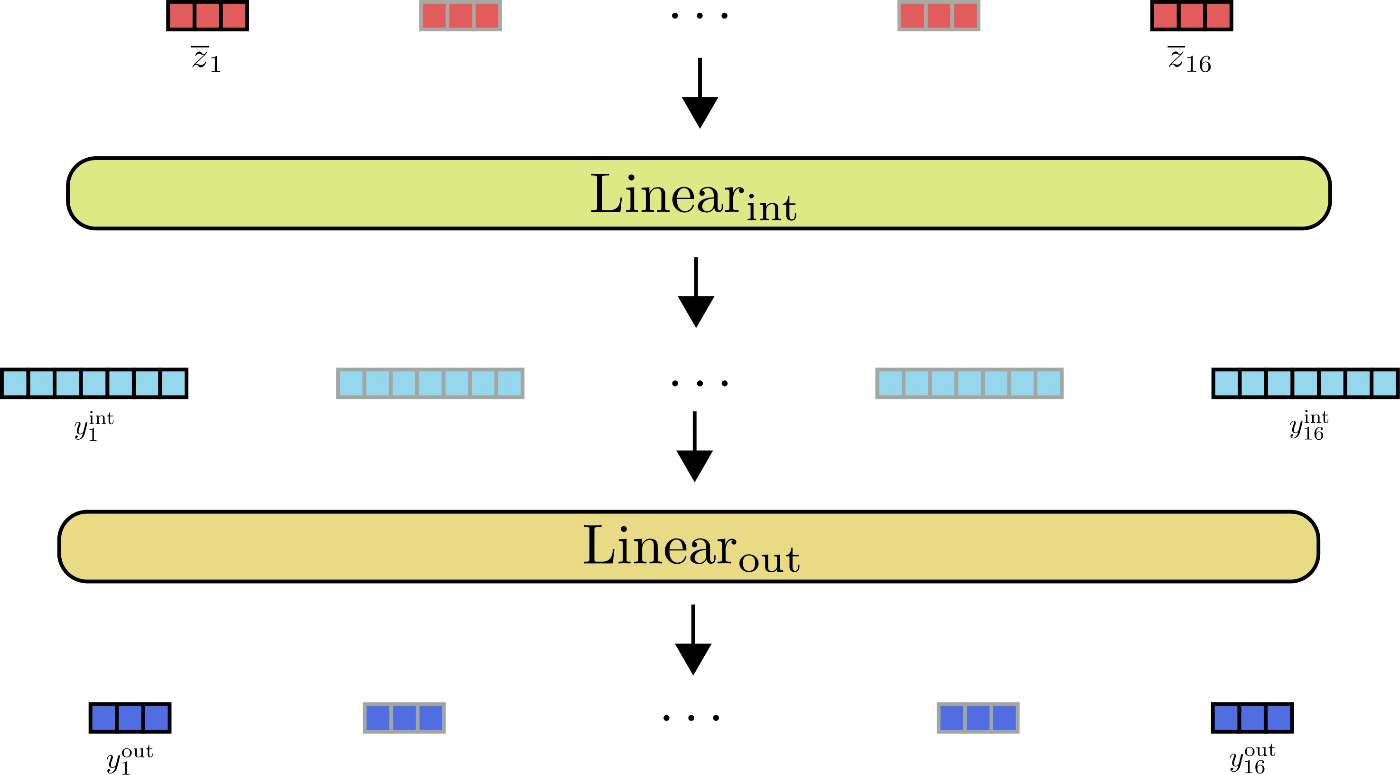
现在，*Transformer 块*的第二部分通常由两个前馈层 $^{1}$ 组成，定义为 $\text{Linear}_{\text{int}}(\ldots)$，用于处理 $\mathbf{\overline{Z}}$，得到中间输出 $\mathbf{Y}_{\text{int}}$ 和 $\text{Linear}_{\text{out}}(\ldots)$，用于处理中间输出，得到输出 $\mathbf{Y}_{\text{out}}$。这两个前馈层可以定义为

$$\mathbf{Y}_{\text{out}} = \text{Linear}_{\text{out}}(\mathbf{Y}_\text{int}) = \text{Linear}_{\text{out}}(\text{Linear}_{\text{int}}(\mathbf{\overline{Z}})).$$

此时重要的是要记住，从数学上讲，前馈层在位置 $\mathbf{y}_{\text{out}, i}$ 的输出仅取决于此位置的输入 $\mathbf{\overline{y}}_{i}$。与自注意力层不同，每个输出 $\mathbf{y}_{\text{out}, i}$ 完全独立于不同位置的所有输入 $\mathbf{\overline{y}}_{j \ne i}$。

让我们为 $\mathbf{\overline{z}}_1, \ldots, \mathbf{\overline{z}}_{16}$ 说明前馈层。

从图中可以看出，所有输入向量 $\mathbf{\overline{z}}_{i}$ 都由相同的前馈层并行处理。

当我们查看前馈层的输出维度时，会变得有趣。在 Reformer 中，$\text{Linear}_{\text{int}}$ 的输出维度定义为 config.feed_forward_size，例如 $d_{f}$，而 $\text{Linear}_{\text{out}}$ 的输出维度定义为 config.hidden_size，即 $d_{h}$。

Reformer 的作者观察到，在 Transformer 模型中，中间维度 $d_{f}$ 通常远大于输出维度 $^{2}$ $d_{h}$。这意味着维度为 $d_{f} \times n$ 的张量 $\mathbf{\mathbf{Y}}_\text{int}$ 分配了总内存的很大一部分，甚至可能成为内存瓶颈。

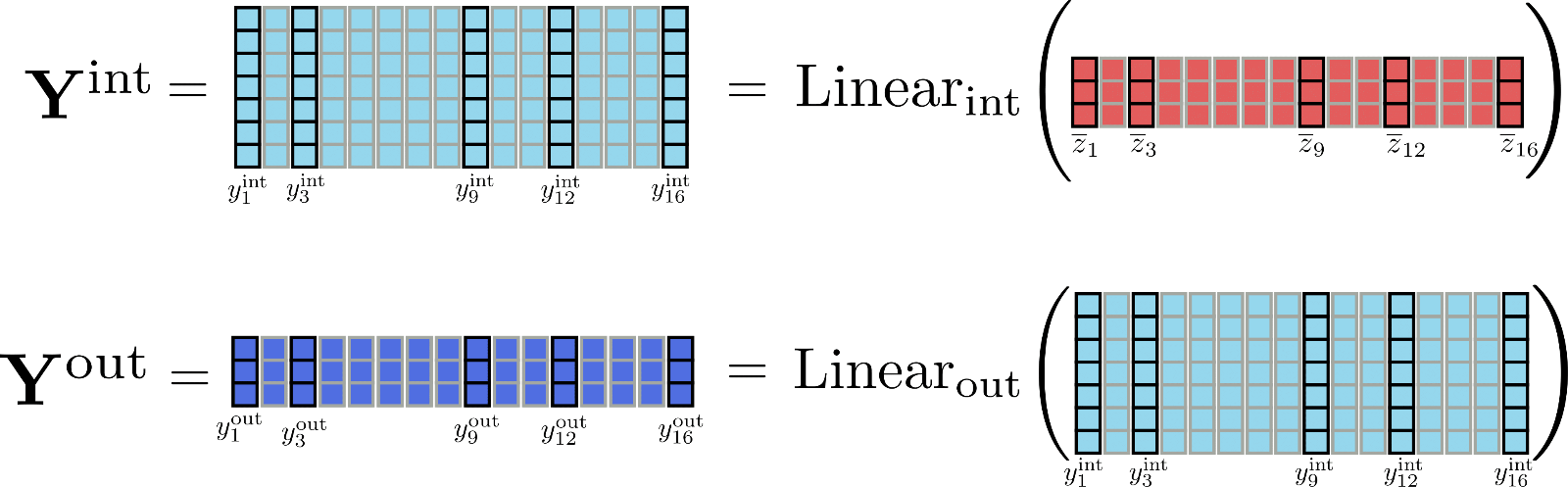
为了更好地理解维度差异，我们以示例为例，描绘矩阵 $\mathbf{Y}_\text{int}$ 和 $\mathbf{Y}_\text{out}$。

很明显，张量 $\mathbf{Y}_\text{int}$ 占用内存要大得多（确切地说，是 $\frac{d_{f}}{d_{h}} \times n$ 倍）比 $\mathbf{Y}_{\text{out}}$ 大。但是，是否真的有必要计算完整的中间矩阵 $\mathbf{Y}_\text{int}$ 呢？并非如此，因为相关的只有输出矩阵 $\mathbf{Y}_\text{out}$。因此，为了用内存换取速度，可以将线性层的计算分块，一次只处理一个块。将 config.chunk_size_feed_forward 定义为 $c_{f}$，分块线性层定义为 $\mathbf{Y}_{\text{out}} = \left[\mathbf{Y}_{\text{out}, 1: c_{f}}, \ldots, \mathbf{Y}_{\text{out}, (n - c_{f}): n}\right]$，其中 $\mathbf{Y}_{\text{out}, (c_{f} * i): (i * c_{f} + i)} = \text{Linear}_{\text{out}}(\text{Linear}_{\text{int}}(\mathbf{\overline{Z}}_{(c_{f} * i): (i * c_{f} + i)}))$。实际上，这仅意味着输出是逐步计算并连接起来的，以避免在内存中存储整个中间张量 $\mathbf{Y}_{\text{int}}$。

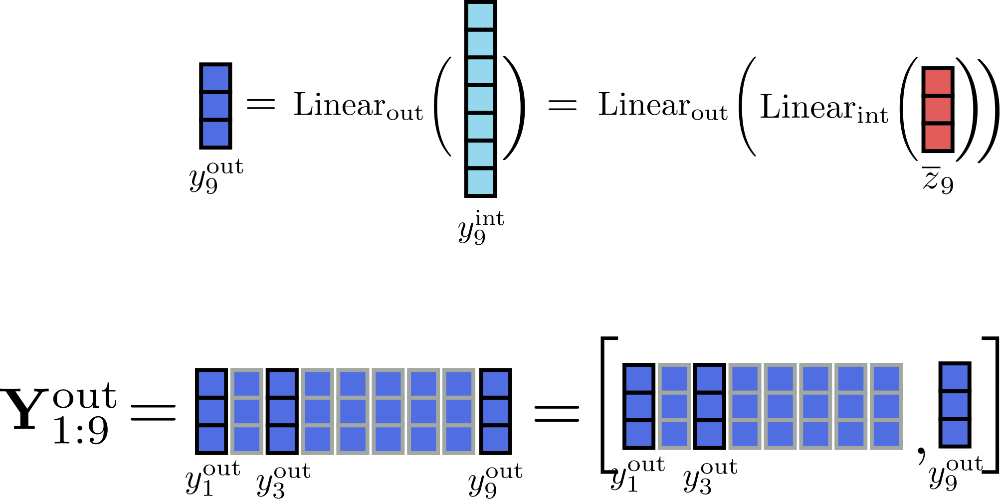
假设我们的示例中 $c_{f}=1$，我们可以如下所示说明位置 $i=9$ 的输出的增量计算。

通过以大小为 1 的块处理输入，唯一需要同时存储在内存中的张量是最大大小为 $16 \times d_{h}$ 的 $\mathbf{Y}_\text{out}$，大小为 $d_{f}$ 的 $\mathbf{y}_{\text{int}, i}$ 和大小为 $16 \times d_{h}$ 的输入 $\mathbf{\overline{Z}}$，其中 $d_{h}$ 是 config.hidden_size $^{3}$。

最后，重要的是要记住，**分块线性层**产生的输出在数学上等同于传统的线性层，因此可以应用于所有 Transformer 线性层。因此，利用 config.chunk_size_feed_forward 可以在某些使用场景下实现内存和速度之间更好的权衡。

${}^1$ 为了更简单的解释，通常在被前馈层处理之前应用于 $\mathbf{\overline{Z}}$ 的层归一化层暂时省略。

${}^2$ 例如，在 bert-base-uncased 中，中间维度 $d_{f}$ 为 3072，是输出维度 $d_{h}$ 的四倍。

${}^3$ 提醒一下，为了清晰和说明，本笔记本中假设输出 config.num_attention_heads 为 1，因此自注意力层的输出可以假定为 config.hidden_size 大小。

有关分块线性/前馈层的更多信息，也可以在 🤗Transformers 文档的此处找到。

基准测试

#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml

from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments

  Building wheel for transformers (setup.py) ... [?25l[?25hdone

config_no_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8")  # no chunk
config_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=1)  # feed forward chunk
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[1024, 2048, 4096], batch_sizes=[8], models=["Reformer-No-Chunk", "Reformer-Chunk"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_chunk, config_chunk], args=benchmark_args)
result = benchmark.run()

1 / 2
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 7.85 GiB already allocated; 1.74 GiB free; 9.06 GiB reserved in total by PyTorch)
2 / 2
Doesn't fit on GPU. CUDA out of memory. Tried to allocate 2.00 GiB (GPU 0; 11.17 GiB total capacity; 7.85 GiB already allocated; 1.24 GiB free; 9.56 GiB reserved in total by PyTorch)

====================      INFERENCE - MEMORY - RESULT       ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
      Reformer-No-Chunk              8              1024            4281     
      Reformer-No-Chunk              8              2048            7607     
      Reformer-No-Chunk              8              4096            N/A      
        Reformer-Chunk               8              1024            4309     
        Reformer-Chunk               8              2048            7669     
        Reformer-Chunk               8              4096            N/A      
--------------------------------------------------------------------------------

config_no_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=0, num_attention_{h}eads=2, feed_forward_size=16384)  # no chuck
config_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=1, num_attention_{h}eads=2, feed_forward_size=16384)  # feed forward chunk
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[1024, 2048, 4096], batch_sizes=[8], models=["Reformer-No-Chunk", "Reformer-Chunk"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_chunk, config_chunk], args=benchmark_args)
result = benchmark.run()

1 / 2
2 / 2

====================      INFERENCE - MEMORY - RESULT       ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
      Reformer-No-Chunk              8              1024            3743     
      Reformer-No-Chunk              8              2048            5539     
      Reformer-No-Chunk              8              4096            9087     
        Reformer-Chunk               8              1024            2973     
        Reformer-Chunk               8              2048            3999     
        Reformer-Chunk               8              4096            6011     
--------------------------------------------------------------------------------

3. 可逆残差层

可逆残差层最初由N. Gomez 等人提出，用于在训练流行的 *ResNet* 模型时减少内存消耗。在数学上，可逆残差层与“真正”的残差层略有不同，但不需要在正向传播期间保存激活，这可以显著减少训练期间的内存消耗。

Reformer 中的可逆残差层

让我们首先探讨为什么训练模型比模型推理需要更多的内存。

在模型推理时，所需的内存或多或少等于模型中**单个**最大张量所需的内存。另一方面，在训练模型时，所需的内存或多或少等于所有可微分张量的**总和**。

考虑到深度学习框架中自动微分的工作方式，这并不奇怪。多伦多大学 Roger Grosse 的这些讲座幻灯片对于更好地理解自动微分很有帮助。

简而言之，为了计算可微分函数（例如，一个层）的梯度，自动微分需要函数的输出梯度以及函数的输入和输出张量。虽然梯度是动态计算并随后丢弃的，但函数的输入和输出张量（也称为激活）在正向传播期间被存储。

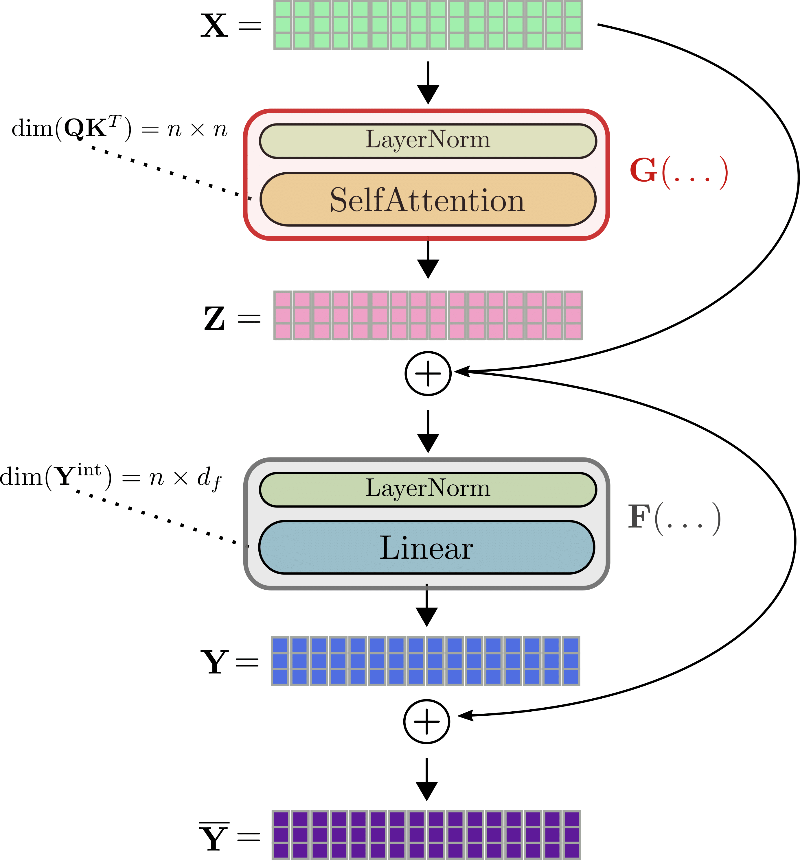
好的，让我们将其应用于 Transformer 模型。Transformer 模型包含多个所谓的 Transformer 层堆栈。每个额外的 Transformer 层都强制模型在正向传播期间存储更多的激活，从而增加训练所需的内存。让我们仔细看看。Transformer 层本质上由两个残差层组成。第一个残差层表示第 1 节中解释的 *自注意力* 机制，第二个残差层表示第 2 节中解释的 *线性* 或前馈层。

使用与之前相同的符号，Transformer 层的输入，即 $\mathbf{X}$，首先被归一化 $^{1}$，然后由自注意力层处理以获得输出 $\mathbf{Z} = \text{SelfAttn}(\text{LayerNorm}(\mathbf{X}))$。我们将这两个层缩写为 $G$，因此 $\mathbf{Z} = G(\mathbf{X})$。接下来，残差 $\mathbf{Z}$ 被添加到输入 $\mathbf{\overline{Z}} = \mathbf{Z} + \mathbf{X}$，并将总和输入到第二个残差层——两个线性层。$\mathbf{\overline{Z}}$ 由第二个归一化层处理，然后是两个线性层，得到 $\mathbf{Y} = \text{Linear}(\text{LayerNorm}(\mathbf{Z} + \mathbf{X}))$。我们将第二个归一化层和两个线性层缩写为 $F$，得到 $\mathbf{Y} = F(\mathbf{\overline{Z}})$。最后，残差 $\mathbf{Y}$ 被添加到 $\mathbf{\overline{Z}}$，从而得到 Transformer 层的输出 $\mathbf{\overline{Y}} = \mathbf{Y} + \mathbf{\overline{Z}}$。

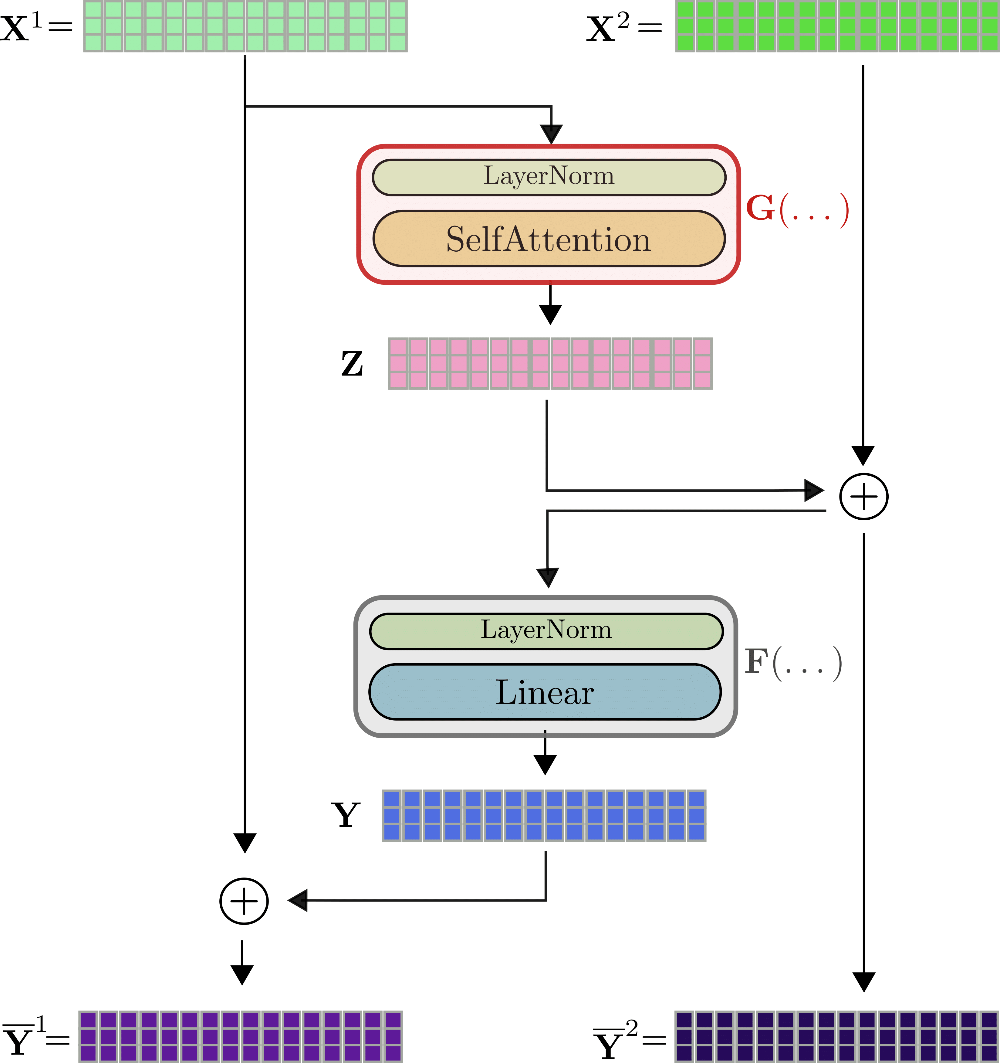
让我们以 $\mathbf{x}_1, \ldots, \mathbf{x}_{16}$ 为例，说明一个完整的 Transformer 层。

为了计算例如自注意力块 $G$ 的梯度，需要提前知道三个张量：梯度 $\partial \mathbf{Z}$、输出 $\mathbf{Z}$ 和输入 $\mathbf{X}$。虽然 $\partial \mathbf{Z}$ 可以即时计算并随后丢弃，但 $\mathbf{Z}$ 和 $\mathbf{X}$ 的值必须在正向传播期间计算和存储，因为在反向传播期间无法轻松即时重新计算它们。因此，在正向传播期间，大型张量输出，例如查询-键点积矩阵 $\mathbf{Q}\mathbf{K}^T$ 或线性层的中间输出 $\mathbf{Y}^{\text{int}}$，必须存储在内存中 $^{2}$。

在这里，可逆残差层就派上用场了。其思想相对简单。残差块的设计方式是，无需存储函数的输入和输出张量，而是在反向传播期间可以轻松地重新计算两者，这样在正向传播期间就无需在内存中存储任何张量。这是通过使用两个输入流 $\mathbf{X}^{(1)}, \mathbf{X}^{(2)}$ 和两个输出流 $\mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)}$ 实现的。第一个残差 $\mathbf{Z}$ 由第一个输出流计算，即 $\mathbf{Z} = G(\mathbf{X}^{(1)})$，并随后添加到第二个输入流的输入中，使得 $\mathbf{\overline{Z}} = \mathbf{Z} + \mathbf{X}^{(2)}$。同样，残差 $\mathbf{Y} = F(\mathbf{\overline{Z}})$ 再次添加到第一个输入流中，因此两个输出流定义为 $\mathbf{Y}^{(1)} = \mathbf{Y} + \mathbf{X}^{(1)}$ 和 $\mathbf{Y}^{(2)} = \mathbf{X}^{(2)} + \mathbf{Z} = \mathbf{\overline{Z}}$。

可逆Transformer层可进行可视化，例如$\mathbf{x}_1, \ldots, \mathbf{x}_{16}$，如下所示。

可以看出，输出$\mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)}$的计算方式与不可逆层中的$\mathbf{\overline{Y}}$非常相似，但它们在数学上是不同的。Reformer的作者在一些初步实验中观察到，可逆Transformer模型的性能与标准Transformer模型的性能相匹配。与标准Transformer层的第一个显著区别是，它有两个输入流和两个输出流$^{3}$，这最初会稍微增加前向传播所需的内存。然而，双流架构对于前向传播过程中无需保存任何激活是至关重要的。我们来解释一下。对于反向传播，可逆Transformer层需要计算梯度$\partial G$和$\partial F$。除了可以即时计算的梯度$\partial \mathbf{Y}$和$\partial \mathbf{Z}$之外，为了使自动微分生效，还需要知道$\partial F$的张量值$\mathbf{Y}$、$\mathbf{\overline{Z}}$，以及$\partial G$的张量值$\mathbf{Z}$和$\mathbf{X}^{(1)}$。

如果我们假设已知$\mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)}$，那么从图中很容易看出，可以如下计算$\mathbf{X}^{(1)}, \mathbf{X}^{(2)}$。$\mathbf{X}^{(1)} = F(\mathbf{\overline{Y}}^{(1)}) - \mathbf{\overline{Y}}^{(1)}$。很好，既然$\mathbf{X}^{(1)}$已知，$\mathbf{X}^{(2)}$可以通过$\mathbf{X}^{(2)} = \mathbf{\overline{Y}}^{(1)} - G(\mathbf{X}^{(1)})$计算。现在，$\mathbf{Z}$和$\mathbf{Y}$通过$\mathbf{Y} = \mathbf{\overline{Y}}^{(1)} - \mathbf{X}^{(1)}$和$\mathbf{Z} = \mathbf{\overline{Y}}^{(2)} - \mathbf{X}^{(2)}$可轻松计算。因此，结论是，如果在前向传播过程中仅存储**最后一个**可逆Transformer层的输出$\mathbf{\overline{Y}}^{(1)}, \mathbf{\overline{Y}}^{(2)}$，那么所有其他相关激活都可以通过在反向传播过程中利用$G$和$F$并传递$\mathbf{X}^{(1)}$和$\mathbf{X}^{(2)}$来推导。在反向传播过程中，每个可逆Transformer层G和F的两次前向传播开销，换取了前向传播过程中无需存储任何激活的优势。这是一个不错的权衡！

注：最近，主要的深度学习框架已经发布了代码，允许仅存储某些激活，并在反向传播期间重新计算较大的激活（Tensorflow 此处和PyTorch 此处）。对于标准可逆层，这仍然意味着每个Transformer层至少需要存储一个激活，但通过定义哪些激活可以动态重新计算，可以节省大量内存。

$^{1}$ 在前两节中，我们省略了自注意力层和线性层之前的层归一化层。读者应该知道，$\mathbf{X}$和$\mathbf{\overline{Z}}$在分别送入自注意力层和线性层之前，都经过了层归一化处理。$^{2}$ 尽管在设计中$\mathbf{Q}\mathbf{K}$的维度写为$n \times n$，但在*LSH自注意力*或*局部自注意力*层中，维度仅为$n \times l_{c} \times n_{h}$或$n \times l_{c}$，其中$l_{c}$是块长度，$n_{h}$是哈希数量。$^{3}$ 在第一个可逆Transformer层中，$\mathbf{X}^{(2)}$设置为等于$\mathbf{X}^{(1)}$。

基准测试

为了衡量可逆残差层的影响，我们将比较BERT与Reformer在训练过程中随着层数增加的内存消耗。

#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml

from transformers import ReformerConfig, BertConfig, PyTorchBenchmark, PyTorchBenchmarkArguments

让我们通过将层数从4增加到12来测量标准bert-base-uncased BERT模型所需的内存。

config_4_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=4)
config_8_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=8)
config_12_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=12)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Bert-4-Layers", "Bert-8-Layers", "Bert-12-Layers"], training=True, no_inference=True, no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_4_layers_bert, config_8_layers_bert, config_12_layers_bert], args=benchmark_args)
result = benchmark.run()

HBox(children=(FloatProgress(value=0.0, description='Downloading', max=433.0, style=ProgressStyle(description_…



1 / 3
2 / 3
3 / 3

====================        TRAIN - MEMORY - RESULTS        ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
        Bert-4-Layers                8              512             4103     
        Bert-8-Layers                8              512             5759     
        Bert-12-Layers               8              512             7415     
--------------------------------------------------------------------------------

可以看出，增加一层BERT会使所需内存线性增加超过400MB。

config_4_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=4, num_hashes=1)
config_8_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=8, num_hashes=1)
config_12_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=12, num_hashes=1)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Reformer-4-Layers", "Reformer-8-Layers", "Reformer-12-Layers"], training=True, no_inference=True, no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_4_layers_reformer, config_8_layers_reformer, config_12_layers_reformer], args=benchmark_args)
result = benchmark.run()

1 / 3
2 / 3
3 / 3

====================        TRAIN - MEMORY - RESULTS        ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
      Reformer-4-Layers              8              512             4607     
      Reformer-8-Layers              8              512             4987     
      Reformer-12-Layers             8              512             5367     
--------------------------------------------------------------------------------

另一方面，对于Reformer，在实践中，增加一层所需的内存会显著减少。增加一层平均会使所需内存增加不到100MB，因此一个更大的12层reformer-enwik8模型所需的内存比一个12层bert-base-uncased模型要少。

4. 轴向位置编码

Reformer使得处理巨大的输入序列成为可能。然而，对于如此长的输入序列，仅标准位置编码权重矩阵就会占用超过1GB的内存来存储其权重。为了防止如此大的位置编码矩阵，官方Reformer代码引入了*轴向位置编码*。

重要提示：*轴向位置编码未在官方论文中解释，但可以通过查看代码并与作者交流来很好地理解*

Reformer中的轴向位置编码

Transformer需要位置编码来解释输入中单词的顺序，因为自注意力层*没有顺序概念*。位置编码通常由一个简单的查找矩阵$\mathbf{E} = \left[\mathbf{e}_1, \ldots, \mathbf{e}_{n_\text{max}}\right]$定义。然后，位置编码向量$\mathbf{e}_{i}$简单地添加到第*i*个输入向量$\mathbf{x}_{i} + \mathbf{e}_{i}$上，这样模型就可以区分输入向量（也称为token）是在位置$i$还是$j$。对于每个输入位置，模型需要能够查找对应的位置编码向量，因此$\mathbf{E}$的维度由模型可以处理的最大输入向量长度config.max_position_embeddings（即$n_\text{max}$）和输入向量的config.hidden_size（即$d_{h}$）定义。

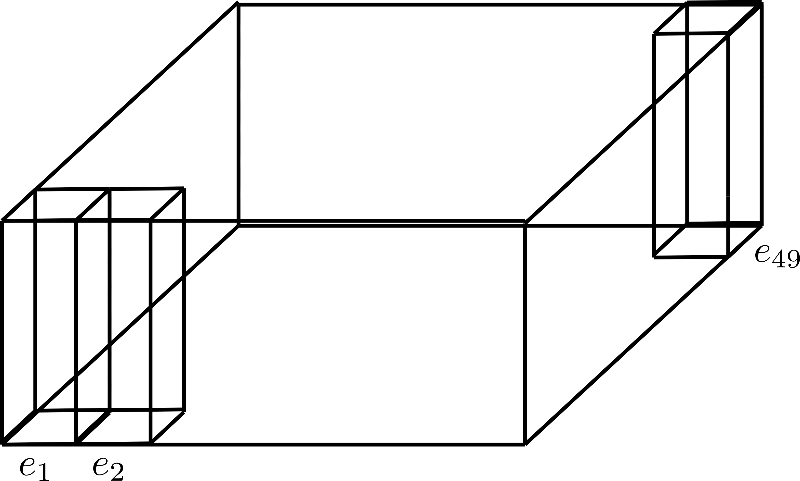
假设$d_{h}=4$且$n_\text{max}=49$，这样的位置编码矩阵可以如下可视化

这里，我们仅展示了维度（即高度）为4的位置编码$\mathbf{e}_{1}$、$\mathbf{e}_{2}$和$\mathbf{e}_{49}$。

假设我们希望训练一个Reformer模型，其序列长度可达0.5M个token，输入向量的`config.hidden_size`为1024（参见此处的notebook）。相应的位置嵌入大小为$0.5M \times 1024 \sim 512M$个参数，这相当于2GB的大小。

这样的位置编码在模型加载到内存和保存到硬盘时都会占用不必要的巨大内存量。

Reformer 的作者通过将 `config.hidden_size` 维度一分为二，并巧妙地将 $n_\text{max}$ 维度因子分解，从而大幅缩小了位置编码的尺寸。在 Transformer 中，用户可以通过将 `config.axial_pos_shape` 设置为两个适当的值 $n_\text{max}^1$ 和 $n_\text{max}^2$ 来决定 $n_\text{max}$ 可以分解成的形状，从而满足 $n_\text{max}^1 \times n_\text{max}^2 = n_\text{max}$。通过将 `config.axial_pos_embds_dim` 设置为两个适当的值 $d_{h}^{1}$ 和 $d_{h}^2$，从而满足 $d_{h}^1 + d_{h}^2 = d_{h}$，用户可以决定隐藏维度如何被切割。现在，让我们更直观地进行可视化和解释。

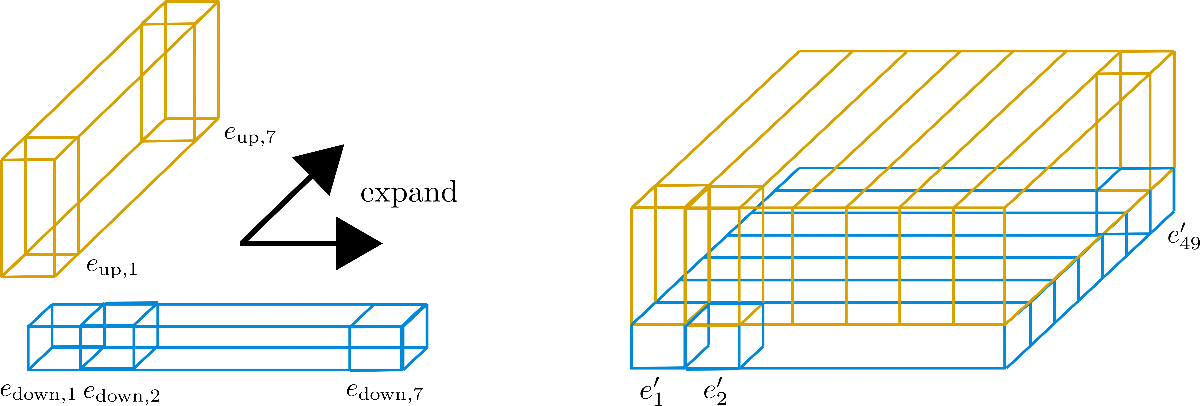
可以将$n_{\text{max}}$的因子分解想象成将维度折叠成第三个轴，这在以下`config.axial_pos_shape = [7, 7]`的因子分解中显示出来

三个竖立的矩形棱柱中的每一个都对应于编码向量 $\mathbf{e}_{1}, \mathbf{e}_{2}, \mathbf{e}_{49}$，但我们可以看到这49个编码向量被分成7行，每行7个向量。现在的想法是只使用7个编码向量中的一行，并将这些向量扩展到其他6行，本质上是重用它们的值。由于不鼓励不同编码向量具有相同的值，因此每个维度（又称高度）为config.hidden_size=4的向量被切割成大小为 $1$ 的下编码向量 $\mathbf{e}_\text{down}$ 和大小为 $3$ 的上编码向量 $\mathbf{e}_\text{up}$，这样下部分可以沿行维度扩展，上部分可以沿列维度扩展。让我们通过可视化来更清楚地了解。

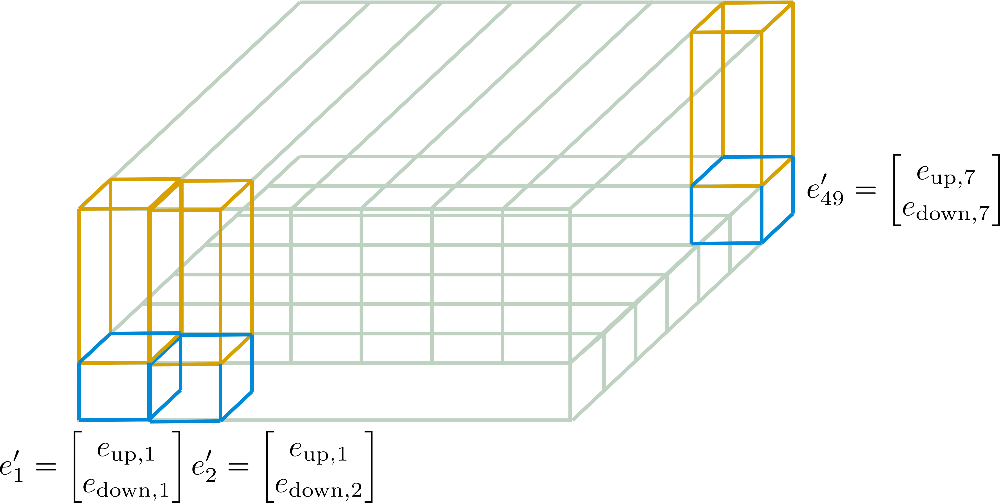
我们可以看到，我们将嵌入向量切割成 $\mathbf{e}_\text{down}$（蓝色部分）和 $\mathbf{e}_\text{up}$（黄色部分）。现在，对于“子”向量 $\mathbf{E}_\text{down} = \left[\mathbf{e}_{\text{down},1}, \ldots, \mathbf{e}_{\text{down},49}\right]$，只保留了第一行（即图中的宽度）的 $7$ 个向量，并沿列维度（即图的深度）进行扩展。反之，对于“子”向量 $\mathbf{E}_\text{up} = \left[\mathbf{e}_{\text{up},1}, \ldots, \mathbf{e}_{\text{up},49}\right]$，只保留了第一列的 $7$ 个向量，并沿行维度进行扩展。结果得到的嵌入向量 $\mathbf{e'}_{i}$ 则对应于

$$\mathbf{e'}_{i} = \left[ \left[\mathbf{e}_{\text{down, } i \% n_\text{max}^1}\right]^T, \left[\mathbf{e}_{\text{up, } \left \lfloor{\frac{i}{{n}^2_{\text{max}}}}\right \rfloor} \right]^T \right]^T$$

其中在我们的例子中 $n_\text{max}^1 = 7$ 和 $n_\text{max}^2 = 7$。这些新的编码 $\mathbf{E'} = \left[\mathbf{e'}_{1}, \ldots, \mathbf{e'}_{n_\text{max}}\right]$ 被称为 **轴向位置编码**。

下面将更详细地说明我们示例中的这些轴向位置编码。

现在应该更容易理解最终位置编码向量 $\mathbf{E'}$ 是如何仅从维度为 $d_{h}^1 \times n_{\text{max}^1}$ 的 $\mathbf{E}_{\text{down}}$ 和维度为 $d_{h}^2 \times n_{\text{max}}^2$ 的 $\mathbf{E}_{\text{up}}$ 计算得出的。

这里需要注意的关键一点是，轴向位置编码确保向量 $\left[\mathbf{e'}_1, \ldots, \mathbf{e'}_{n_{\text{max}}}\right]$ 在设计上彼此相等，并且编码矩阵的总体大小从 $n_{\text{max}} \times d_{h}$ 减少到 $n_{\text{max}}^1 \times d_{h}^1 + n_\text{max}^2 \times d_{h}^2$。通过让每个轴向位置编码向量在设计上不同，模型在学习高效位置表示方面获得了更大的灵活性，如果轴向位置编码由模型学习的话。

为了展示大小的显著减小，我们假设对于一个可以处理高达50万个token长度输入的Reform模型，我们将config.axial_pos_shape = [1024, 512]和config.axial_pos_embds_dim = [512, 512]。结果得到的轴向位置编码矩阵的大小将仅为 $1024 \times 512 + 512 \times 512 \sim 800K$ 个参数，大约相当于3MB。与此案例中标准位置编码矩阵所需的2GB相比，这是一个巨大的减少。

有关更简洁和数学密集的解释，请参阅 🤗Transformers 文档 此处。

基准测试

最后，我们还将比较传统位置嵌入和轴向位置嵌入的峰值内存消耗。

#@title Installs and Imports
# pip installs
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml

from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments, ReformerModel

位置嵌入仅依赖于两个配置参数：输入序列的最大允许长度 config.max_position_embeddings 和 config.hidden_size。让我们使用一个将输入序列最大允许长度推至五十万个token的模型，名为 google/reformer-crime-and-punishment，以查看使用轴向位置嵌入的效果。

首先，我们将比较轴向位置编码的形状与标准位置编码以及模型中的参数数量。

config_no_pos_axial_embeds = ReformerConfig.from_pretrained("google/reformer-crime-and-punishment", axial_pos_embds=False)  # disable axial positional embeddings
config_pos_axial_embeds = ReformerConfig.from_pretrained("google/reformer-crime-and-punishment", axial_pos_embds=True, axial_pos_embds_dim=(64, 192), axial_pos_shape=(512, 1024))  # enable axial positional embeddings

print("Default Positional Encodings")
print(20 * '-')
model = ReformerModel(config_no_pos_axial_embeds)
print(f"Positional embeddings shape: {model.embeddings.position_embeddings}")
print(f"Num parameters of model: {model.num_parameters()}")
print(20 * '-' + '\n\n')

print("Axial Positional Encodings")
print(20 * '-')
model = ReformerModel(config_pos_axial_embeds)
print(f"Positional embeddings shape: {model.embeddings.position_embeddings}")
print(f"Num parameters of model: {model.num_parameters()}")
print(20 * '-' + '\n\n')

HBox(children=(FloatProgress(value=0.0, description='Downloading', max=1151.0, style=ProgressStyle(description…



Default Positional Encodings
--------------------
Positional embeddings shape: PositionEmbeddings(
  (embedding): Embedding(524288, 256)
)
Num parameters of model: 136572416
--------------------


Axial Positional Encodings
--------------------
Positional embeddings shape: AxialPositionEmbeddings(
  (weights): ParameterList(
      (0): Parameter containing: [torch.FloatTensor of size 512x1x64]
      (1): Parameter containing: [torch.FloatTensor of size 1x1024x192]
  )
)
Num parameters of model: 2584064
--------------------

阅读了理论后，轴向位置编码权重的形状对于读者来说应该不足为奇。

关于结果，可以看出，对于能够处理如此长输入序列的模型，使用默认位置编码是不切实际的。在 `google/reformer-crime-and-punishment` 的情况下，仅标准位置编码就包含超过1亿个参数。轴向位置编码将此数字减少到仅20多万个。

最后，我们再来比较一下推理时的内存需求。

benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Reformer-No-Axial-Pos-Embeddings", "Reformer-Axial-Pos-Embeddings"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_pos_axial_embeds, config_pos_axial_embeds], args=benchmark_args)
result = benchmark.run()

1 / 2
2 / 2

====================      INFERENCE - MEMORY - RESULT       ====================
--------------------------------------------------------------------------------
          Model Name             Batch Size     Seq Length    Memory in MB 
--------------------------------------------------------------------------------
Reformer-No-Axial-Pos-Embeddin       8              512             959      
Reformer-Axial-Pos-Embeddings        8              512             447      
--------------------------------------------------------------------------------

可以看出，在使用 google/reformer-crime-and-punishment 的情况下，轴向位置嵌入将内存需求减少了大约一半。