推测解码的一种最优有损变体

社区文章发布于 2024 年 6 月 12 日

Alice and Bob using speculative decoding

推测解码 (Leviathan 等，2023；Chen 等，2023) 是一种用于自回归语言模型的优雅解码策略。它在保持目标分布的同时加速文本生成。在本篇博文中，我将介绍导师解码，这是一种新颖的、可证明最优的、有损的推测解码变体。它以目标分布的有限偏差为代价，进一步提高了解码速度。

我将首先总结推测解码的原理。然后，我将介绍导师解码并解释其最优性。最后，我将评论一些初步的实验结果并提出进一步的探索。

推测解码

让我先讲一个故事，希望能帮助您理解推测解码，以及在接下来的章节中理解导师解码。爱丽丝是一位才华横溢的作家，但她说话或写作非常慢。幸运的是，她的长期助手鲍勃一直以以下方式帮助她写作：

根据当前手稿和他对爱丽丝作品的了解，鲍勃想象接下来的几个词会是什么，并写下这些候选词；
爱丽丝指出她自己确实可以写出来的最后一个候选词；
爱丽丝写下下一个词；
在步骤 2 和 3 中选择的所有词都被添加到手稿中，其他候选词被丢弃，然后我们回到步骤 1。

如果鲍勃能很好地猜出爱丽丝的下一个词，并且写得比她快得多，这可以节省大量时间。此外，最终的手稿将与爱丽丝独自写出的书 indistinguishable。

现在您可能已经清楚，爱丽丝和鲍勃实际上对应于自回归语言模型。与块式并行解码 (Stern 等，2018) 或辅助生成 (Joao Gante，2023) 类似，推测解码结合了一个大型的目标模型和一个小型草稿模型（通常比目标模型小十倍）。

更准确地说，假设

分词器的词汇表是 $V$ ；
草稿模型的下一个 token 概率分布是 $p (. ∣ .)$ ；
目标模型的下一个 token 概率分布是 $q (. ∣ .)$ ；
初始提示和目前已生成的文本是 $x_{1}, . . ., x_{n}$ ；

……推测解码将按以下方式选择下一个 token：

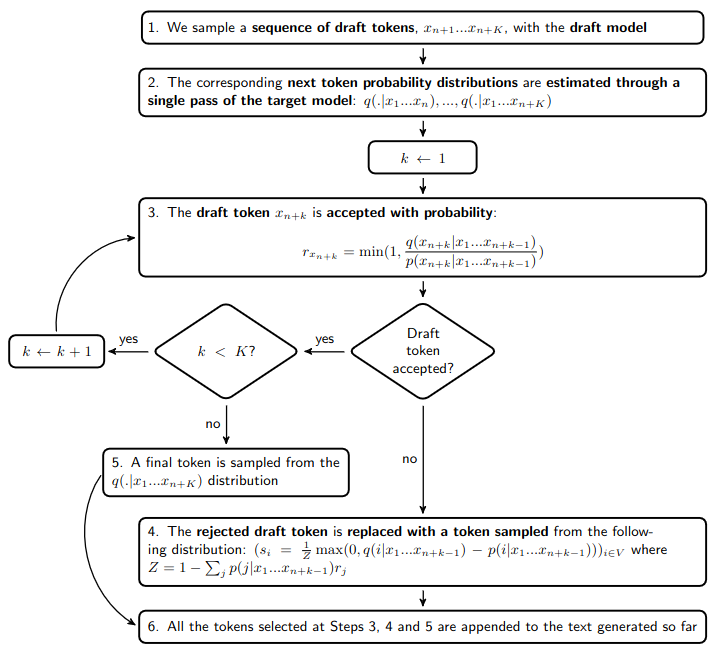
推测解码通常将解码速度提高一倍。这种加速来自于这样一个事实：在步骤 2 中，用目标模型估计下一个 token 的概率分布所需的时间大约与用该目标模型生成一个 token 的时间相同。此外，步骤 3 中的接受概率 $r_{x_{n+k}}$ 和步骤 4 中的替换 token 概率分布 $(s_i)_{i \in V}$ 的公式使得生成的文本可证明地遵循目标分布。

在此条件下，这些公式实际上最大化了接受草稿 token 的概率： $\sum_{i \in V} p_i r_i$ 。这意味着如果我们想要进一步提高这个概率，我们需要偏离目标分布。但是，我们先回到爱丽丝和鲍勃的故事……

导师解码

爱丽丝在完成她的绝世之作后，决定不再写作。她现在专注于指导鲍勃，鲍勃也渴望成为一名作家。他们合作的方式保持不变，只有一个重大区别：爱丽丝现在以不同的方式评估鲍勃建议的候选词序列。过去，爱丽丝会丢弃任何她自己不会写出的词。她现在希望鲍勃找到自己的风格，只拒绝明显不合适的词。例如，她可以拒绝拼写错误、笨拙的措辞或情节漏洞。

与以前的情况相比，爱丽丝打断鲍勃的次数减少了，他们的手稿进展得更快。最终的书籍不会与爱丽丝的书籍风格相同，但由于她的指导，它将具有高质量。

以类似的方式，我们现在准备以受控方式偏离目标分布，以增加接受草稿 token 的概率。更具体地说，我们希望找到 $(r_i)_{i \in V}$ 或 $(s_i)_{i \in V}$ 的值，使其在保持结果分布与目标分布之间的 Kullback-Leibler 散度在一个常数 $D$ 之下时，最大程度地增加接受 $i$ 的概率。

由于我们只关注一个 token，我们可以简化我们的符号

$p_i = p(i\mid x_1...x_{n+k-1})$ ;
$q_{i} = q (i ∣ x_{1} ...x_{n + k - 1})q_i = q(i\mid x_1...x_{n+k-1})$ ;
当没有明确指定哑变量时，例如在 $(r_{i})_{i}$ 、 $\sum_i$ 和 $\forall i$ 中，它们对应于整个词汇表： $(r_i)_{i \in V}$ 、 $\sum_{i \in V}$ 和 $\forall i \in V$ 。

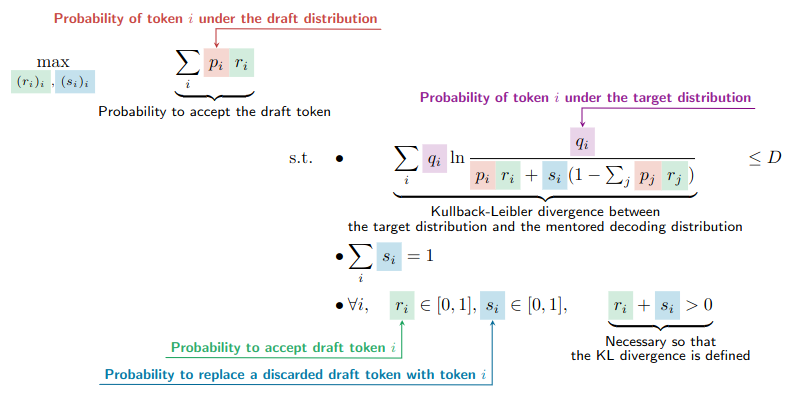
使用推测方法获得 token $i$ 的概率为 $\pi_i = p_ir_i + s_i (1 - \sum_j p_jr_j)$ (Chen 等，2023)，并且 $(r_{i})_{i}$ 或 $(s_{i})_{i}$ 是以下优化问题的解

解决优化问题

幸运的是，解决这个拥有接近 $10^{5}$ 个决策变量的非线性优化问题是可行的，且计算开销有限。在主要基于卡鲁什-库恩-塔克条件 (Kuhn & Tucker, 2013) 的附带证明中，我们表明：

在非平凡情况下存在唯一解；
对于此解， $(r_{i})_{i}$ $(r_{i})_{i}$ 或 $(s_{i})_{i}$ $(s_{i})_{i}$ 满足
- $r_i = \min(1, \frac{q_i}{\alpha p_i})$ 对于某个 $\alpha$
- $s_i = \frac{1}{1-\sum_jp_jr_j}\max(0, \frac{q_i}{\beta}-p_i)$ 对于某个 $\beta$
在非平凡情况下， $\alpha$ 和 $\beta$ 之间存在一对一关系，因此选择 $\alpha \in ]0, 1]$ 足以找到某个 $D$ 的优化问题的解；
目标函数和第一个不等式约束中的 Kullback-Leibler 散度是 $\alpha$ 的递减函数。

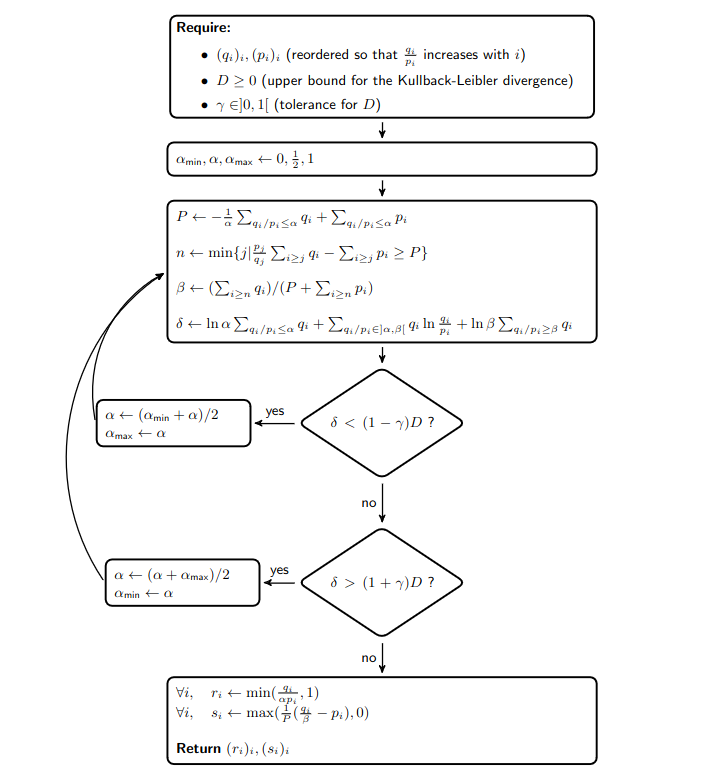
这些发现意味着使用二分查找 $\alpha$ 来计算优化问题的解是直截了当的。更具体地说，下图展示了导师解码算法

此外，以下事实减少了导师解码的计算开销

由于我们知道 $r_i \geq \min(1, \frac{q_i}{p_i})$ ，我们只有在接受或拒绝草稿 token 的随机抽样值 $u \sim U([0, 1])$ 大于 $\min(1, \frac{q_i}{p_i})$ 时，才需要计算 $r_{i}$ 和 $(s_{j})_{j}$ ；
当给定 token 的目标分布 $(q_{i})_{i}$ 和草稿分布 $(p_{i})_{i}$ 之间的 Kullback-Leibler 散度小于 $D$ 时，我们可以直接接受草稿 token；
在循环之前，可以以向量化方式计算 $(\sum_{i \leq j} q_i)_j$ 、 $(\sum_{i \leq j} p_i)_j$ 、 $(\sum_{i \geq j} q_i)_j$ 、 $(\sum_{i \geq j} p_i)_j$ 、 $(\sum_{i \leq j} q_i \ln\frac{q_i}{p_i})_j$ 和 $(\frac{p_j}{q_j} \sum_{i \geq j} q_i - \sum_{i \geq j} p_i)_j$ 的所有值，从而节省时间。

初步实验结果

作为首次实验（完整代码在此），我使用 WMT15 数据集的一个子集，以 T5-large 和 T5-small 作为目标模型和草稿模型，测试了指导解码在英语到法语翻译任务上的表现。

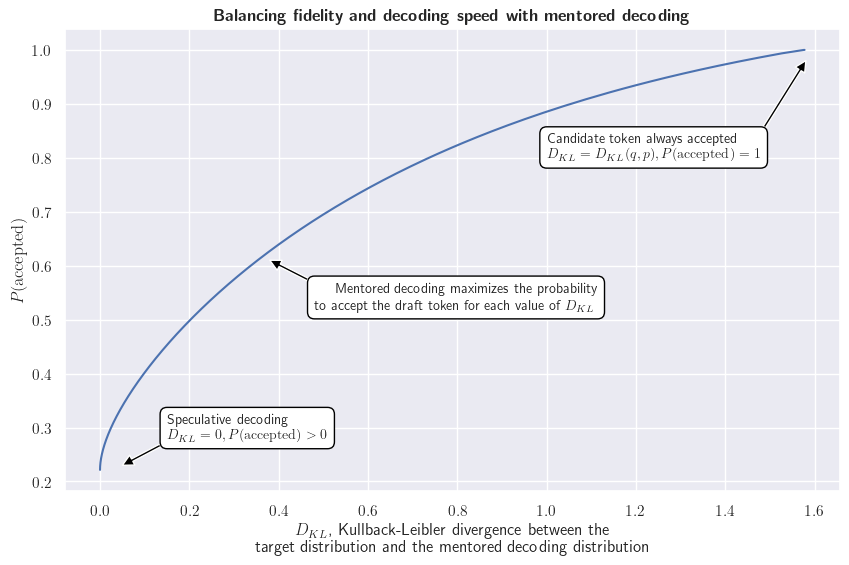
如果我们首先观察单个标记，我们可以可视化优化问题针对不同 Kullback-Leibler 散度值的解决方案。下表展示了接受草稿标记的概率 $\sum_i p_ir_i$ 和对目标分布的忠实度之间的平衡。

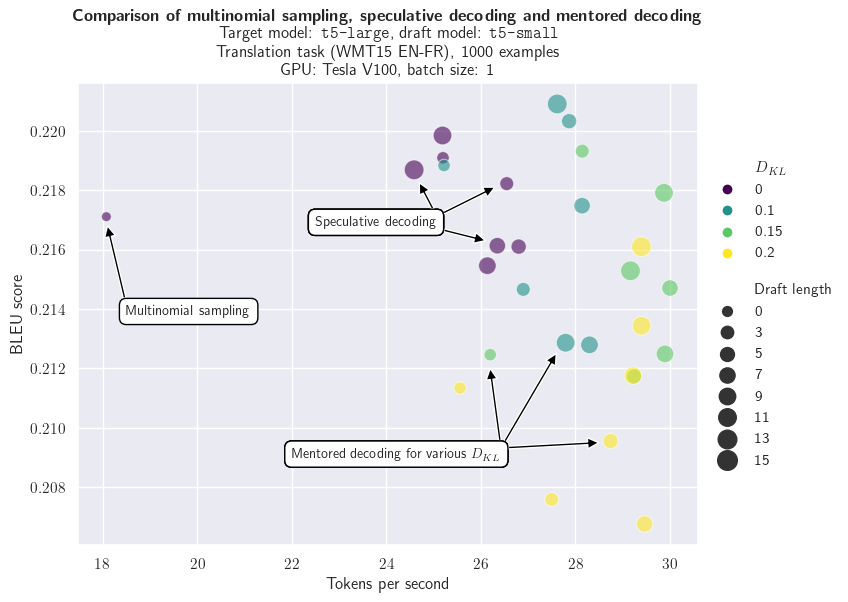
评估指导解码需要同时衡量解码速度和下游任务的性能指标，例如这里的 BLEU 分数。后者很重要：由于我们允许偏离目标分布，我们需要评估对目标任务的潜在影响。下图比较了多项式采样、推测解码和指导解码（仅限指导解码）在不同草稿长度和 Kullback-Leibler 散度值下的表现。我们可以看到：

与多项式采样相比，推测解码显著提高了解码速度；
指导解码进一步增加了每秒生成的标记数量;
与多项式采样相比，推测解码和 Kullback-Leibler 散度值最小的指导解码在 BLEU 分数上没有显著差异（这对于推测解码来说是预期的，因为目标分布得到了保留）；
不出所料，增加 Kullback-Leibler 散度既能加速文本生成，又会降低 BLEU 分数。

结论和未来工作

在本篇博客文章中，我介绍了一种推测解码的有损变体。它在给定目标分布和结果分布之间 Kullback-Leibler 散度边界的情况下，最大限度地提高接受草稿标记的概率。上述初步实验结果表明，指导解码可以提高解码速率，这种提升要么是适度的，对下游任务性能影响有限；要么是显著的，但会以性能明显下降为代价。

需要进行广泛的实验来探索指导解码所适用的任务和模型范围。特别地，以下直觉值得进行实证检验：

可以以各种方式编写有效答案的任务（例如翻译、摘要或思维链问答）将比有效答案范围狭窄的任务（例如语音转文本）更能受益于指导解码；
指导解码与高性能目标模型配合得更好，该模型不仅能够执行下游任务，而且能够评估其他措辞的有效答案。

非常感谢下文提及文章的作者以及为此工作所用各种软件库的维护者，特别是 Transformers、PyTorch、TikZ 和 annotate-equations。封面图片由 ArtOut 创建。

这篇博客文章最初发布在我的个人博客上。

社区

通过拖放到文本输入框、粘贴或点击此处上传图片、音频和视频。

点击或粘贴此处以上传图片

· 注册或登录发表评论