Q-Learning 入门 第 1 部分
Hugging Face 🤗 深度强化学习课程第二单元,第一部分
⚠️ 本文的**新更新版本可在此处获取** 👉 https://huggingface.co/deep-rl-course/unit1/introduction
本文是深度强化学习课程的一部分。这是一个从入门到精通的免费课程。请在此处查看课程大纲 here.

⚠️ 本文的**新更新版本可在此处获取** 👉 https://huggingface.co/deep-rl-course/unit1/introduction
本文是深度强化学习课程的一部分。这是一个从入门到精通的免费课程。请在此处查看课程大纲 here.
在本课程的第一章中,我们学习了强化学习 (RL)、RL 过程以及解决 RL 问题的不同方法。我们还训练了我们的第一个着陆器智能体,使其**成功降落在月球🌕上,并将其上传到 Hugging Face Hub。**
所以今天,我们将**深入探讨强化学习方法之一:基于价值的方法**,并学习我们的第一个 RL 算法:**Q-学习。**
我们还将**从头开始实现我们的第一个 RL 智能体**:一个 Q-学习智能体,并将在两个环境中训练它。
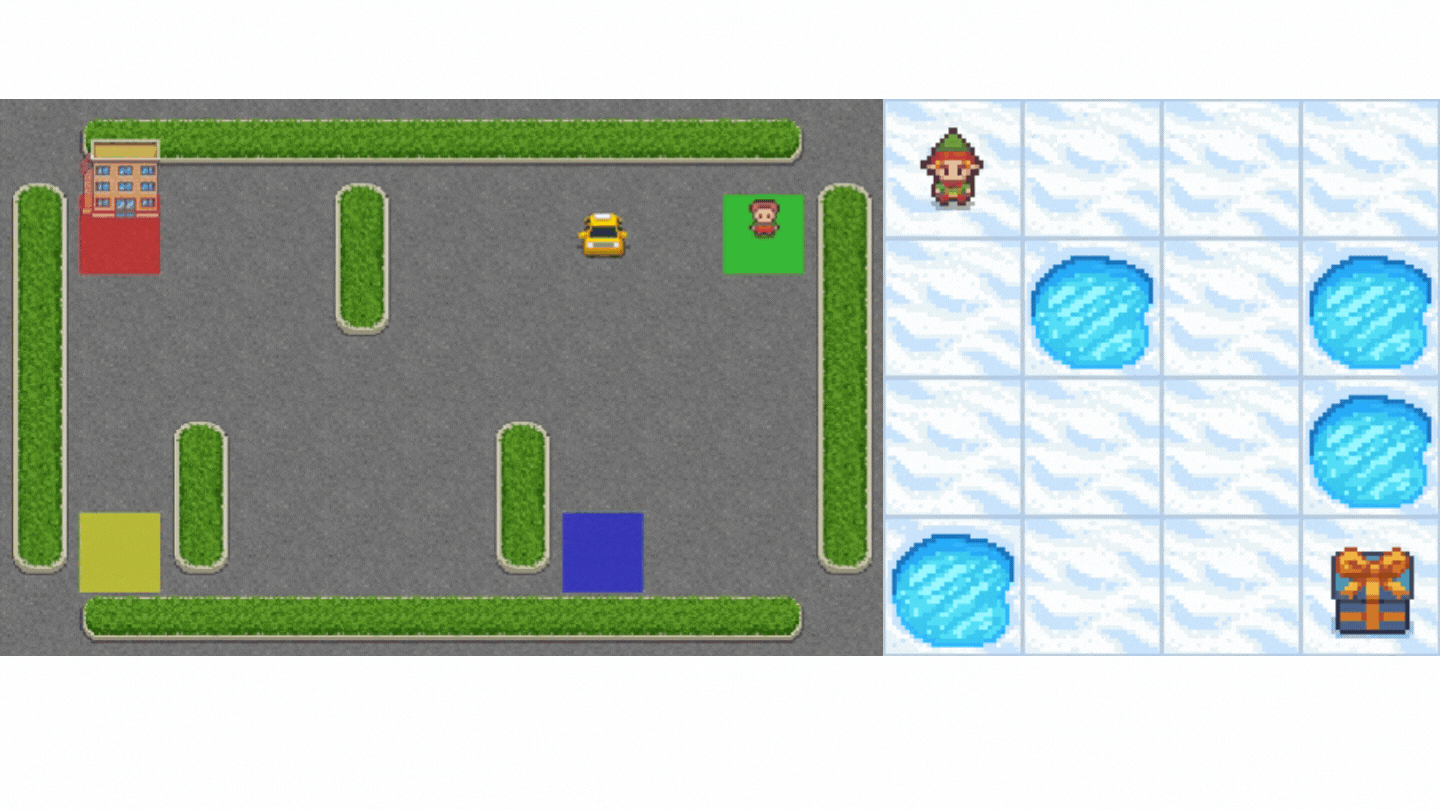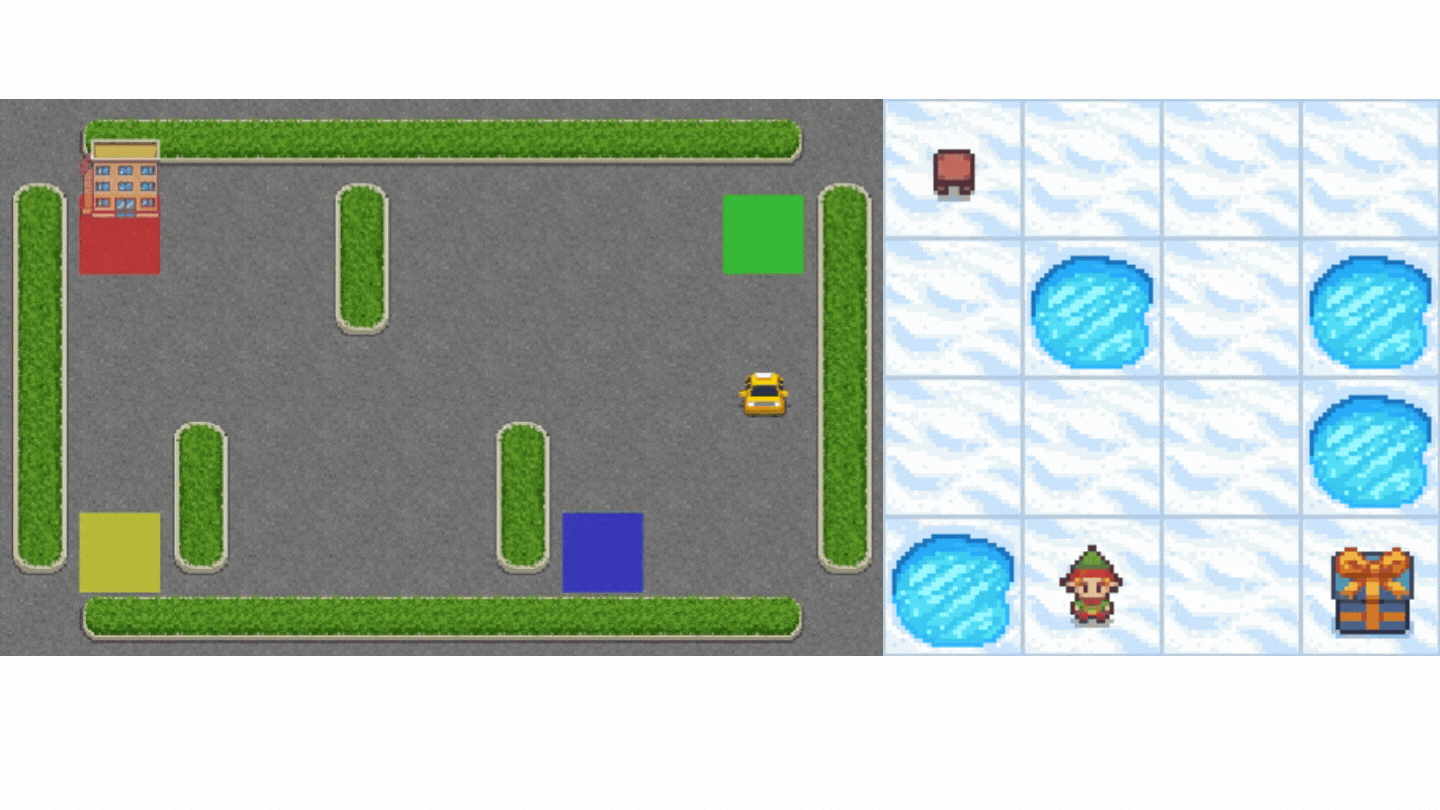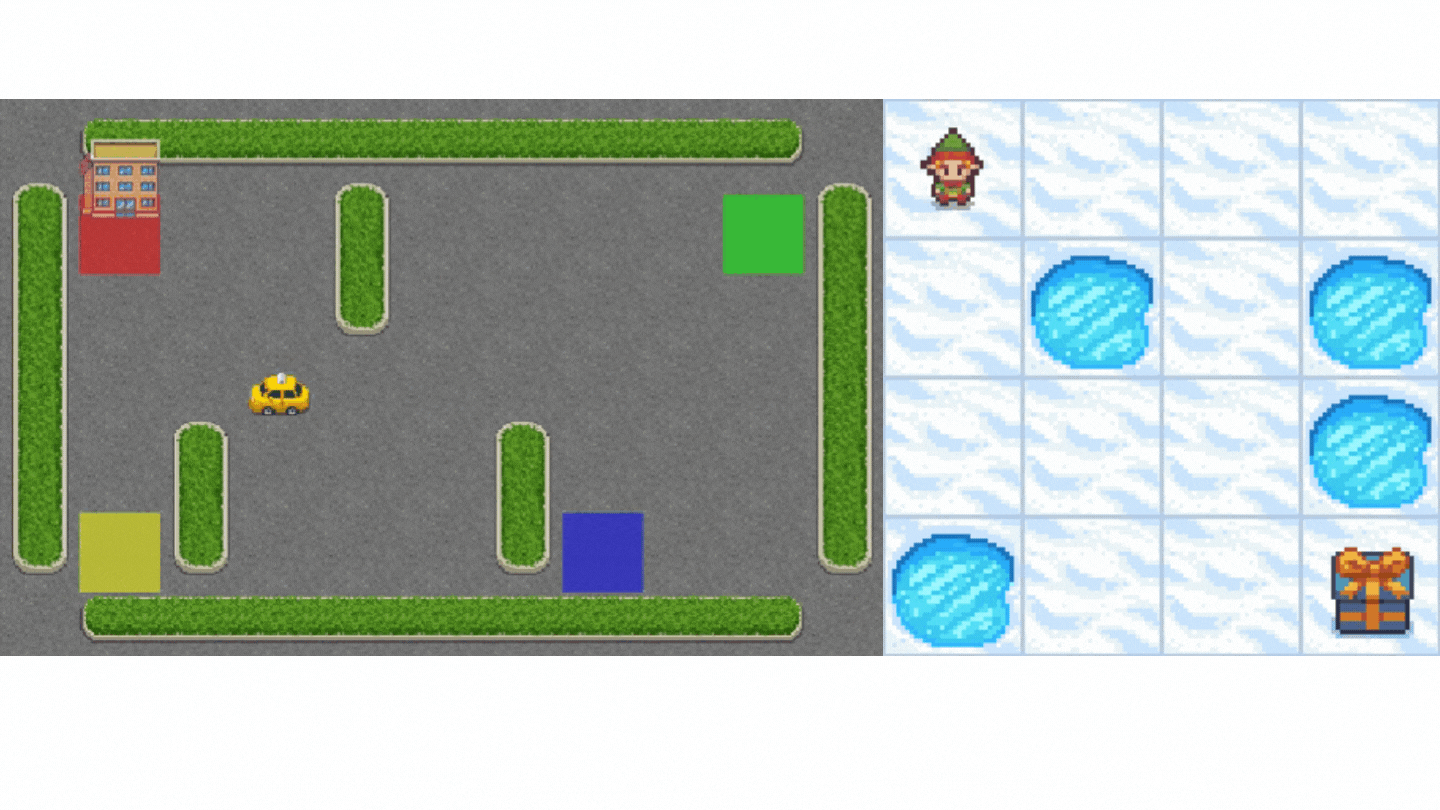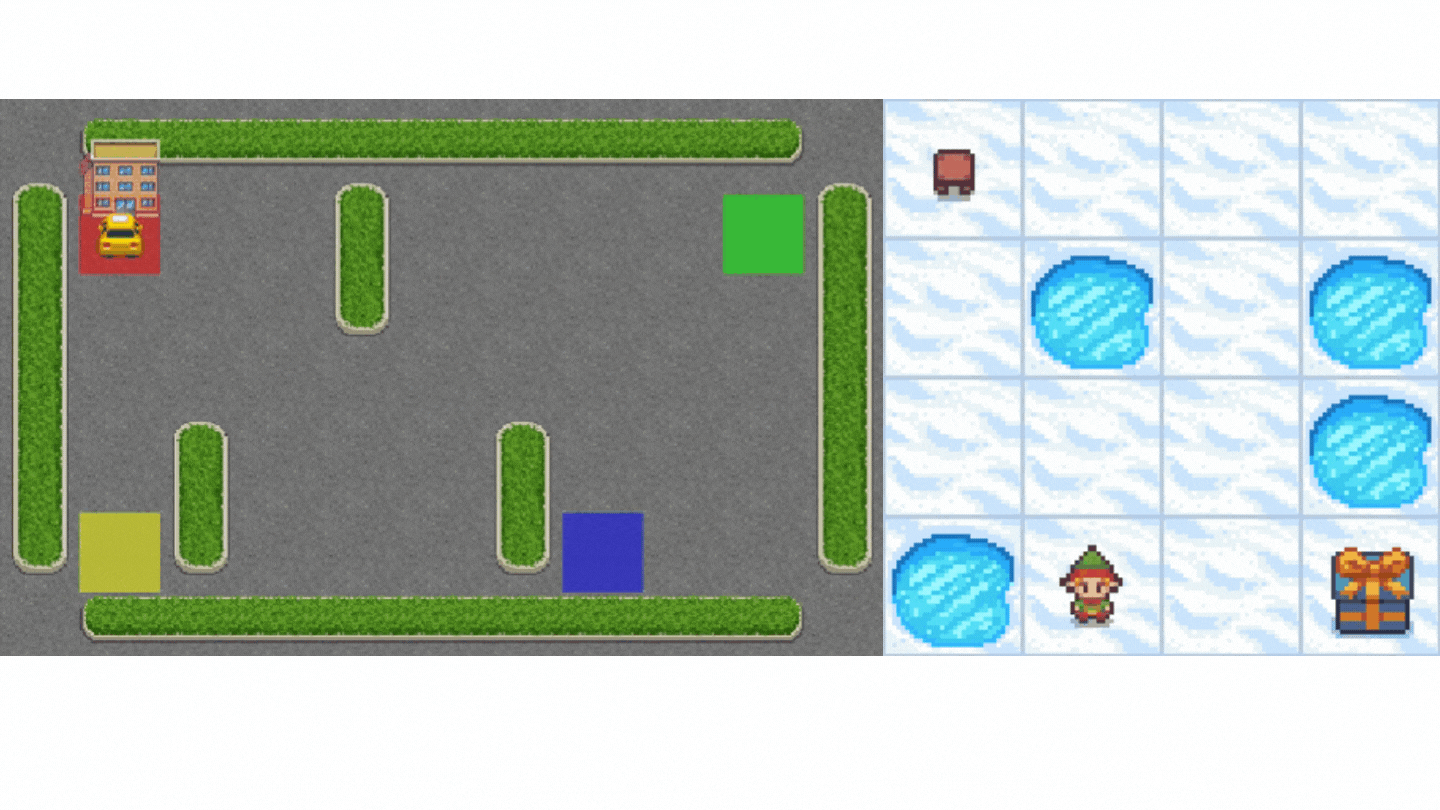
- Frozen-Lake-v1(非滑溜版本):我们的智能体需要**从起始状态 (S) 到目标状态 (G)**,只在冰冻的瓷砖 (F) 上行走并避开洞 (H)。
- 一辆自动驾驶出租车需要**学习导航**城市,以**将其乘客从 A 点运送到 B 点。**
本单元分为 2 部分。
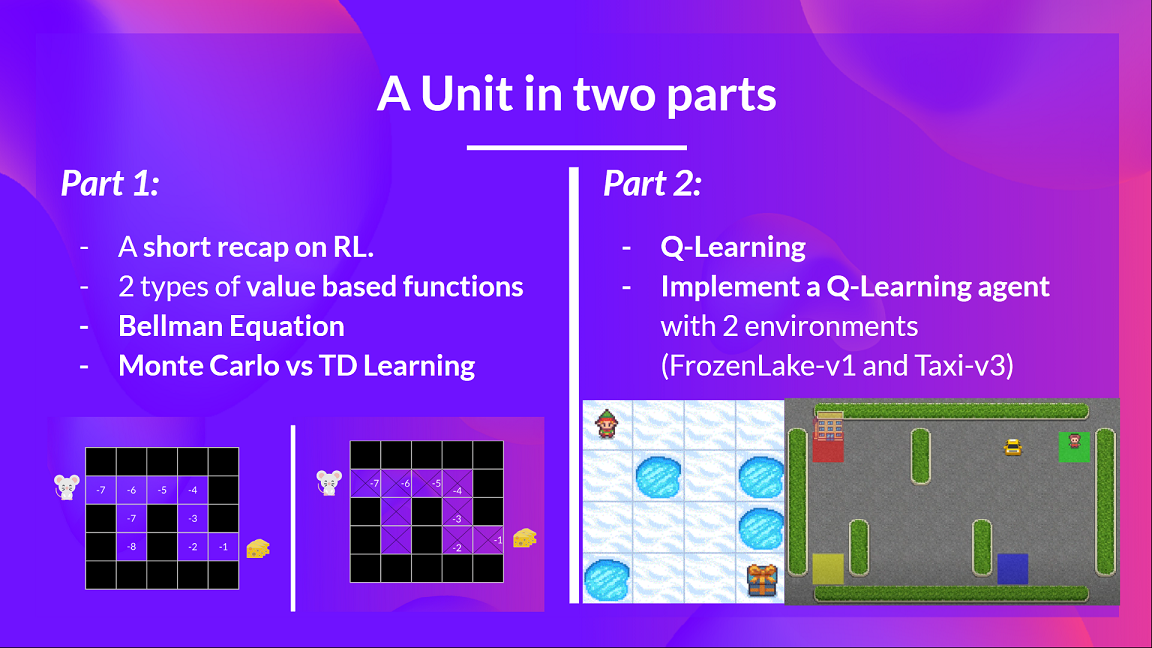
在第一部分中,我们将**学习基于价值的方法以及蒙特卡罗和时序差分学习之间的区别。**
在第二部分中,**我们将学习我们的第一个 RL 算法:Q-学习,并实现我们的第一个 RL 智能体。**
**如果你想深入研究深度 Q-学习**(第三单元),本单元至关重要:深度 Q-学习是第一个能够玩 Atari 游戏并在其中一些游戏(Breakout、Space Invaders 等)中**击败人类水平**的深度 RL 算法。
那么,让我们开始吧!
**什么是强化学习?简短回顾**
在强化学习中,我们构建一个可以**做出明智决策**的智能体。例如,一个**学习玩视频游戏**的智能体。或者一个交易智能体,通过**做出买卖股票的明智决策**来**最大化其收益**。
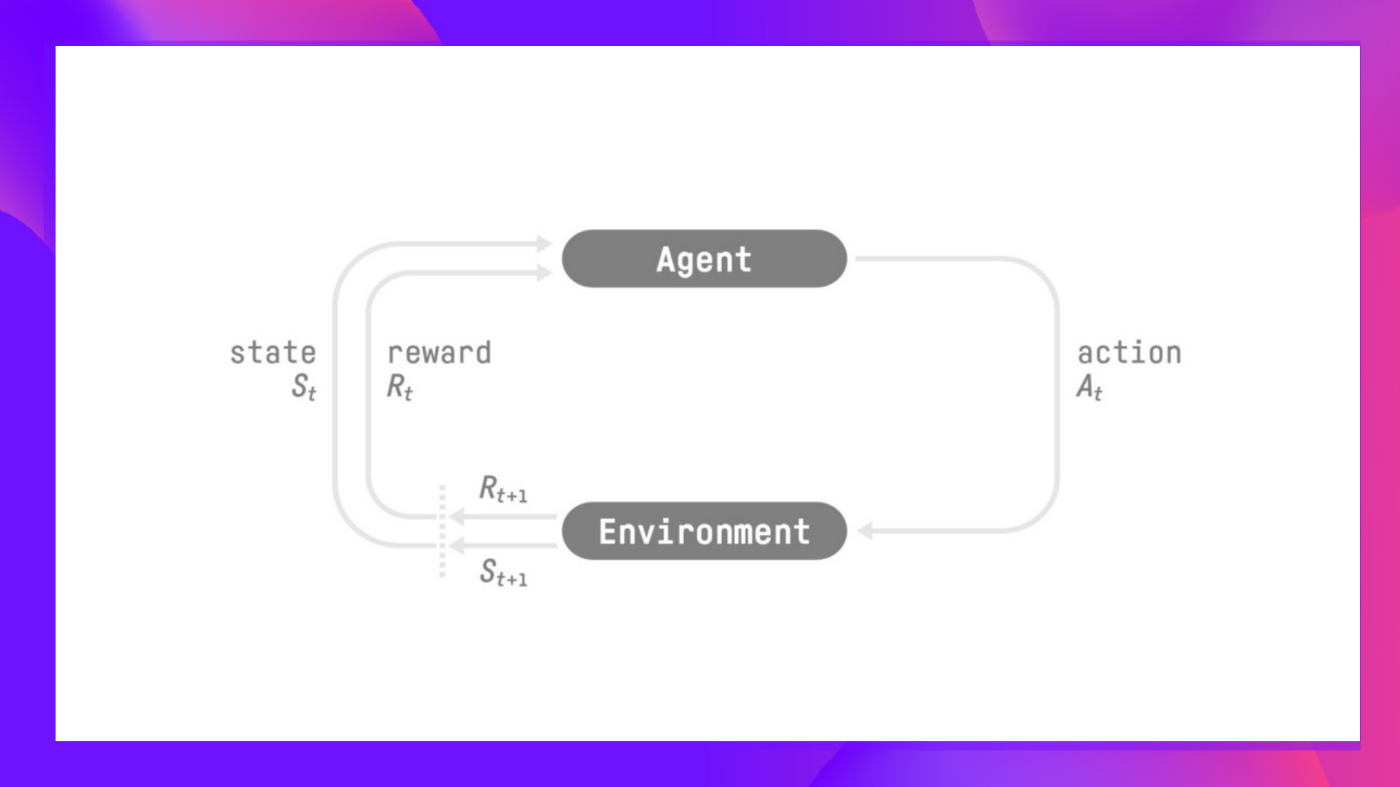
但是,为了做出智能决策,我们的智能体将通过**试错**与环境交互来学习,并获得(正面或负面)奖励作为**独特的反馈。**
其目标**是最大化其预期的累积奖励**(根据奖励假设)。
**智能体的决策过程称为策略 π:**给定一个状态,策略将输出一个动作或一个动作的概率分布。也就是说,给定环境的观察,策略将提供智能体应该采取的动作(或每个动作的多个概率)。

**我们的目标是找到一个最优策略 π** *,即,一个能够带来最佳预期累积奖励的策略。
为了找到这个最优策略(从而解决强化学习问题),**有两种主要的强化学习方法。**
- _基于策略的方法_:**直接训练策略**,以学习在给定状态下采取哪个动作。
- _基于价值的方法_:**训练一个价值函数**,以学习**哪个状态更有价值**,并使用这个价值函数**来采取导致该价值的动作。**

在本章中,**我们将深入探讨基于价值的方法。**
**两种基于价值的方法**
在基于价值的方法中,**我们学习一个价值函数**,它**将状态映射到在该状态下的预期价值。**

一个状态的价值是智能体**从该状态开始**并根据我们的策略行动后可以获得的**预期折扣回报**。
如果你忘记了什么是折扣,你可以阅读这一节。
但是,根据我们的策略行动是什么意思呢?毕竟,在基于价值的方法中我们没有策略,因为我们训练的是价值函数而不是策略。
请记住,**RL 智能体的目标是拥有一个最优策略 π。**
为了找到它,我们了解到有两种不同的方法。
- _基于策略的方法:_**直接训练策略**,以选择在给定状态下采取哪个动作(或在该状态下动作的概率分布)。在这种情况下,我们**没有价值函数。**
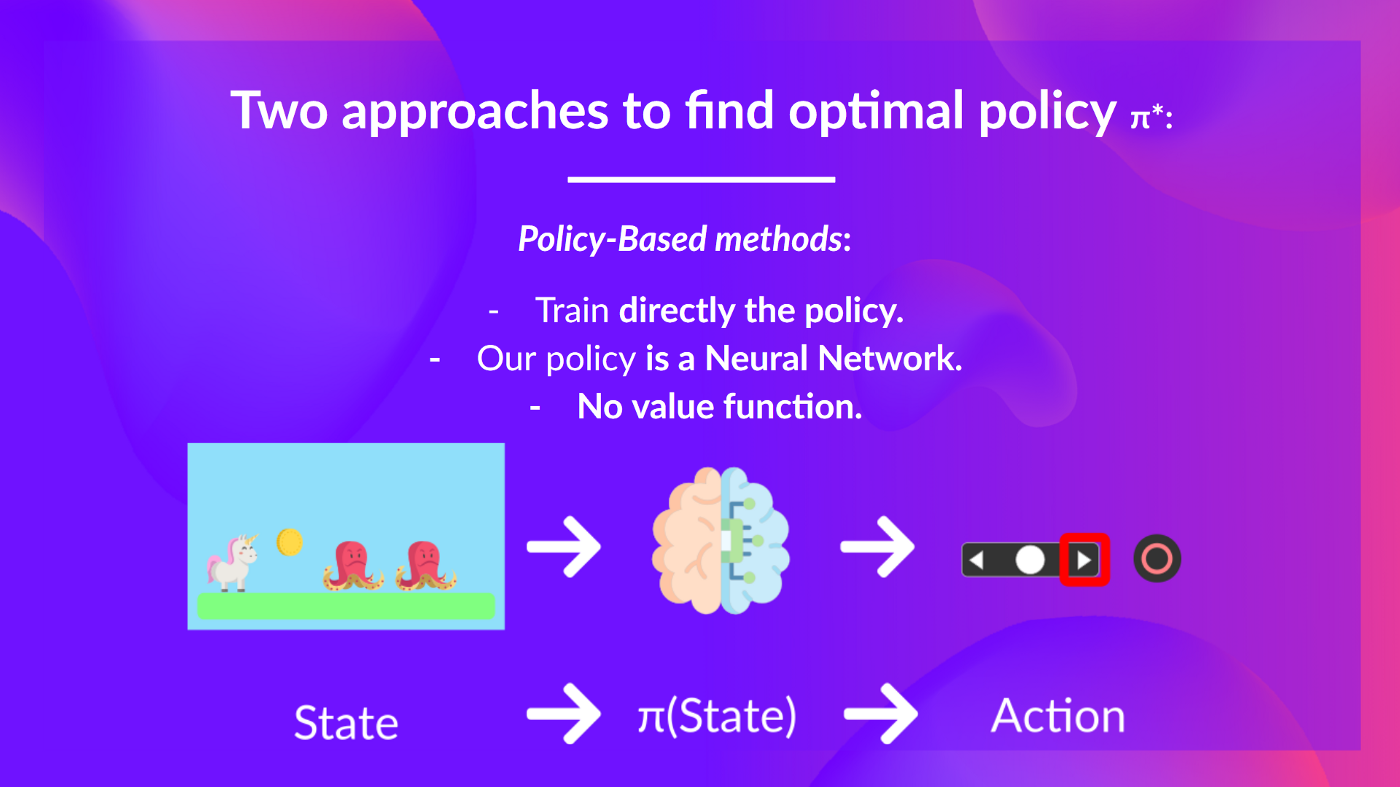
策略以状态作为输入,并输出在该状态下要采取的动作(确定性策略)。
因此,**我们不需要手动定义策略的行为;训练将定义它。**
- _基于价值的方法:_**间接地,通过训练一个价值函数**,该函数输出状态或状态-动作对的价值。给定此价值函数,我们的策略**将采取行动。**
但是,因为我们没有训练我们的策略,**我们需要指定其行为。**例如,如果我们需要一个策略,在给定价值函数的情况下,它将总是采取导致最大奖励的动作,**我们将创建一个贪婪策略。**

因此,无论您使用哪种方法解决问题,**您都会有一个策略**,但在基于价值的方法中,您不训练它,您的策略**只是一个您指定的简单函数**(例如贪婪策略),并且此策略**使用价值函数给出的值来选择其动作。**
所以区别在于:
- 在基于策略的方法中,**通过直接训练策略来找到最优策略。**
- 在基于价值的方法中,**找到一个最优价值函数会导致拥有一个最优策略。**

事实上,在大多数情况下,基于价值的方法会使用**一个 Epsilon-Greedy 策略**来处理探索/利用的权衡;我们将在本单元的第二部分讨论 Q-Learning 时详细说明。
所以,我们有两种基于价值的函数:
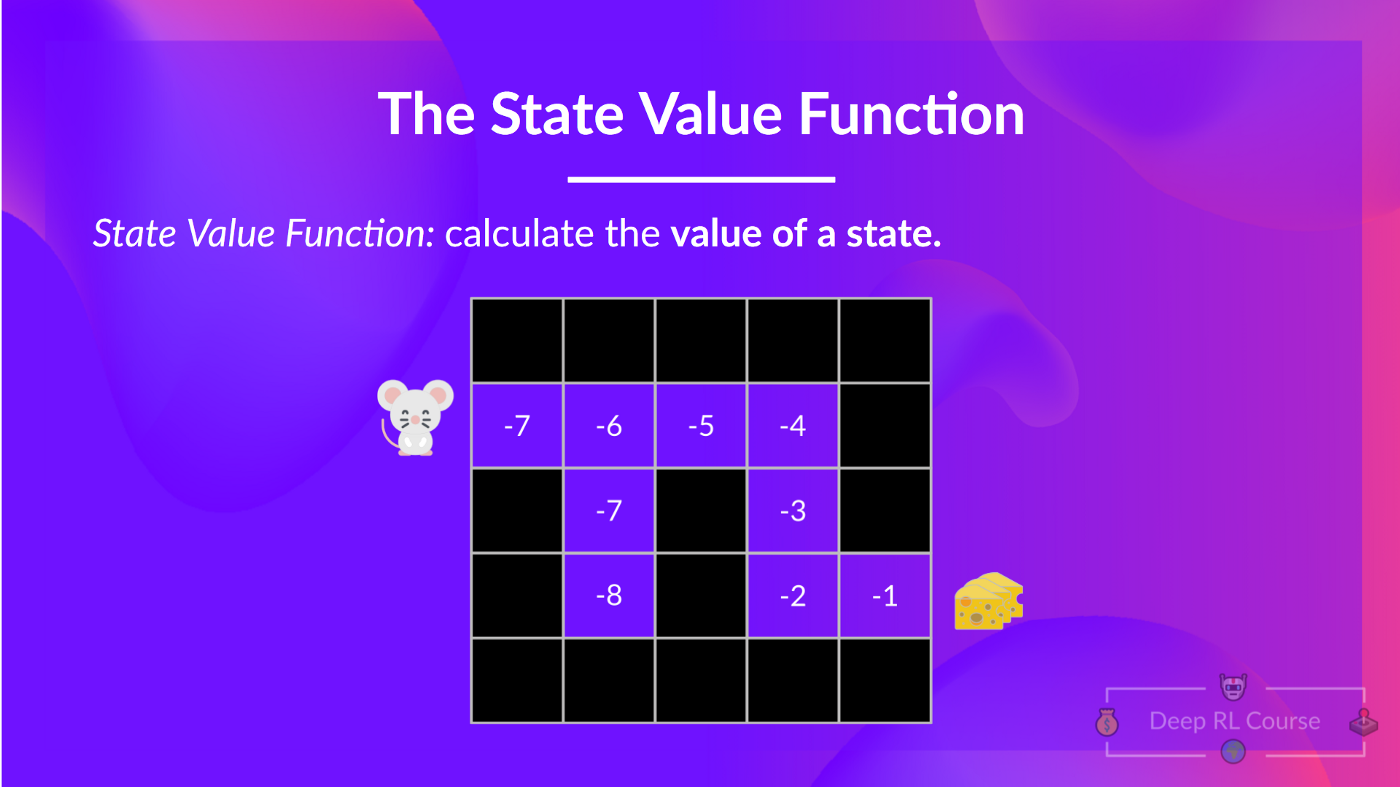
**状态价值函数**
我们这样写策略 π 下的状态价值函数:
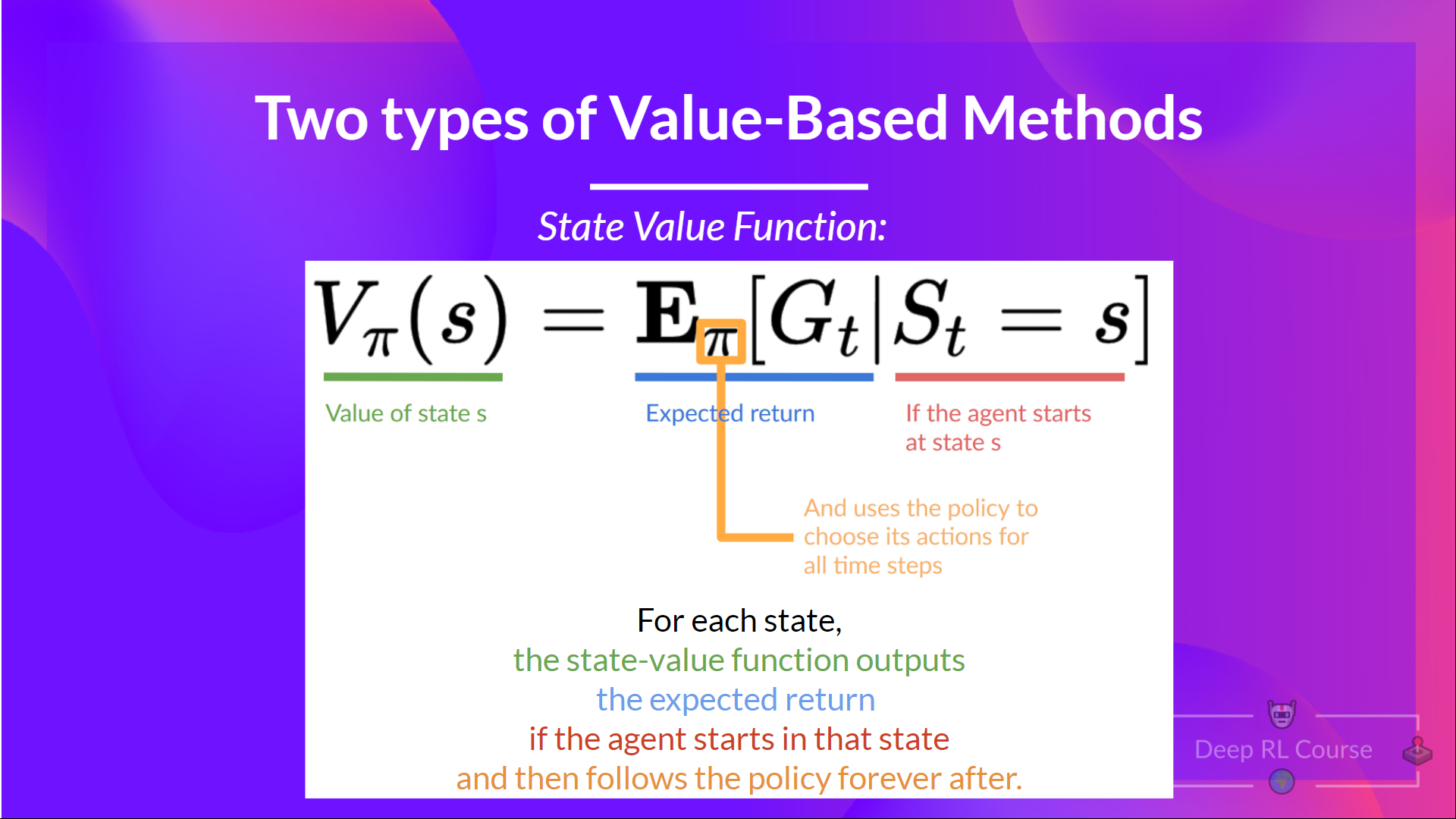
对于每个状态,状态价值函数输出预期回报,如果智能体**从该状态开始**,然后永远遵循该策略(如果你喜欢,对于所有未来的时间步)。
**动作价值函数**
在动作价值函数中,对于每个状态和动作对,动作价值函数输出预期回报,如果智能体从该状态开始并采取动作,然后永远遵循该策略。
在策略 π 下,在状态 s 采取动作 a 的价值是


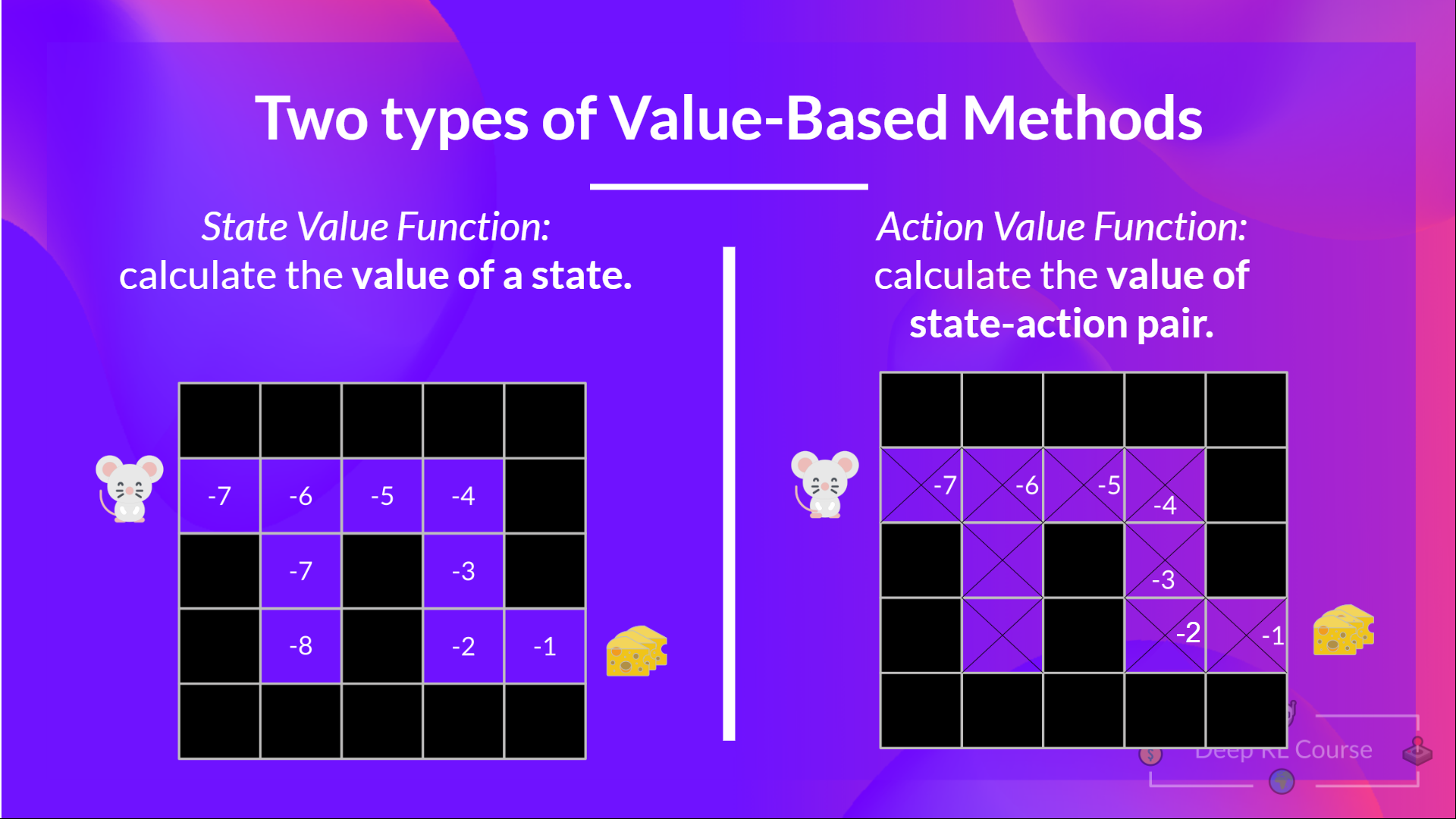
我们看到区别在于:
- 在状态价值函数中,我们计算**状态 **的价值。
- 在动作价值函数中,我们计算**状态-动作对( )的价值,因此是采取该动作在该状态下的价值。**
无论我们选择哪种价值函数(状态价值或动作价值函数),**价值都是预期回报。**
然而,问题在于,这意味着**要计算一个状态或一个状态-动作对的每个价值,我们需要对智能体从该状态开始可以获得的所有奖励进行求和。**
这可能是一个繁琐的过程,而这正是**贝尔曼方程帮助我们的地方。**
**贝尔曼方程:简化我们的价值估计**
贝尔曼方程**简化了我们的状态价值或状态-动作价值计算。**

根据我们目前所学,我们知道如果计算 (一个状态的价值),我们需要计算从该状态开始并永远遵循策略的回报。(**在以下示例中,我们定义的策略是贪婪策略,为了简化,我们不对奖励进行折扣**)。
因此,要计算 ,我们需要对预期奖励求和。因此:
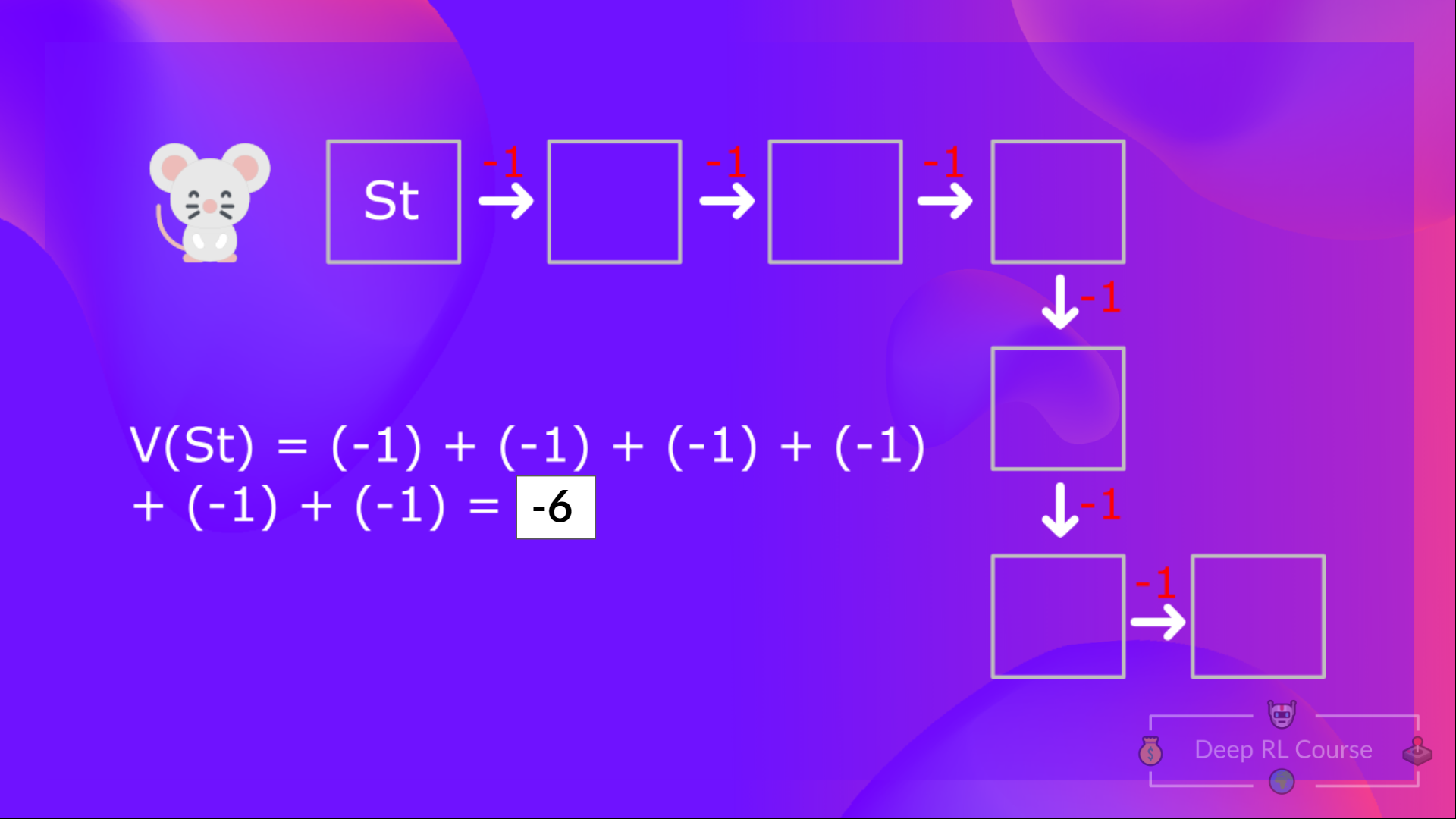
然后,要计算 ,我们需要计算从状态 开始的回报。
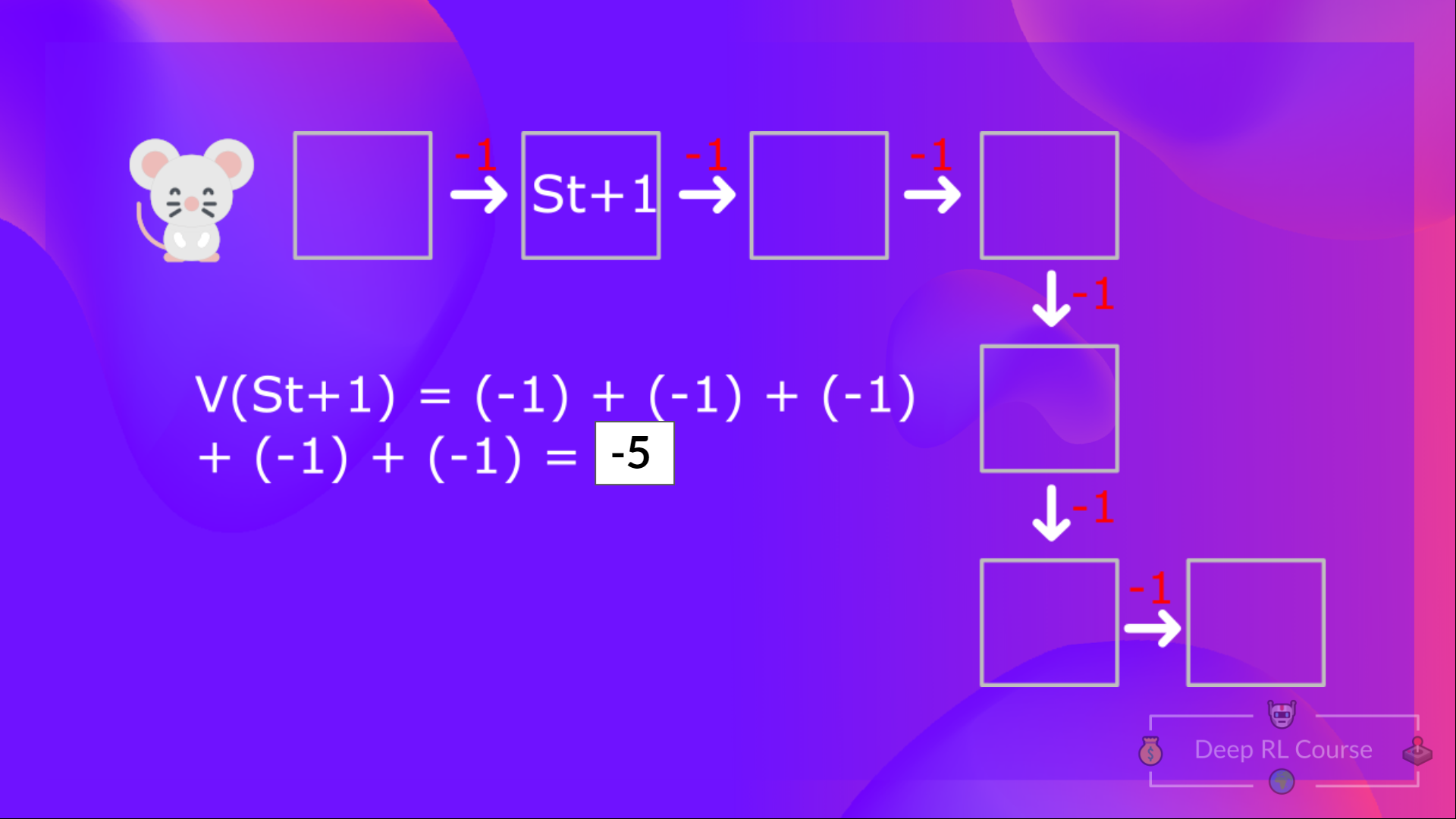
所以你看,如果你需要对每个状态值或状态-动作值都这样做,那将是一个非常繁琐的过程。
与其计算每个状态或每个状态-动作对的预期回报,**我们可以使用贝尔曼方程。**
贝尔曼方程是一个递归方程,其工作原理如下:我们不再从头开始计算每个状态的价值并计算回报,而是将任何状态的价值视为:
即时奖励 + 后续状态的折扣值( )。

如果回到我们的例子,状态 1 的价值 = 如果我们从该状态开始,预期的累积回报。

为了计算状态 1 的价值:**如果智能体从状态 1 开始**,然后**在所有时间步长中都遵循策略**,则奖励的总和。
这等价于 = 即时奖励 + 下一个状态的折扣值
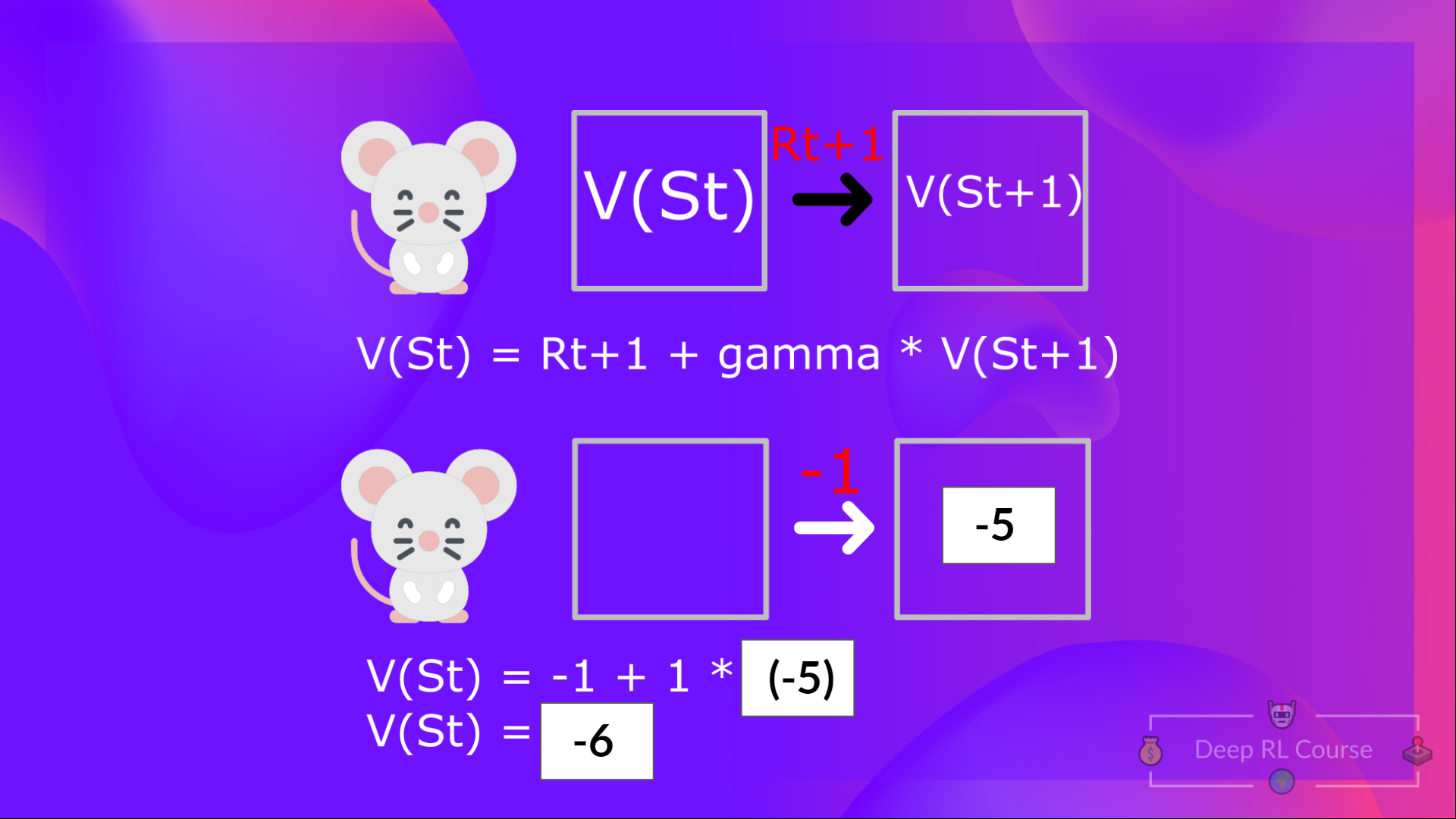
为简化起见,这里我们不打折,所以伽马 = 1。
- 的值 = 即时奖励 + 下一个状态的折扣值( )。
- 等等。
总结一下,贝尔曼方程的理念是,不再将每个值计算为预期回报的总和,**这是一个漫长的过程。**这等价于**即时奖励 + 下一个状态的折扣值的总和。**
**蒙特卡罗 vs. 时序差分学习**
在深入 Q-Learning 之前,我们需要谈论的最后一件事是两种学习方式。
请记住,RL 智能体**通过与环境交互来学习。**其理念是,**利用获得的经验**,根据获得的奖励,**更新其价值或策略。**
蒙特卡罗和时序差分学习是两种不同的**训练我们的价值函数或策略函数的方法。**它们都**利用经验来解决强化学习问题。**
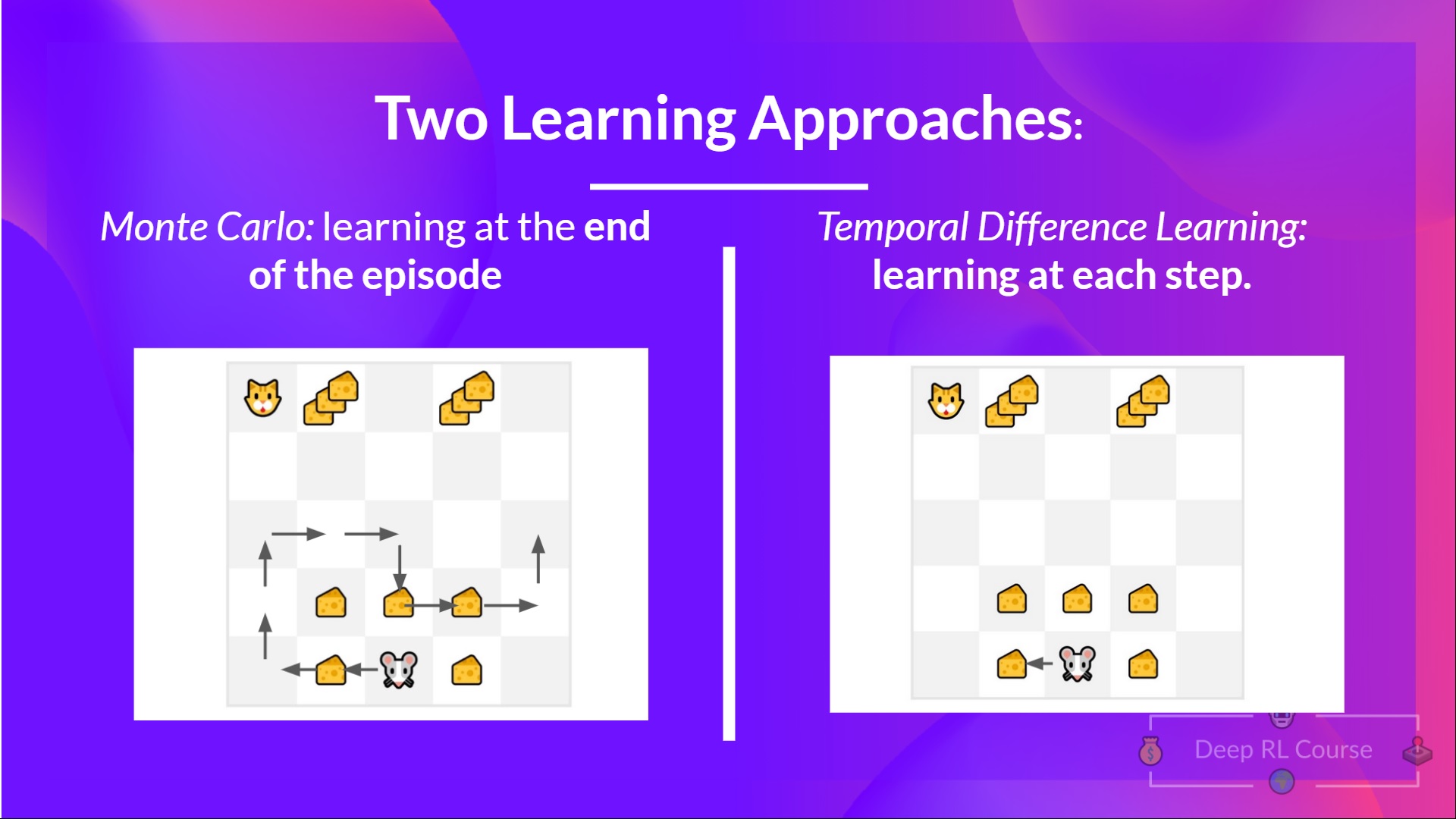
一方面,蒙特卡罗在学习之前使用**整个回合的经验。**另一方面,时序差分只使用**一个步骤( )来学习。**
我们将通过**一个基于价值的方法示例**来解释两者。
**蒙特卡罗:在回合结束时学习**
蒙特卡罗会等到回合结束,计算 (回报),并将其用作**更新 的目标。**
因此,它需要**一个完整的交互回合才能更新我们的价值函数。**

如果我们举一个例子:
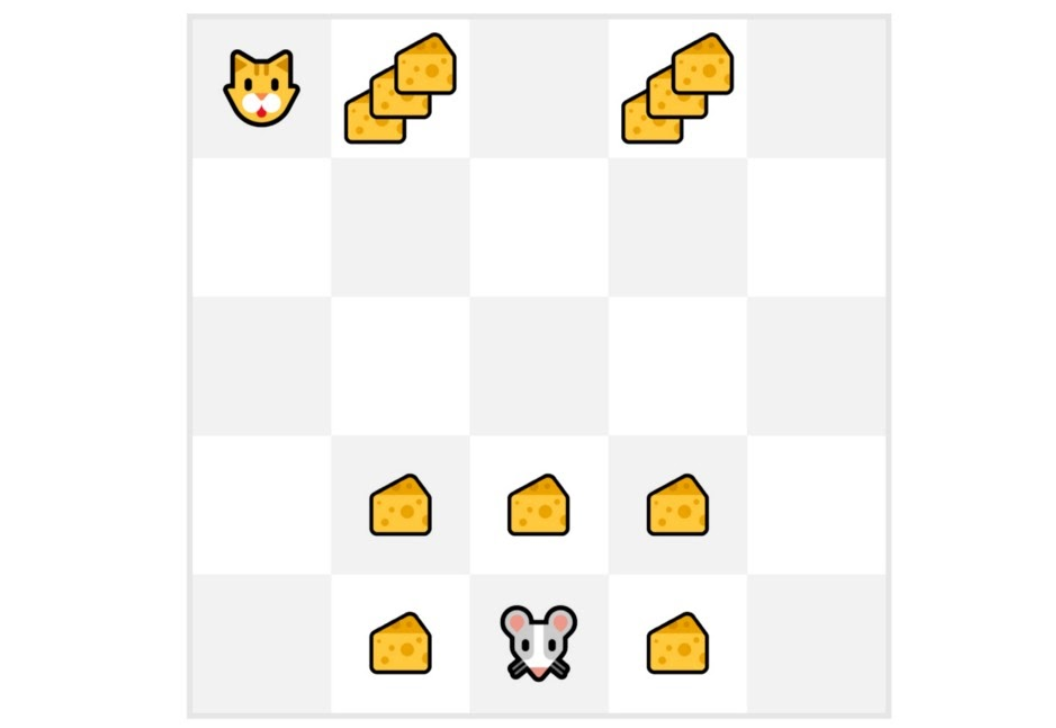
我们总是从**相同的起始点**开始一个回合。
**智能体使用策略采取行动**。例如,使用 Epsilon 贪婪策略,它在探索(随机行动)和利用之间交替。
我们得到**奖励和下一个状态。**
如果猫吃了老鼠,或者老鼠移动了 > 10 步,我们就终止这个回合。
在回合结束时,**我们有一个状态、动作、奖励和下一个状态的列表**。
**智能体将对总奖励 进行求和**(以查看其表现如何)。
然后它将**根据公式更新 **。

- 然后**带着这些新知识开始新的游戏。**
通过运行越来越多的回合,**智能体将学会玩得越来越好。**

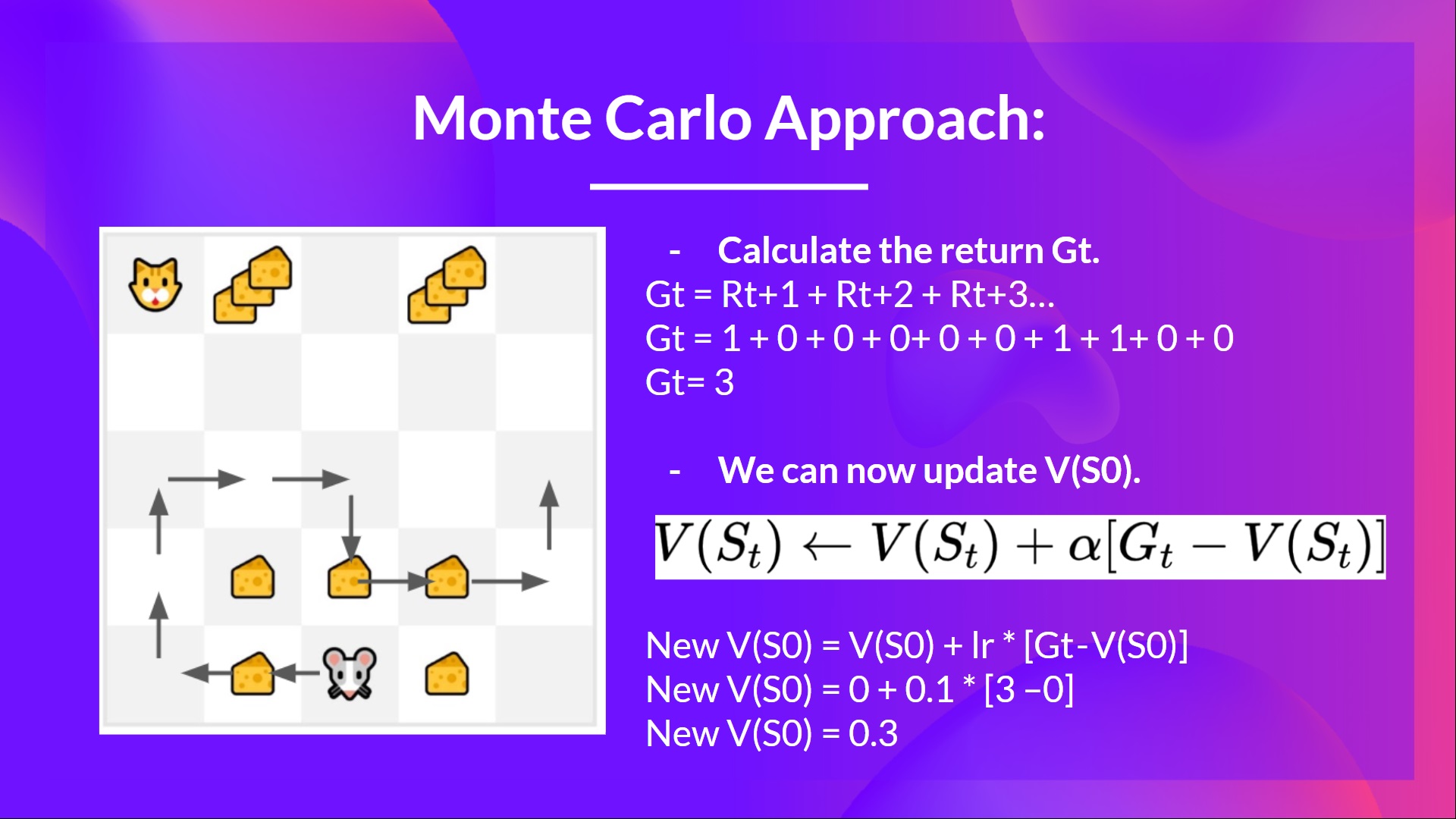
例如,如果我们使用蒙特卡罗训练一个状态价值函数:
- 我们刚刚开始训练我们的价值函数,**因此它对每个状态都返回 0 值。**
- 我们的学习率 (lr) 为 0.1,折扣率为 1(= 无折扣)。
- 我们的老鼠**探索环境并采取随机行动**。
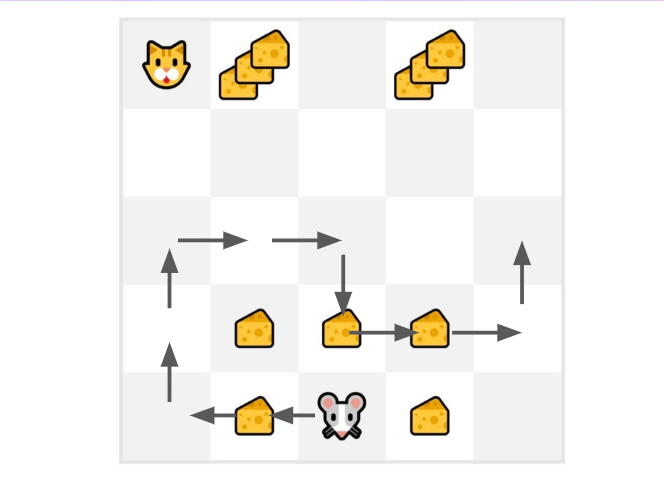
- 老鼠走了超过 10 步,所以回合结束了。
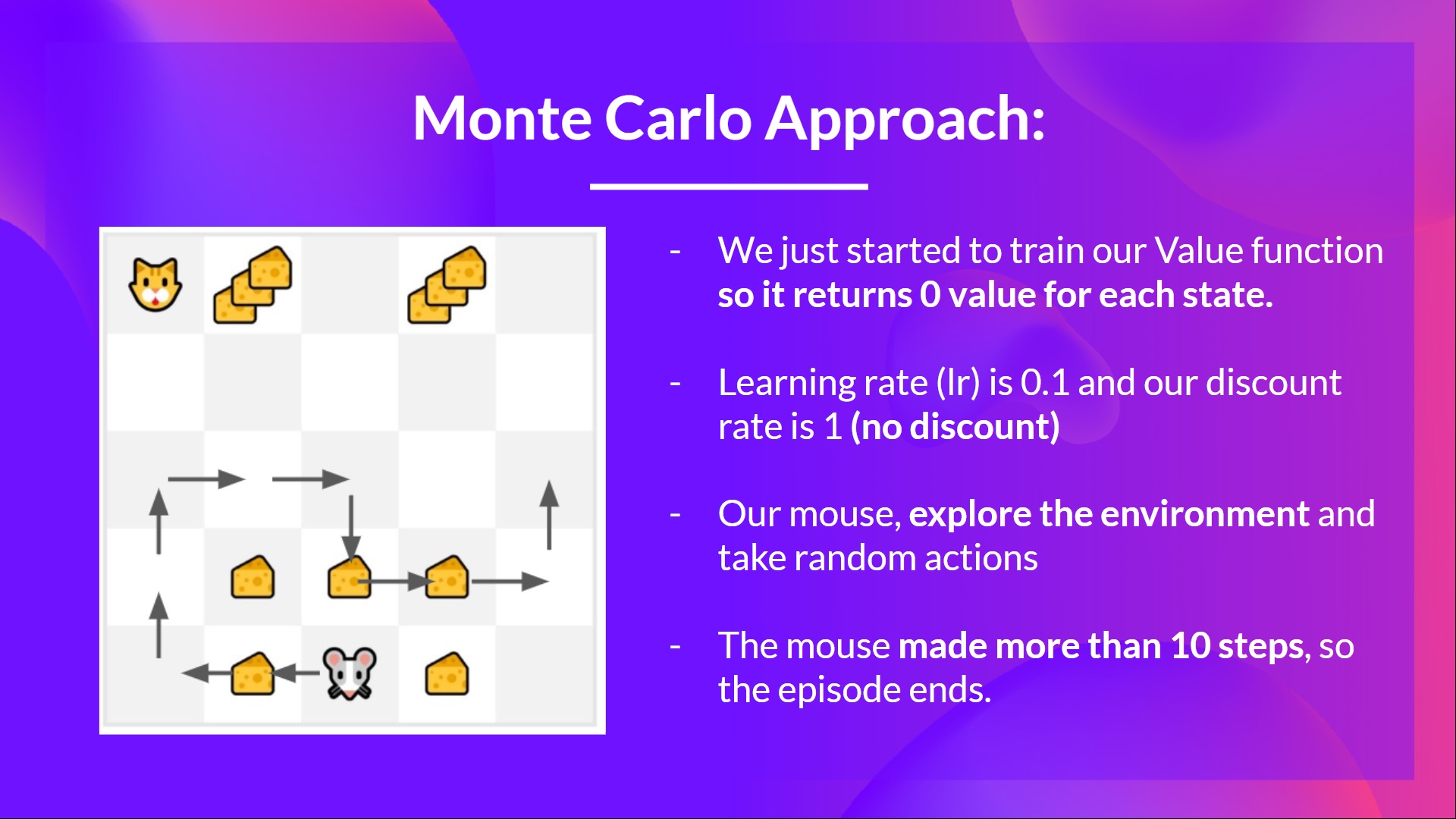
- 我们有一个状态、动作、奖励、下一个状态的列表,**我们需要计算回报 **。
- (为简单起见,我们不对奖励进行折扣)。
- 我们现在可以更新 了。

- 新的
- 新的
- 新的
**时序差分学习:在每一步学习**
- 另一方面,时序差分只等待一次交互(一个步骤)
- 以形成一个 TD 目标,并使用 和 来更新 。
TD 的核心思想是在每一步都更新 。
但由于我们没有在一个完整的 episode 中进行游戏,所以我们没有 (预期回报)。相反,我们通过将 和下一个状态的折扣值相加来估算 。
这被称为自举法。之所以这样命名,是因为 TD 更新部分是基于现有估计值 ,而不是完整的样本 。

此方法称为 TD(0) 或单步 TD(在任何单个步骤后更新值函数)。

如果我们采用相同的例子,

- 我们刚刚开始训练我们的值函数,所以它为每个状态返回 0 值。
- 我们的学习率(lr)是 0.1,我们的折扣率是 1(无折扣)。
- 我们的老鼠探索环境并采取了一个随机行动:向左走
- 它获得奖励 ,因为它吃到了一块奶酪。
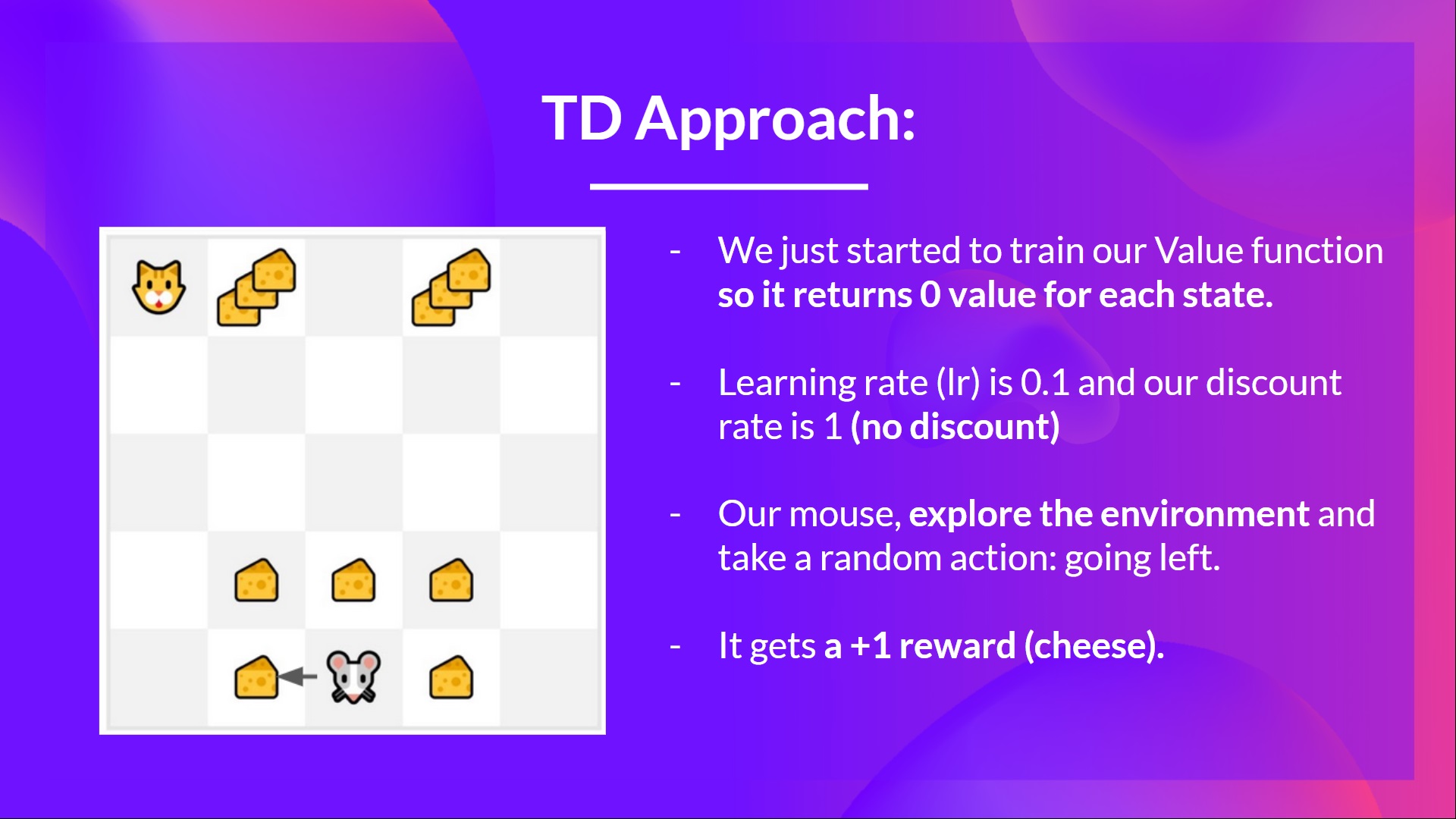
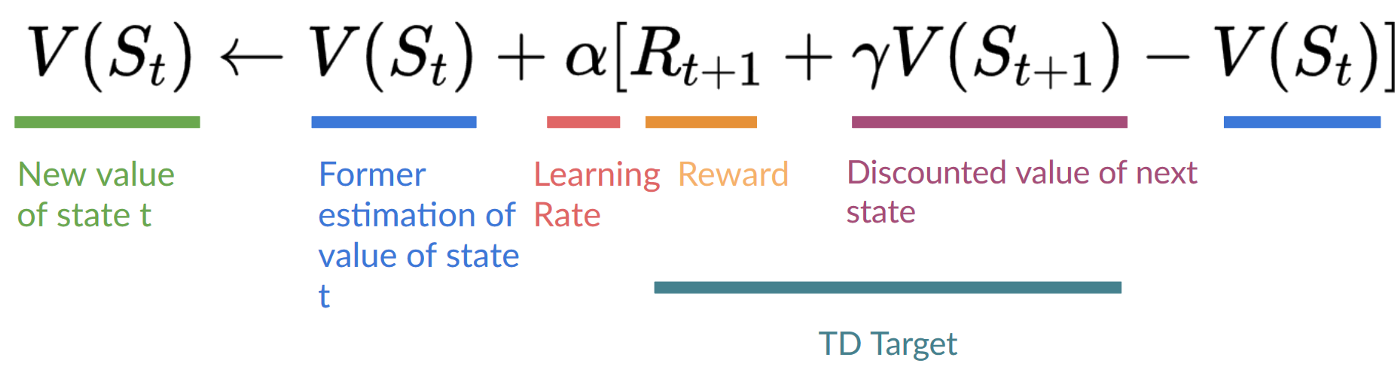
我们现在可以更新 了。
新
新
新
所以我们刚刚更新了状态 0 的值函数。
现在,我们将继续使用更新后的值函数与环境交互。

总结一下
- 使用蒙特卡洛方法,我们从一个完整的 episode 更新值函数,因此我们使用该 episode 实际准确的折扣回报。
- 使用 TD 学习,我们从一个步骤更新值函数,因此我们用称为 TD 目标的估计回报替换了我们没有的 。
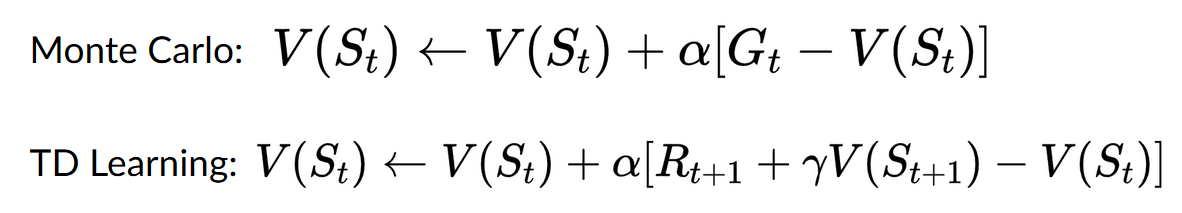
现在,在深入学习 Q-Learning 之前,让我们总结一下我们刚刚学到的内容
我们有两种类型的值函数
- 状态值函数:输出代理在给定状态开始并始终按照策略行动时的预期回报。
- 动作值函数:输出代理在给定状态开始,在该状态下采取给定动作,然后始终按照策略行动时的预期回报。
- 在基于值的方法中,我们手动定义策略,因为我们不训练策略,我们训练值函数。我们的想法是,如果我们有一个最优值函数,我们就会有一个最优策略。
有两种学习值函数策略的方法
- 使用蒙特卡洛方法,我们从一个完整的 episode 更新值函数,因此我们使用该 episode 实际准确的折扣回报。
- 使用TD 学习方法,我们从一个步骤更新值函数,因此我们用称为 TD 目标的估计回报替换了我们没有的 Gt。
今天就到这里。恭喜您完成本章的第一部分!信息量很大。
如果您仍然对所有这些内容感到困惑,这是正常的。我和所有学习强化学习的人都一样。
在继续之前,花时间真正理解这些材料.
由于学习和避免能力错觉的最佳方法是测试自己。我们编写了一个小测验来帮助您找到需要加强学习的地方。在这里查看您的知识 👉 https://github.com/huggingface/deep-rl-class/blob/main/unit2/quiz1.md
在第二部分中,我们将学习我们的第一个强化学习算法:Q-Learning,并在两个环境中实现我们的第一个强化学习代理。
- Frozen-Lake-v1(非滑溜版本):我们的智能体需要**从起始状态 (S) 到目标状态 (G)**,只在冰冻的瓷砖 (F) 上行走并避开洞 (H)。
- 一辆自动驾驶出租车需要**学习导航**城市,以**将其乘客从 A 点运送到 B 点。**

别忘了分享给你想学习的朋友 🤗!
最后,我们希望**根据你的反馈不断改进和更新课程**。如果你有任何反馈,请填写此表格 👉 https://forms.gle/3HgA7bEHwAmmLfwh9

