形状旋转101：Einsum和Jax Transformers简介

社区文章发布于2024年6月22日

Sankalp

dejavucoder

致谢

引言

Einsum是什么？

学习Einsum的三个理由

给我看看Einsum的例子

Einsum是如何工作的？

一些规则
张量收缩

所有元素的总和

迹

Einsum中的矩阵乘法

矩阵乘积转置

嵌套循环的观察

更多示例

关于Jax

简单Jax Transformer

前馈网络/MLP
Transformer块

注意力块

致谢

首先，我要感谢我的朋友和善意的网友们，他们为本文提供了帮助。

本文大量改编自以下内容：

非常感谢 _xjdr、Felix、Pushkar 和 Tokenbender 的校对。

引言

最近，我在成为一个“形状旋转者”的过程中，一直在“钻研”Jax和Einsum符号。

twirl

本文分为两部分。第一部分，我们介绍Einsum符号的基础知识。第二部分，我们将理解使用大量Einsum的Jax中简单Transformer代码。

从你们的角度，我需要一些大脑（不，我不是僵尸，我只是想吸引你们的注意力）。我还假设你们了解NumPy基础知识、矩阵乘法暴力算法和Transformer基础知识（仅限第二部分）。

如果我无法出色地解释Einsum，你们可以参考上面提到的文章2、3和4。2是PyTorch中的Einsum，它建立在3和4的基础上。3深入探讨内部原理，而4则侧重于带示例的符号。

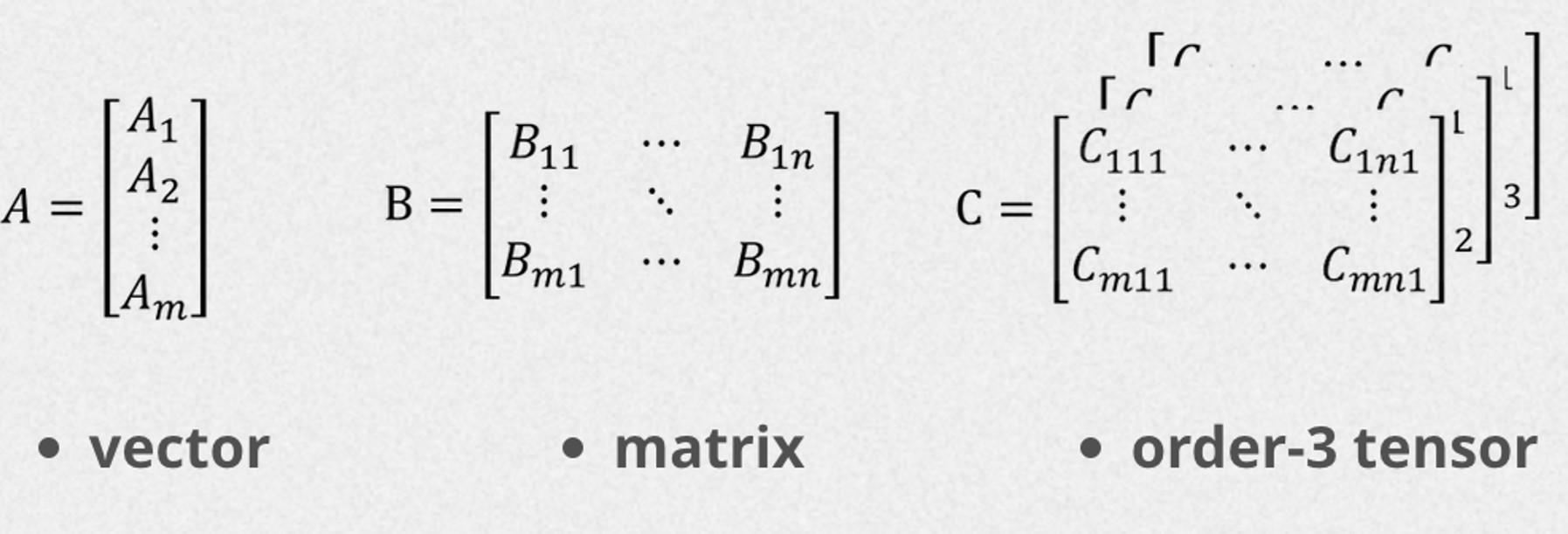
第一部分：如何使用einsum进行形状旋转

Einsum是什么？

Einsum是由多个库提供的一种用于张量/数值数组操作的替代API。NumPy（自v1.6起）、PyTorch和其他科学计算库都提供了`einsum`函数。

Einsum符号是由……你猜对了，阿尔伯特·爱因斯坦引入的 [维基百科]

该函数利用爱因斯坦求和记号来简化多维数组上复杂的线性代数运算——**张量收缩**（稍后详述）和求和。其语法在NumPy、Torch、Jax等库中基本一致。

numpy.einsum

`numpy.einsum(*subscripts, *operands, out=None, dtype=None, order='K', casting='safe', optimize=False)`[来源]

torch.einsum

`torch.einsum(equation, *operands) → [Tensor]` [来源]

学习einsum的三个理由

学习einsum值得你花时间。许多深度学习研究人员在他们的工作中都使用它。

成为真正的形状旋转器。

它可以通过其表达能力和智能循环，在速度和内存效率方面**超越熟悉的数组函数**。它也是自文档化的。唯一的缺点是其符号在初学时可能难以理解。

好的，给我看一个Einsum的例子

假设我们有两个矩阵 **A** 和 **B**，我们想要将它们 **逐元素相乘，然后对轴 = 1（按行）求和**

A = np.array([0, 1, 2]) # shape (3,)

B = np.array([[ 0,  1,  2,  3], # (3, 4)
              [ 4,  5,  6,  7],
              [ 8,  9, 10, 11]])

使用einsum符号表示，

>>> np.einsum('i,ij->i', A, B)
array([ 0, 22, 76])

如果没有einsum，它会是这样的：

将它们相乘。


>>> A * B
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
ValueError: operands could not be broadcast together with shapes (3,) (3,4)

但是，哎呀，我这个笨蛋忘记了重塑。你需要矩阵具有相同的维度才能进行广播。将A从(3,)转换为(3, 1)（本质上是一个列向量）

>>> A = A[:, np.newaxis]
>>> A
array([[0],
       [1],
       [2]])

现在你可以执行

>>> (A * B).sum(axis = 1)
array([ 0, 22, 76])

#  A gets broadcasted from (3, 1) to (3, 3) before multiplication
# [0 0 0]
# [1 1 1]
# [2 2 2]

重申一下，有了 einsum，你所**需要的**只是 **np.einsum('i,ij->i', A, B)**。

让我们试着理解它是如何工作的。

它是如何工作的

np.einsum('指定索引和操作的字符串', matrix1, matrix2 ...)

字符串看起来像`i, ij->i` —— `输入索引 -> 输出索引`

`i, ij` - 输入规范（我们对其进行操作的矩阵的维度/轴）。逗号分隔不同矩阵的索引。

`i` → 输出规范（所需形状）

**i** 对应矩阵A的行，**ij** 分别对应矩阵B的行和列。

字符串中可以使用哪些特定字母是任意的。你可以使用`a, ab->a`。只需确保每个矩阵的每个轴/维度都有一个标签/索引来表示即可。

每个字母/标签，例如 i, j，表示将要迭代的矩阵/张量的轴，可以表示为一组深度嵌套的for循环。你需要了解一些重要的规则，之后就很容易理解 einsum 了。

一些规则

[1] **输入数组之间重复的字母意味着沿着这些轴的值将相乘。乘积构成输出数组的值。**

i, ij->i

结果将是A和B逐元素相乘后，沿着轴=1（按行）求和，这意味着它将是一个行向量。

product[i] = A[i] * B[i,j]

如果我们的 einsum 是 `bmhk, bhlm -> blhk`，那么

product[b, l, h, k] = A[b, m, h, k] * B[b, h, l, m]

[2] **输出中省略一个字母意味着沿着该轴的值将被求和。**

简单来说，任何没有出现在字符串右侧的字母/索引都将被求和。我们不在RHS放置 **j**，因为我们希望沿着该维度（按列）进行求和。

`output[i] += A[i] * B[i, j]` # 这是一个张量收缩

张量收缩

这里稍作离题。我们刚才所做的就是张量收缩。

它将矩阵乘法的概念推广到更高维数组或张量。通过对两个张量之间配对索引的乘积进行求和，从而产生一个降维的新张量。这就是 **einsum 的作用。**

从数学上讲，上述操作可以表示为

$\begin{equation}\text{result}[i] = \sum_{j} A[i] \cdot B[i,j]\end{equation}$

对于 i 的每个值，A[i] 的元素将与 B[i,j] 沿着 j 轴的相应元素相乘。
乘积在 `j` 轴上求和，有效地降低了结果的维度。
结果张量的形状为 `[i]`，由输出索引指定。

下面是如果我们将上面的einsum写成嵌套for循环的形式（求和是针对最内层的for循环）的样子。


# for loop for above einsum
result = np.zeros(A.shape[0])
for i in range(A.shape[0]):
    for j in range(B.shape[1]):
        result[i] += A[i] * B[i, j]

但它为什么更快呢？它不需要重塑，从而避免了创建临时数组 `A[:, np.newaxis] * B` 的开销。它只是在计算过程中将乘积沿行求和。这是我们第一个示例的复杂解释。

[3] **我们可以按任何我们喜欢的顺序返回未求和的轴。**

这有点类似于重塑/重新排列。

例如，转置将是 `np.einsum('ij->ji', A)`

>>> A = np.array([[1, 2, 3],
...               [4, 5, 6],
...               [7, 8, 9]])
>>>
>>> # Perform transpose using einsum
>>> A_transpose = np.einsum('ij->ji', A)
>>> A_transpose
array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

所有元素的总和

np.einsum('ij->', A) - 省略i、j表示沿着这些维度进行求和。

# Perform summation using for loop
sum_loop = 0
for i in range(A.shape[0]):
    for j in range(A.shape[1]):
        sum_loop += A[i, j] * 1

迹

np.einsum(’ii->’, A) 用于矩阵的迹（对角线元素的和）

Einsum中的矩阵乘法

$C_{ij} = \sum_{k} A_{ik} B_{kj}$

更好地展示 einsum 的例子是矩阵乘法。上述运算可以通过三个嵌套的 for 循环（暴力矩阵乘法算法）表示。这里有一个动画。

k是重复的，这意味着乘积发生在k上。k不在输出规范求和中。k被称为**求和索引**。

Einsum 格式字符串中的所有索引都可以分为两组：自由索引和求和索引

*自由索引*是输出规范（字符串右侧）中使用的索引。它们与*外层* `for` 循环相关联。

*求和索引*是所有其他索引：它们出现在参数规范中，但**不**出现在输出规范中。它们之所以被称为求和索引，是因为在计算输出张量时它们会被*求和消除*。**它们与*内层* `for` 循环相关联。**

你也可以将矩阵乘法表示为 `np.einsum('ij,jk->ik', A, B)`，这仍然是有效的（正如我之前提到的，字母是任意的）。

矩阵乘积转置

假设你想得到矩阵乘积的转置，即 (A @ B).T

`np.einsum('ij,jk->ki', A, B)` 注意我们是如何将`ik`重新排列为`ki`，这就是一个转置。

嵌套循环的观察

`ij, jk->ik` - 字符串中唯一索引的数量 = 嵌套循环的数量

嵌套循环的顺序将遵循字符串右侧/输出规范的顺序。

右侧不存在的索引——求和索引，总是出现在最内层循环中

第二部分：解码简单的jax transformer

再次向 **xjdr 先生** 致敬，感谢他开源了 Jax Transformer 代码。

他编写的代码清晰且经过测试。他还解答了我的一些疑问。

关于Jax

Jax 介于 NumPy 和 PyTorch 之间。研究人员主要使用 PyTorch 进行研究，但对于生产负载，人们正转向 Jax，因为它更快。你会发现它的语法类似于 NumPy（但它非常强调函数式编程概念，如纯函数、不可变数组等）。它使用 JIT（即时编译）来加速。

接下来，我们将尝试解码Jax中这个简单的transformer实现。

简单的Jax Transformer

根据_xjdr先生的说法，“这是一个只有解码器的，来自早期noam时代（RoPE transformer之前）的transformer”

from typing import List, NamedTuple

import jax
import jax.numpy as jnp

class LayerWeights(NamedTuple):
  attn_norm: jax.Array
  ffn_norm: jax.Array
  w_q_dhk: jax.Array
  w_k_dhk: jax.Array
  w_v_dhk: jax.Array
  w_o_hkd: jax.Array
  w1: jax.Array
  w2: jax.Array
  w3: jax.Array

class XfmrWeights(NamedTuple):
  tok_embeddings: jax.Array
  layer_weights: List[LayerWeights]
  norm: jax.Array
  output: jax.Array

def norm(x, w, eps: float = 1e-6):
    return w * (x * jax.lax.rsqrt(jax.lax.pow(x, 2).mean(-1, keepdims=True) + eps))

def attention(input_bld, params):
    """
    B: batch size
    L: sequence length
    M: memory length 
    D: model dimension
    H: number of attention heads in a layer
    K: size of each attention key or value
    """
    normalized_bld = norm(input_bld, params.attn_norm)
    query_blhk = jnp.einsum('bld,dhk->blhk', normalized_bld, params.w_q_dhk)
    key_blhk = jnp.einsum('bld,dhk->blhk', normalized_bld, params.w_k_dhk)
    value_blhk = jnp.einsum('bld,dhk->blhk', normalized_bld, params.w_v_dhk)
    logits_bhlm = jnp.einsum('blhk,bmhk->bhlm', query_blhk, key_blhk)
    _, l, h, k = query_blhk.shape
    logits_bhlm = logits_bhlm / jnp.sqrt(k)
    mask = jnp.triu(jnp.ones((l, l)), k=1).astype(input_bld.dtype)
    logits_bhlm = logits_bhlm - jnp.inf * mask[None, None, :, :]
    weights_bhlm = jax.nn.softmax(logits_bhlm, axis=-1)
    wtd_values_blhk = jnp.einsum('blhk,bhlm->blhk', value_blhk, weights_bhlm)
    out_bld = jnp.einsum('blhk,hkd->bld', wtd_values_blhk, params.w_o_hkd)
    return out_bld

def ffn(x: jax.Array, w1: jax.Array, w2: jax.Array, w3: jax.Array) -> jax.Array:
  return jnp.dot(jax.nn.silu(jnp.dot(x, w1)) * jnp.dot(x, w3), w2)

def transformer(tokens: jax.Array, params: jax.Array) -> jax.Array:
  x = params.tok_embeddings[tokens]
  def scan_fn(h, layer_weights):
    h += attention(h, layer_weights)
    h += ffn(norm(h, layer_weights.ffn_norm), layer_weights.w1, layer_weights.w2, layer_weights.w3)
    return h, None
  h, _ = jax.lax.scan(scan_fn, x, params.layer_weights)
  h = norm(h, params.norm)
  logits = jnp.dot(h, params.output.T)
  return logits

if __name__ == '__main__':
  vocab_size = 32000
  dim = 4096
  hidden_dim = 14336
  n_layers = 1
  n_heads = 32
  head_dim = dim // n_heads

  layer_weights = LayerWeights(
      attn_norm=jnp.ones((n_layers, dim,)),
      ffn_norm=jnp.ones((n_layers, dim,)),
      w_q_dhk=jnp.zeros((n_layers, dim, n_heads, head_dim)),
      w_k_dhk=jnp.zeros((n_layers, dim, n_heads, head_dim)),
      w_v_dhk=jnp.zeros((n_layers, dim, n_heads, head_dim)),
      w_o_hkd=jnp.zeros((n_layers, n_heads, head_dim, dim)),
      w1=jnp.zeros((n_layers, dim, hidden_dim)),
      w2=jnp.zeros((n_layers, hidden_dim, dim)),
      w3=jnp.zeros((n_layers, dim, hidden_dim))
    )
  params = XfmrWeights(tok_embeddings=jnp.ones((vocab_size, dim)), layer_weights=layer_weights, norm=jnp.ones((dim,)), output=jnp.ones((vocab_size, dim)))
  tokens = jnp.array([[123,234,234,345,446]])
  out = transformer(tokens, params)
  print(f'{out.shape=}')

让我们首先看最简单的——>FFN，然后自顶向下地处理transformer块，最后深入到多头注意力块（大量的einsum，但没什么好怕的）

前馈网络 / MLP

def ffn(x: jax.Array, w1: jax.Array, w2: jax.Array, w3: jax.Array) -> jax.Array:
  return jnp.dot(jax.nn.silu(jnp.dot(x, w1)) * jnp.dot(x, w3), w2)

$\text{FFN}(x, W_1, W_2, W_3) = \left(\text{SiLU}(x W_1) \odot (x W_3)\right) W_2$

Transformer层通常在注意力块之后有前馈网络，以增加非线性并捕获注意力头学习到的信息。这个MLP有两层线性变换和一个SiLU激活函数。

两个并行线性变换：`dot(x, W1)` 和 `dot(x, W3)`
对 `dot(x, W1)` 应用 SiLU 激活函数
将步骤2的结果与 `dot(x, W3)` 进行逐元素相乘
最终线性变换：步骤3的结果与W2的点积

Transformer块

在我们进入 Transformer 块之前，我想谈谈 `jax.lax.scan` 函数。

当您有一个for循环，在每一步中更新一个值，并希望返回最终结果以及每一步中的所有中间值（np.stack）时，您可以使用`jax.lax.scan`。在底层，它可以展开循环（并进行一些JIT操作）以加速。另一个目的是将scan_fn表达为纯函数（避免可变状态）。

from jax import lax

def cumulative_sum(accumulated_sum, current_element):
    """
    - `accumulated_sum`: The accumulated sum from the previous loop iteration.
    - `current_element`: The current array element being processed.
    """
    new_sum = accumulated_sum + current_element
    return new_sum, new_sum  # ("carryover", "accumulated")

initial_sum = 0
final_sum, cumulative_sums = lax.scan(cumulative_sum, initial_sum, array)

在Transformer中，我们需要多次应用相同的操作（注意力和前馈），每层一次。这就是`jax.lax.scan`派上用场的地方。

我们不需要编写循环来应用这些操作，而是可以使用 `scan` 更有效地完成。我们用它来重复编写（多头注意力+FFN）块。

所示的 transformer 函数是一个仅解码器的实现（因果掩码是提示）。没有位置编码。

Untitled 2

def transformer(tokens: jax.Array, params: jax.Array) -> jax.Array:
  x = params.tok_embeddings[tokens]
  def scan_fn(h, layer_weights):
    h += attention(h, layer_weights)
    h += ffn(norm(h, layer_weights.ffn_norm), layer_weights.w1, layer_weights.w2, layer_weights.w3)
    return h, None
  h, _ = jax.lax.scan(scan_fn, x, params.layer_weights)
  h = norm(h, params.norm)
  logits = jnp.dot(h, params.output.T)
  return logits

h += attention(h, layer_weights)
h += ffn(norm(h, layer_weights.ffn_norm), layer_weights.w1, layer_weights.w2, layer_weights.w3)

这些是残差连接，您也可以在图中看到。我们正在收集每个隐藏层的输出

下一节，我们将在“注意力就是你所需要的一切”之后，深入探讨注意力块。

注意力就是你所需要的一切 pic.twitter.com/pL5spdO1SY
— sankalp (@dejavucoder) 2023年12月20日

注意力块

Untitled 3

注意力是Transformer的核心，它允许模型识别输入中需要关注的部分。在本节中，我们将探讨多头注意力块的实现。

单头注意力：在单头注意力中，`h = 1`。

在深入了解完整的注意力实现之前，我们先花一点时间回顾一下这里常见的einsum。为了理解创建查询矩阵所涉及的einsum。我们将输入投影到单个注意力空间。

query_blk = jnp.einsum('bld, dk -> blk', normalized_bld, params.w_q_dk)

这里，'b'是批量大小，'l'是序列长度，'d'是模型维度，'k'是查询/键维度（潜在键空间）。`normalized_bld`是输入，`params.w_q_dk`是可学习权重。

注意：q 中的元素指的是计算注意力的标记，k（潜在空间）中的元素指的是可以被关注的标记。

上述einsum本质上是每个token的嵌入与一组学习权重向量之间的矩阵乘法/点积。`ld, dk -> lk`

更正式地说，这种投影将每个token的表示从'd'维转换为'k'维。这里，'h'，即头部数量，为1。

多头注意力：然而，我们在实现中使用的是多头注意力。你可以把它看作是单头注意力重复了h次。

老实说，我并不完全清楚为什么我们要对 `d` 求和。xjdr 先生说，可以把它想象成“对于这些标记嵌入中的每一个，告诉我你对它们了解多少，每个注意力头，在维度为 dim 的潜在空间中”。

如果单头注意力是通过一个镜头观察场景，那么多头注意力就是通过多个镜头观察同一个场景，每个镜头都有不同的视角。

query_blhk = jnp.einsum('bld, dhk -> blhk', normalized_bld, params.w_q_dhk)

请注意，这只是又一次矩阵乘法，增加了一个额外维度 (h)，其中求和发生在 d 轴上。现在我们将输入投影到 h 个注意力子空间中。

现在让我们看看完整的多头注意力块。

下面是缩放点积注意力方程。这是为h个头计算的（因此是多头）。

def attention(input_bld, params):
    """
    Implements multi-head self-attention mechanism.
    
    B: batch size
    L: sequence length
    M: memory length (same as L for self-attention)
    D: model dimension
    H: number of attention heads in a layer
    K: size of each attention key or value
    """
    
    # Layer normalization
    normalized_bld = norm(input_bld, params.attn_norm)
    
    # Linear projections to obtain query, key, and value
    # Notice they are just matrix multiplications with an extra batch dim
    # XWq operation
    query_blhk = jnp.einsum('bld,dhk->blhk', normalized_bld, params.w_q_dhk)
    # XWk operation
    key_blhk = jnp.einsum('bld,dhk->blhk', normalized_bld, params.w_k_dhk)
    # XWv operation
    value_blhk = jnp.einsum('bld,dhk->blhk', normalized_bld, params.w_v_dhk)
    
    # Compute attention scores (dot product of queries and keys)
    # Notice that keys don't have sequence length, they have memory length
    # Memory is the length of context model can attend to
    # i.e how many previous tokens it can refer to
    logits_bhlm = jnp.einsum('blhk,bmhk->bhlm', query_blhk, key_blhk)
    
    
    # Get shape for scaling
    _, l, h, k = query_blhk.shape
    
    # Scale dot products by sqrt(d_k)
    logits_bhlm = logits_bhlm / jnp.sqrt(k)
    
    
    # Create causal mask to prevent attending future tokens
    # causal mask (lower triangular)
    mask = jnp.triu(jnp.ones((l, l)), k=1).astype(input_bld.dtype)
    
    # Apply mask (set upper triangular region to -inf)
    logits_bhlm = logits_bhlm - jnp.inf * mask[None, None, :, :]
    
    # Apply softmax to get attention weights
    weights_bhlm = jax.nn.softmax(logits_bhlm, axis=-1)
    
    # Compute weighted sum of values
    wtd_values_blhk = jnp.einsum('blhk,bhlm->blhk', value_blhk, weights_bhlm)
    
    # Final linear projection
    out_bld = jnp.einsum('blhk,hkd->bld', wtd_values_blhk, params.w_o_hkd)
    
    return out_bld

为什么在 `logits_bhlm = jnp.einsum('blhk,bmhk->bhlm', query_blhk, key_blhk)` 中对 k 求和？因为 k 包含关于每个头中要关注哪个 token 嵌入的信息，这就是我们沿着该轴收集信息的原因。

我希望你对einsum有了更好的理解，并且对transformers和jax有了更多的了解。**如果你喜欢，请点赞并分享。**

我也在**寻找 GenAI (LLMs) 相关职位**，最好是在 B 轮或以上融资的初创公司（印度或美国/欧盟远程职位）。如果你有这方面的需求，请在 Twitter 上给我发私信，或者发送“你好”到 hgirl3078@gmail.com。我的背景是在一家中型美国金融科技公司拥有大约两年后端/通用软件工程生产经验。我还涉足过深度学习（大学时期）和应用 LLMs（最近）。

社区

通过拖放到文本输入框、粘贴或点击此处上传图片、音频和视频。

点击或粘贴此处以上传图片

· 注册或登录以评论